经典场驱动对量子系统生存概率的影响*
2019-12-16胡要花吴琴
胡要花 吴琴
1) (洛阳师范学院物理与电子信息学院,洛阳 471022)
2) (广东医科大学信息工程学院,东莞 523808)
考虑一个受经典场驱动的二能级系统与零温玻色子库相互作用,研究经典场驱动对量子Zeno效应和量子反Zeno效应中量子系统存活概率的影响.结果表明,经典场驱动可以降低量子系统的有效衰减率,即提高量子系统的存活概率.此外,环境的欧姆性对于提高量子系统的存活概率也起着重要作用,设置适当的环境欧姆参数可降低量子系统的有效衰减率.再者,随着二能级系统与经典场之间失谐量的增加,量子系统的存活概率降低,而通过增加经典场驱动的强度或选择合适的环境欧姆参数,可以抑制失谐带来的负面影响.
1 引 言
如果频繁地对一个不稳定的量子系统进行量子测量,那么这个量子系统的衰减速度会变得很慢,这种效应被称为量子Zeno效应.近年来的研究表明,量子Zeno效应在量子信息处理的各种任务中起着重要的作用.例如,它可以用来抑制耗散谐振器中纠缠的衰减[1],阻止量子腔中光场的相干演化[2],抑制开放量子系统中的退相干[3],实现单个光子的投影测量方案[4],抑制光学腔中驱动三能级系统的自发辐射[5],实现无物理粒子实际传输的直接通信[6],提高参数估计的精度[7]等.另一方面,如果量子测量的频率不够高,即测量的时间间隔过长,那么量子系统的衰减会加快,这就是量子反Zeno效应.实验上,量子Zeno效应和量子反Zeno效应在许多不同的物理装置中都被证实[8-12],而且它们在量子信息学中有着重要的潜在应用价值,因此吸引了研究者们的广泛兴趣[13-24].
最近的研究[25]证明遭受频繁重复测量的量子系统的有效寿命取决于环境的谱密度、系统-环境耦合以及所执行的测量.因此,在频繁重复测量的作用下,如何延长量子系统的生存时间,是一个值得研究的问题.随后,有研究者提出利用投影测量和幺正运算相结合,有效地抑制量子系统衰减的方案[26].本文提出应用经典场驱动来延长重复测量下量子系统生存概率的方案.经典场驱动在量子信息处理中发挥着极其重要的作用,比如,借助经典场驱动,可以提高量子系统的纠缠度、控制纠缠猝死的时间[27],抑制漏腔中量子相干和纠缠的衰减[28,29],加快与零温结构库耦合的量子比特的演化速度[30].此外,经典场驱动与非马尔可夫记忆效应的协同作用,可以提高噪声环境下参数估计的精度[31].在以上研究工作的启发下,本文考虑一个由经典场驱动的二能级系统与一个零温玻色子库相互作用,研究量子Zeno效应和量子反Zeno效应,并讨论经典场驱动对量子系统生存概率的影响.
2 有效衰减率
考虑一个二能级系统与玻色子环境相互作用.二能级系统的哈密顿量为 HS,玻色子环境的哈密顿量为 HB,系统与环境作用的哈密顿量用 V表示,则系统-环境整体的哈密顿量可以表示为
假设二能级系统初始状态为 |ψ〉.根据文献[25]提出的方法,经过重复投影测量后量子系统的生存概率为

式中,N是投影测量重复的次数,τ是两次测量之间的时间间隔.显然,1/Γ(τ) 表示量子系统的有效生存时间,Γ(τ) 则代表量子系统的有效衰减率.量子Zeno效应和量子反Zeno效应可由衰减率Γ(τ)随测量间隔 τ的变化确定:如果 Γ(τ) 随 τ的增大而增大,即发生了量子Zeno效应;若 Γ(τ) 随 τ的增大而减小即为量子反Zeno效应.当量子系统与环境弱耦合时,有效衰减率 Γ(τ) 可以表示为[25]

式中 J(ω) 是环境的谱密度函数.假设∑系统与环境耦合的哈密顿量 V可以表示为 V=μFμ⊗Bμ,则(3)式中的滤波函数 Q(ω,τ) 为
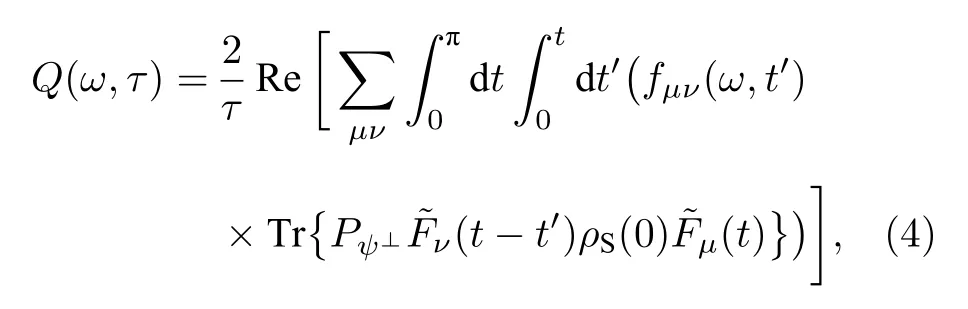
其中,ρS(0) 是二能级系统初始的密度矩阵,是与初态 |ψ〉正交的投影算符;函数由环境关联函数决定.环境关联函数定义为

3 模 型
考虑一个频率为 ω0的二能级系统,与零温玻色子环境相互作用,同时受频率为 ωL的经典场驱动.在旋转波近似下,系统-环境整体的哈密顿量可以写成
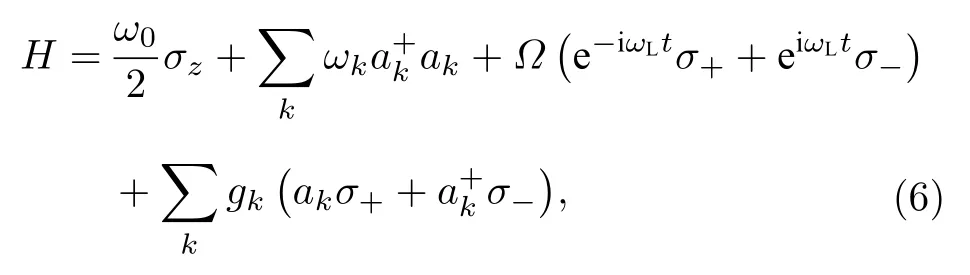
其中,σx,y,z是泡利算符;而 σ±是原子反转算符;分别是环境第k 个模式的频率、产生(湮灭)算符;拉比频率 Ω为实数,表示二能级系统与经典场之间的耦合;gk代表系统与环境第k 个模式耦合的常数.
作么正变换 UR=exp(-iωLσzt /2) ,可将(6)式所表示的哈密顿量转换成如下形式:

其中 Δ=|ω0-ωL|是二能级系统与经典驱动场作用的频率失谐.定义进一步将(7)式表示为
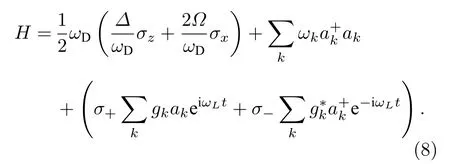
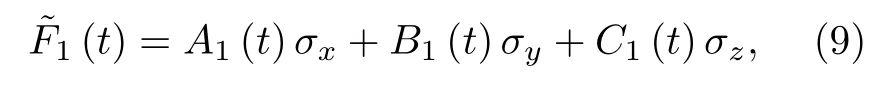
式中
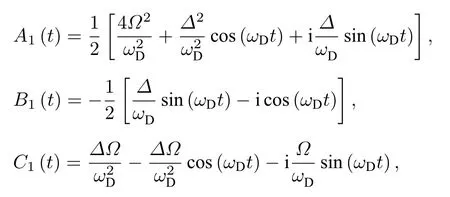
而
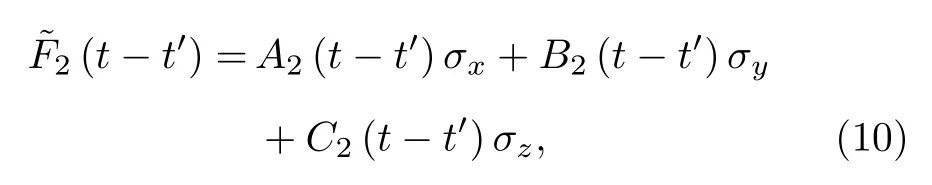
式中
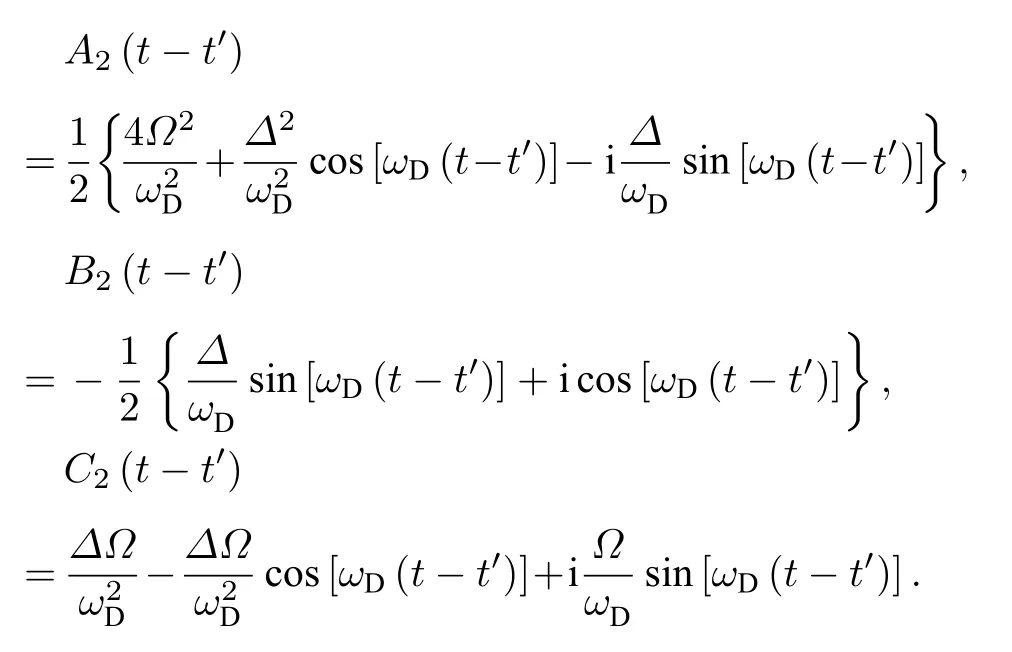
假设二能级系统的初态为

将以上这些结果代入(12)式,经过复杂的计算之后可得滤波函数
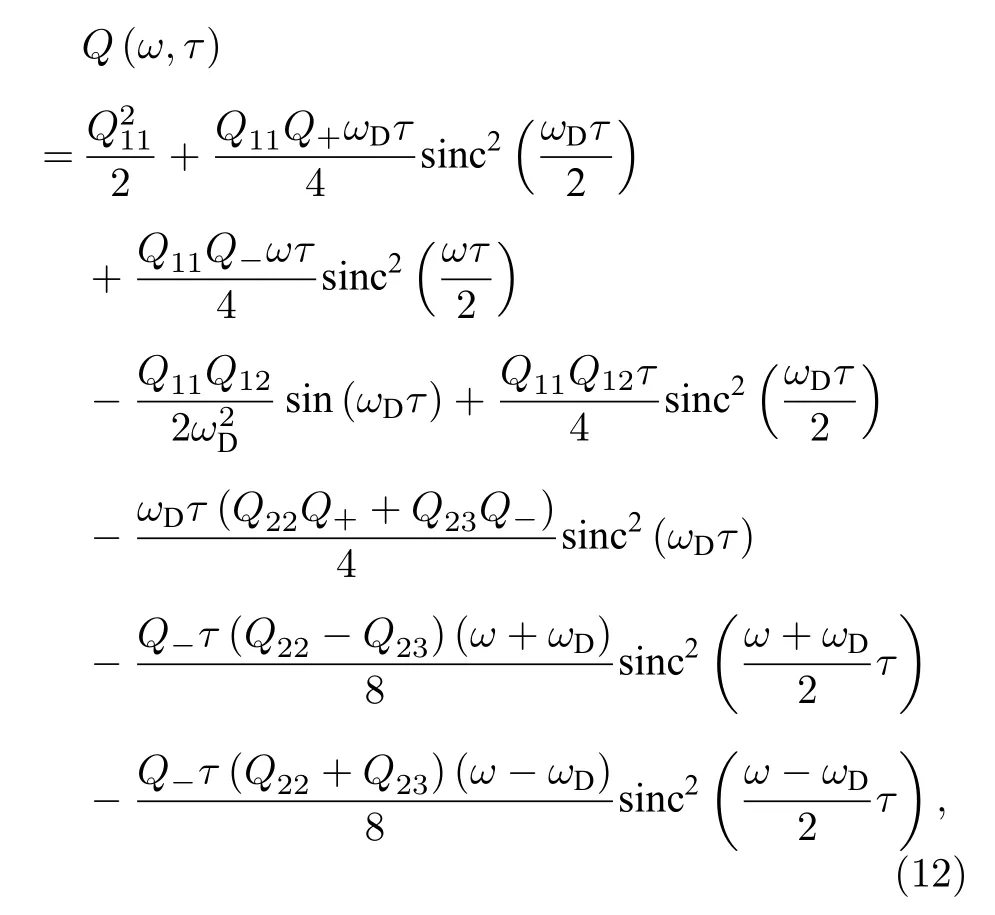
式中

4 量子Zeno效应和量子反Zeno效应
根据上一节的计算结果,分别展示共振和非共振条件下有效衰减率随测量间隔的变化(图1和图2).此外,也讨论了二能级系统初始处于非叠加态时的情形(图3).
图1展示了共振(Δ=0)条件下,参数G=0.01,ωc=10 时经典场驱动对有效衰减率的影响.其中,(a),(b),(c)分别代表参数 s 取0.5,1.0,2.0时有效衰减率随测量间隔的变化,而点虚线、虚线、实线分别代表经典驱动强度 Ω取0,30,50的情形.从图1可以看出:当测量间隔 τ很小时,衰减率 Γ(τ) 随 τ增大而增大,即出现量子Zeno效应;而当测量间隔 τ足够大时,Γ(τ) 随 τ增大而减小,即发生了量子反Zeno效应.此外,通过对比图1(a)和图1(b)中的实线、虚线和点虚线,发现拉比频率Ω值越大,有效衰减率 Γ(τ) 越小,也就是说,量子系统的生存概率越高.这一结果表明,对于欧姆和亚欧姆环境,经典场驱动可以提高量子系统在量子Zeno和反Zeno效应下的生存概率.因为当经典场驱动增强时,二能级系统与环境之间的有效耦合减弱,这有助于保持二能级系统处于初始状态.超欧姆环境下的情况稍有不同,对于较长的测量间隔,Ω=30 时的有效衰减率比 Ω=0 的大,如图1(c)所示.但进一步考虑拉比频率,如 Ω=50 时,Γ(τ)仍然很小.这一结果表明,有效衰减率不仅受到经典驱动强度的影响,而且还受到环境欧姆性的制约.对于 Ω=0 ,由图1中所有点虚线可以看出:当测量间隔很小时,欧姆环境中有效衰减率的值比超欧姆和亚欧姆环境中的值小;但当测量间隔很大时,超欧姆环境中的有效衰减率最小.对于 Ω/=0 ,亚欧姆环境中的 Γ(τ) 值总是小于欧姆环境和超欧姆环境中的 Γ(τ) 值.这些结果表明,可以通过选择适当的环境欧姆系数和经典驱动的强度来提高量子系统的生存概率.

图1 有效衰减率随测量间隔的变化曲线 (a) s =0.5;(b) s =1;(c)s =2Fig.1.The behavior of the effective decay rate as a function of the measurement interval:(a) s =0.5;(b) s =1;(c) s =2.

图2 有效衰减率随测量间隔的变化曲线 (a) Ω=30 ,s =0.5;(b) Ω=30 ,s =2;(c) Ω=50 ,s =2Fig.2.The beehavior of the effective decay rate as a function of the measurement interval:(a) Ω=30 ,s =0.5;(b) Ω=30 ,s =2;(c) Ω=50 ,s =2.
非共振(即 Δ/=0)条件下经典驱动强度和欧姆环境对有效衰减率的影响如图2所示.图2展示了 G=0.01 ,ωc=10 时有效衰减率随测量间隔的变化,其中实线、虚线、点虚线分别代表 Δ= 1,2,5时的情形.由图2可以看出:当测量间隔 τ很小时,出现量子Zeno效应;而当测量间隔 τ足够大时发生量子反Zeno效应.对比实线、虚线、点虚线可以看出,有效衰减率随失谐 Δ的增大而增大,这意味着增大失谐会减小量子系统的生存概率.该结果表明,失谐对生存概率有不利影响.这是因为,非共振条件下,失谐越大,二能级系统与经典驱动场之间的相互作用越弱.也就是说,大失谐条件下,外部经典驱动场对量子态生存概率的保护作用较小.幸运的是,对比图2(a)和图2(b),发现亚欧姆环境中有效衰减率的值总是小于在超欧姆环境中的值.此外,由图2(b)和图2(c)可以看出,增大拉比频率 Ω也可以减小衰减率的值.因此,虽然失谐对生存概率有不利影响,但这种影响可以通过增加经典驱动的强度或选择适当的环境欧姆参数来抑制.

将(13)式代入(3)式,借助于数值计算,展示初态 |ψ〉=|1〉且 Δ=0 ,G=0.01 ,ωc=10 ,Ω=50时有效衰减率 Γ(τ) 随测量间隔 τ变化的函数,其中实线、虚线、点虚线分别代表欧姆参数 s =0.5 ,1.0,2.0时的情形.很显然,在这种情况下发生了多次量子Zeno效应和量子反Zeno效应的转换.也就是说,当测量间隔减小时,生存概率有时会增加,而有时则相反.此外,从图3还可以看出,当测量间隔较短时,超欧姆环境(即 s =2.0)的有效衰减率大于亚欧姆(s =0.5)和欧姆(s =1.0)环境的有效衰减率.然而,在测量间隔相对较长的情况下,超欧姆环境(即 s =2.0)的有效衰减率却最小.这些结果表明,环境的欧姆性对量子系统初态的保持起着重要作用.值得注意的是,比较图3和图1可以发现,对于相同的测量间隔,初态下有效衰减率的值远远小于 |ψ〉=|1〉时的值.
值得注意的是,进一步计算初态为 |ψ〉=|0〉时的情况,得到的数值结果与图3所示的初态为|ψ〉=|1〉时的情况完全一样,也就是说,只要二能级系统初始处于非叠加态(如果是自旋,则为自旋向上 |↑〉或者向下 |↓〉),都会出现图3所示的这些现象.

图3 初态 |ψ〉=|1〉时有效衰减率随测量间隔的变化曲线Fig.3.Behavior of the effective decay rate as a function of the measurement interval for the initial state |ψ〉=|1〉.
5 总 结
考虑了一个受经典场驱动的二能级系统与一个零温玻色子环境相互作用,根据量子系统的有效衰减率随测量间隔的变化,研究量子Zeno效应和量子反Zeno效应,重点讨论经典驱动强度对量子系统生存概率的影响.结果发现,量子系统初始为叠加态情况下,当测量间隔很小时,出现量子Zeno效应;而当测量间隔足够大时发生量子反Zeno效应.但在量子系统初始为非叠加态时,出现了多次量子Zeno效应和量子反Zeno的转换.在相同测量间隔内,初始叠加态时的有效衰减率远远小于初始非叠加态时的衰减率.更为重要的是,当经典驱动足够强时,有效衰减率很小,这表明经典场驱动可以提高量子Zeno和反Zeno效应中量子系统的生存概率.此外,还发现另外一个对量子系统生存概率起重要作用的因素,那就是环境的欧姆性.而二级系统与经典场之间的失谐对生存概率有不利影响,即随着失谐量的增加,生存概率降低.但是,失谐的这种负面影响可以通过增加经典驱动的强度或选择适当的环境欧姆来抑制.
随着实验技术的不断发展,量子Zeno效应和量子反Zeno效应均已被实验所证实[8-12],本项研究也有望在实验中得到实现和验证.首先,二能级量子系统可以用离子内态来实现,用电子搁置的方法实现对离子的测量[12].外部经典驱动场可以控制经典场的强度以及二能级系统与场相互作用的失谐量[32].激光驱动离子方案在实验上很容易实现[33,34].本文讨论的是单个二能级系统,可以用欧姆环境特性可调的自旋玻色子模型实验实现[35,36].本项研究为量子状态的保护实验提供了理论参考.
