激光辐照下红外测温的误差补偿方法研究

2019-12-13苏成志张承双包艳玲阮英波

应用光学 2019年6期

苏成志，晏春，王菲，张承双，包艳玲，阮英波

(1.长春理工大学人工智能研究院，吉林长春 130022；2.长春理工大学机电工程学院，吉林长春130022；3.长春理工大学光电工程学院，吉林长春 130022；4.西安航天复合材料研究所，陕西西安 710000)

引言

碳纤维复合材料具有高强度、低密度以及良好的热力学性能等优点，在现代工业、军事、航空航天等领域有广阔的应用前景[1-3]。将复合材料成型为构件是复合材料应用的关键，尤其是激光原位成型技术以其效率高、不受场地及构件尺寸限制等优点，正在为复合材料的应用带来新的技术变革[4-6]。碳纤维复合材料激光原位成型过程中，为了提高成型质量，应精确控制加热点温度。目前对温度的测量较为常用的测量方式有红外测温[7]和热敏电阻两种方式，采用红外测温仪可实现成型过程非接触在线测温。然而，红外测温易受发射率、环境温度、测量距离、测量角度以及干扰等外界因素的影响[8-9]，难以实现对加热点温度的精确测量,影响成型质量。所以，对红外测温误差补偿是实现对加热点温度精确测量的有效手段，对实现碳纤维复合材料的高质量成型具有重要意义。

针对红外测温误差补偿的问题，Hijazi A等[10]研究了在双波长红外测温中由于发射率的影响出现的测量误差，并利用NGCF进行补偿提高了测温精度；Wang Y H[11]、石东平[12]分别针对环境温度对红外测温的影响，建立了基于环境温度的补偿模型，提高了红外测温仪的测量精度；王超群[13]研究了红外测温中测量距离超出红外测温仪的有效范围时，红外测温仪视场超出目标的红外测温误差修正方法；Wei S[14]等研究了测量角度对红外测温的影响及其误差补偿模型。上述研究中，均是基于发射率、环境温度、测量距离、测量角度等单一变量对红外测温误差补偿进行研究，在一定程度上提高了红外测温仪的测量精度。

本文介绍了激光辐照下加热点处红外测温精度的研究，提出一种测量距离与测量角度的二元线性多变量综合误差温度补偿模型，提高红外测温精度，为碳纤维复合材料的高质量成型提供单元技术支撑。

1 红外测温原理

红外测温仪接收红外辐射的多少会直接影响红外测温的精度，在激光辐照下，除了测量距离、测量角度会对红外测温仪测量结果有影响外，红外测温仪接收到的物体反射的激光也会对测温结果有影响。红外测温原理图如图1所示。

图1 红外测温原理图Fig.1 Schematic diagram for infrared radiation

红外测温仪接收的波长λ的辐射功率Pλ为

Pλ=ARA0d-2[τa(εLλ(T0)+(1-α)Lλ(Tu))+

εaLλ(Ta)]+(k-1)ARA0d-2{τa(ε1Lλ(T1)+

(1-α1)Lλ(Tu)+εaLλ(Ta))}

(1)

(1)式中，AR、A0红外测温器的入射透镜的面积、为红外测温器最小空间张角所对应的目标的可视面积；d为测量距离；T0、Tu、Ta为被测目标体的表面温度、环境温度、大气温度；ε、εa为物体表面的发射率、大气发射率；τa为大气的光谱透射率；α为物体表面的吸收率。

令k=A/A0；A=π(D/2S·d)2，S/D是红外测温仪的距离系数；AARd-2=Km；Pλ/Km=Lλ(Tr)。由(1)式可以得出：

(1-α1)Lλ(Tu))+εaLλ(Ta)}

(2)

根据普朗克辐射定律及斯特藩-玻尔兹曼定律，(2)式可以变为

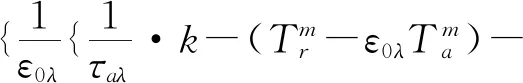
(3)

其中：Tr为测温仪直接测量所得的全视场范围内的温度；m与被测物辐射波长有关的常数。

对于测量距离d在300 mm～350 mm范围变化的短距离测量，大气透过率对测量结果的影响可以忽略。碳纤维复合材料原位成型中，为了保证较好的成型质量，复合材料表面树脂最佳粘结温度为400±10℃(即误差±2.5%)，该温度远高于环境温度，所以环境温度对于测温影响可以忽略。则(3)式可以变为

(4)

根据(4)式，当S/D=150∶1、被测目标直径为2 mm、测量点温度为400℃、测量距离d在300 mm～400 mm范围变化时，测量距离-测量温度理论曲线如图2所示。

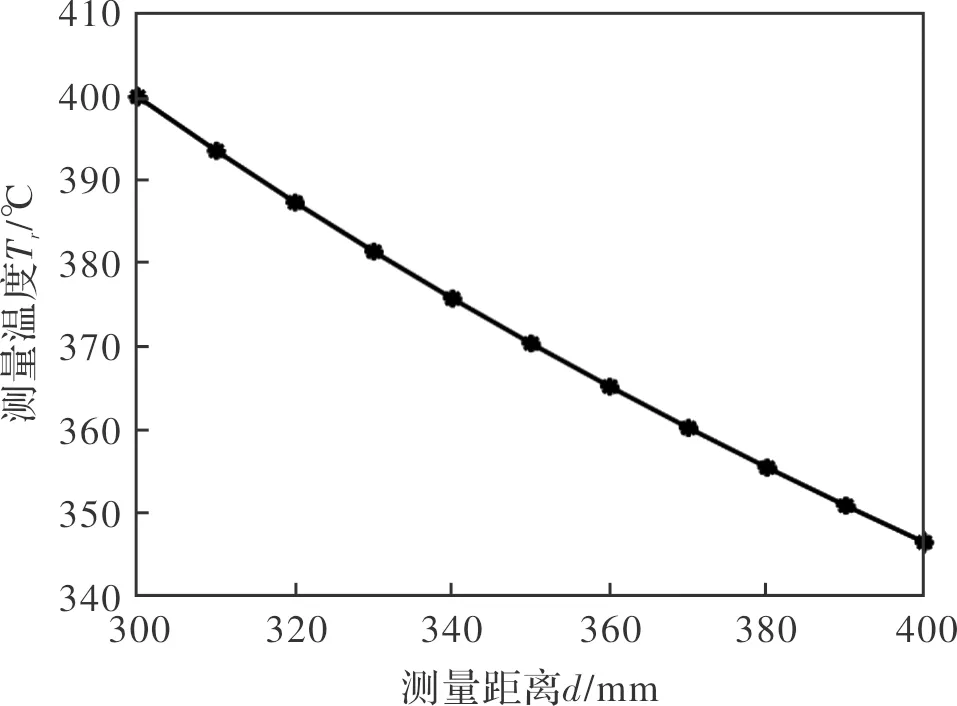
图2 测量距离-测量温度理论曲线Fig.2 Theoretical curve for measuring distancemeasuring temperature

由图2可见，测量距离d对红外测温有直接影响，d在300 mm～400 mm时，随着测量距离的增大，测量温度呈现逐渐减小的趋势，且测量距离与测量温度近似为线性关系，即测量距离越大测量温度越低，测温误差也越大。

如图1所示，在测温过程中，由于条件限制，红外测温仪往往不能安装在最佳位置，导致红外测温仪视场与辐射法线方向形成夹角θ，不能完全吸收红外辐射，从而对测温产生影响。

物体辐射能量时，与理想黑体辐射之间的关系可以表示为

M=ε(T,λ)·Mbb(T,λ)

(5)

其中:M是物体的实际辐射；ε(T,λ)是物体的实际发射率；Mbb(T,λ)是理想黑体辐射定律；结合斯特藩-玻尔兹曼定律，则有：

M=ε(T,λ)·εT4

(6)

假设测量角度对红外测温仪接收到的辐射有一定的影响，则红外辐射与测量角度之间的关系为

M(θ)=m(θ)·ε(T,λ)·εT4

(7)

取ε(T,λ)为常数，红外测温仪接收到的红外辐射，可以用测量温度直观表示出来，则有：

Tr=m(θ)·T0

(8)

其中，一般θ<30°为宜，m(θ)随θ的增大而减小，且0

当激光束投射到物体表面上时，部分被物体吸收，部分被反射，其余则透过物体。被物体反射的激光将被红外测温仪接收，即物体反射的激光会影响红外测温仪测量精度。

2 实验方案

为了研究反射激光、测量距离、测量角度对红外测温的影响，设计了如图3所示的实验方案。

图3 红外测温实验原理图Fig.3 Infrared thermometry experimental schematic diagram

如图3中，α为红外测温仪与二维平移机构竖直方向夹角，θ为红外测温仪与被加热材料测量点法线之间夹角，即测量角度，且θ=90°-α，d为测量距离。在碳纤维复合材料激光辐照时，采用标准热电偶和红外测温仪同步采集加热点温度，并以标准热电偶测量温度作为标准温度。通过角度调节装置、水平位置调节装置、竖直方向调节装置，实现对测量距离d与测量角度θ的调节，完成不同实验条件下加热点温度的红外测量。

实验中激光波长为976 nm，本实验中选择的复合材料对该波长的激光吸收最好，红外测温仪的型号为IR-CD0208A,测温范围200℃～800℃，输出信号是4 mA～20 mA的电流信号，中心光谱为1.6 μm，发射率ε=0.8，距离系数S/D=150∶1，最佳测量距离为300 mm,最小测量直径为2 mm。

3 实验与结果分析

3.1 激光反射对测量温度的影响

在激光辐照加热时，有部分激光被碳纤维复合材料反射进入红外测温仪，对测温造成干扰，从而导致红外测温出现测量值与真实值的极大偏差。为了消除反射激光对测温的干扰，在红外测温仪前端安装了一个滤光片，滤光片透射光谱如图4所示。从图4中可以看出，在500 nm～1 200 nm波段无法通过滤光片。在测量距离d=300 mm、不同温度条件下进行实验，反射激光抑制前后结果如图5所示。

图4 滤光片透射光谱图Fig.4 Transmission spectra of filters

图5 反射激光抑制前后测温与误差 Fig.5 Temperature measurement and error before and after reflection laser suppression

从图5(a)和图5(b)可以看出，在未加滤光片时，由于反射激光进入红外测温仪，导致测量温度远高于标准温度，测量的误差高于300℃，大大降低了测量值的可信度。利用滤光片对反射激光进行抑制后，测量温度与标准温度接近，测量误差为0℃～5℃，此时反射激光对测温的产生的干扰可以忽略。

3.2 单变量对测量温度的影响

3.2.1 测量距离对测量温度的影响

通过在红外测温仪的接收器前置入滤光片抑制反射激光干扰，及测量角度θ为0°时，调节二维平移台竖直方向位置调节装置，对d=300 mm开始,每隔10 mm分别对标准温度T为395℃、400℃、405℃的加热点进行红外温度采集，结果如图6所示。

图6 不同测量距离度不同温度下测温结果与误差Fig.6 Temperature measurement and error at different distances and temperatures

由图6(a)可以看出，d在300 mm～350 mm范围变化时，随着测量距离的增加，所测温度曲线近似线性下降。这是因为随着测量距离增大，红外测温仪的视场超出加热点范围，视场中的背景环境温度对测温产生影响，使得测量温度降低。图6(b)中，测量距离增大时，测量误差呈线性不断增大，最大误差可达到-30%，远远超出测量允许误差ΔT(-2.5%～2.5%)的范围，对成型质量影响很大。可见加热点温度红外测量过程中，距离对测温精度的影响不可忽略。

3.2.2 测量角度对测量温度的影响

在保证距离d=300 mm不变前提下，通过角度调节旋钮调节α，使测量角度θ在0°～30°范围。对标准温度T分别为395℃、400℃、405℃的加热点进行温度采集，结果如图7所示。

由图7(a)可知，在测量距离d=300 mm、θ为0°～30°范围，随着θ的增加，红外测温仪与辐射法向的夹角越大，进入红外测温仪的红外辐射越少，测量温度越低，与标准温度相比呈下降趋势，但是与d(300 mm～350 mm)变化引起测温值的变化相比，测量角度θ(0°～30°)变化引起测温值变化不大。由图7(b)可以看出，θ增大时，测量误差不断增大，最大误差ΔT可达到-3.5%，也超出测温允许误差范围(-2.5%～2.5%),影响成型质量。可见测量角度对红外测温精度也有影响，角度对测温的影响及补偿方式的研究有着实践意义。

图7 不同角度不同温度下测温结果与误差Fig.7 Temperature measurement and error at different angles and temperatures

3.3 测量距离与测量角度正交变化对测温结果的影响

由以上分析可知，测量距离、测量角度对红外测温精度的影响不可忽略。在加热点标准温度为400℃时进行测量距离d与测量角度θ的正交实验，实验结果如图8所示。

由图8(a)可以看出，随着d与测量角度θ的增大，测量温度总体呈线性趋势急剧下降。在同一测量距离d、不同测量角度θ时，温度测量值变化较为缓慢，同一测量角度θ不同测量距离d时，温度测量量值剧烈变化。由图8(b)可以看出，测量距离d与测量角度θ增大时，测量误差不断增大，ΔT最大在-35%左右，误差比测量距离d或测量角度θ单独作用时都要大，远远超出测温允许误差范围(-2.5%～2.5%)。所以建立基于测量距离与测量角度的误差补偿模型，提高红外测温精度，将测温误差降低至成型精度要求范围内是非常有必要的。

图8 400℃角度与距离正交时温度与误差Fig.8 Temperature and error when angle and distance are orthogonal at 400℃

3.4 红外测温多变量补偿研究

温度补偿模型多元线性回归的模型为[15]

Y=β0+β1x1+β2x2+β3x3+ε

(9)

其中：β0、β1、β2、β3是4个待估计的参数；x1、x2、x3是3个可以精确测量或控制的一般变量；ε服从正态分布。在本研究中，x1、x2、x3分别是测量距离、测量角度、测量温度，Y表示经过补偿输出的温度值。在测量距离d和测量角度θ的取值范围内，取不同的测量距离d值与θ值测量的温度值对数据处理进行处理，得到多元线性回归的模型为

Y=-670.5+2.3x1+0.5x2+0.95x3

(10)

为了验证多元回归方程的准确性，进行正逆行程的测量实验，结果如图9所示。

从图9(a)与图9(b)中可以看出，加热点温度为400°，正逆行程测温误差ΔT范围是±1.25%，在允许测温误差范围(-2.5%～2.5%)内。可见测量距离d与测量角度θ共同影响测温精度时，通过补偿模型红外测温仪可以实现加热点温度的较高精度的测量。从图9(c)可以看出补偿模型的回程误差不明显，具有良好的线性度和可逆性，与补偿之前相比测温精度提高64.25%，补偿后的红外测温仪精度可以满足激光辐照下加热点温度的测量要求。