盾构隧道内堆载引起的隧道转动和错台变形计算
2019-12-13齐永洁吴华君
魏 纲, 齐永洁, 吴华君
(1. 安徽理工大学土木建筑学院, 安徽 淮南 232001; 2. 浙江大学城市学院土木工程系, 浙江 杭州 310015; 3. 义乌工商职业技术学院, 浙江 义乌 322000)
0 引言
在上穿既有隧道的盾构施工或者基坑开挖工程中,下部既有隧道因上部土体的卸荷效应会出现上浮变形[1-2]。常见的控制隧道上浮的措施包括盾构掘进参数调整[3-4]、土体注浆加固[5-7]、隧道内压重[8-10]、采用抗浮板等。其中,隧道内压重主要通过在轨道上堆放钢垫块[10]、钢轨[11]、袋装钢渣[12]等方式控制隧道的上浮变形,效果较为明显,但对堆载量及堆载范围要求严格,压载前需进行专门核算[13]。因此,研究盾构隧道内堆载对隧道的变形影响具有现实必要性。
针对隧道内堆载课题,国内外研究者已开展了一些研究,主要的研究方法包括数值模拟[8-11,14-17]、现场实测数据分析[9-12,15,17]、理论解分析[16]。在数值模拟研究方面,张建安等[14]采用Midas/GTS软件建立三维弹塑性模型,对既有地铁隧道内部的最佳压重值进行了研究,通过不同压重值之间的参数分析以及工程类比,确定最佳压重值为50 kPa,但其仅针对单个工程进行了模拟研究,缺乏普遍性,且研究因素未考虑堆载范围变化的影响。在现场实测数据分析方面,廖少明等[15]对夹穿工况下运营隧道的竖向位移进行了实时监测,通过分析实测的上浮趋势线,验证了采用隧道内部压重等控制措施能够对隧道上浮变形起到一定的抑制作用。在理论解分析方面,郭劲睿等[16]采用布辛耐斯克解计算卸荷土体产生的附加应力,将下卧隧道视为无限长梁,根据温克尔地基模型计算隧道的沉降变形,但弹性地基梁模型过于简化,未考虑盾构隧道的管片环连接结构。由以上研究可知,目前关于盾构隧道内部堆载引起的隧道受力和变形的理论解研究还存在不足,有必要对此展开研究。
本文根据魏新江等[18]提出的可综合考虑管片环错台和转动变形效应的协同变形模型,推导计算隧道内堆载对隧道结构产生的附加应力,并结合刘晓强等[19]提出的能量变分法,推导出隧道的沉降及变形计算公式。最后通过Midas数值模拟方法和2组工程案例对本文方法进行了验证,并分析了不同堆载大小、堆载长度、土质条件对隧道变形的影响规律。
1 计算方法
本文基于二阶段分析法,首先计算堆载作用下盾构隧道的附加应力,再通过转动错台协同变形模型计算隧道的沉降及变形。本文假设隧道具有足够的刚度,隧道内部荷载会传递到土体中,在一定范围内隧道会受到土体的反向荷载作用;另外,不考虑压载轨面与隧道拱底之间较小范围内可能发生的应力扩散影响。同时,本文对既有隧道内压重进行单因素分析,研究其对隧道纵向变形的影响规律,假定在隧道压重前既有隧道与周围土体的变形已趋于稳定、浆液均已凝固,后续计算产生的沉降及变形均为隧道内压重直接导致。
1.1 盾构隧道内堆载力学模型
在既有地铁隧道内部道床上进行集中堆载,堆载区域为沿隧道纵向的矩形区域,长度和宽度分别为L和B。盾构隧道内部堆载示意图如图1所示。以矩形堆载区域中心点对应于地面上的垂直投影点作为三维坐标系的坐标原点,沿着矩形堆载区域的长边方向建立x轴,沿着短边方向建立y轴,沿着竖向方向建立z轴。q为单位面积道床上的堆载大小,隧道外径为D,隧道轴线埋深为h。
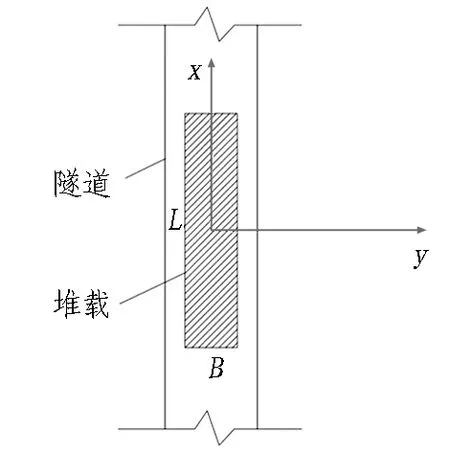
(a) 平面图
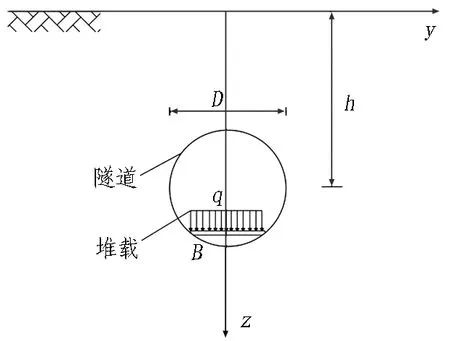
(b) 断面图
Fig.1 Schematic diagram of mechanical model of surcharge in shield tunnel
1.2 隧道受到的附加荷载
由于隧道整体结构具有一定的刚度,作用在隧道内部的均布荷载会通过道床和管片传递到土层中,土层受力的同时会对隧道整体结构有一个反向荷载作用。根据力学模型可知,隧道内部作用荷载为qBL。盾构隧道内堆载引起的土体附加荷载曲线如图2所示。

图2 盾构隧道内堆载引起的土体附加荷载曲线
Fig.2 Soil additional load curve caused by surcharge in shield tunnel
根据文献[7-8]、[20-22]可知,内部堆载引起的隧道沉降曲线一般为正态分布曲线,即
(1)
式中:Smax为隧道沉降最大值;i为从沉降曲线对称中心到曲线拐点的距离。
由温克尔地基模型可知,力与位移成正比,故可以将隧道内部作用荷载引起的土体附加荷载视为正态分布形式,推导求得附加荷载的分布函数为
(2)
式中fmax为同一断面内(x坐标相同)附加荷载的最大值。
在式(1)中,正态分布曲线主要分布区域为(-3i,3i),在(-∞,-3i)及(3i,+∞)2个区间上的函数值几乎为0。由于隧道内部作用荷载的合力与土体附加荷载的合力相等,根据沉降的主要分布区间即可确定荷载的正态分布函数f(x)的主要分布区间(视二者相等)为(-3i,3i)。
将qBL代入式(2)得到
(3)
由式(3)推导可得
(4)
fmax出现在堆载中轴线上(投影在x轴上),则
fmax=qB。
(5)
由式(4)和式(5)整理可得
(6)
将式(5)和式(6)代入式(2)即可得到完整的荷载正态分布函数
(7)
1.3 考虑转动和错台的协同变形模型
本文引入魏新江等[18]提出的考虑转动和错台的管片环协同变形模型,将盾构隧道每环管片简化成弹性地基短梁,环间通过法向弹簧和剪切弹簧连接。该模型认为管片环之间会同时产生相对错台和相对转角变形,两者共同作用导致了隧道的纵向变形。盾构隧道管片环协同变形示意图如图3所示。
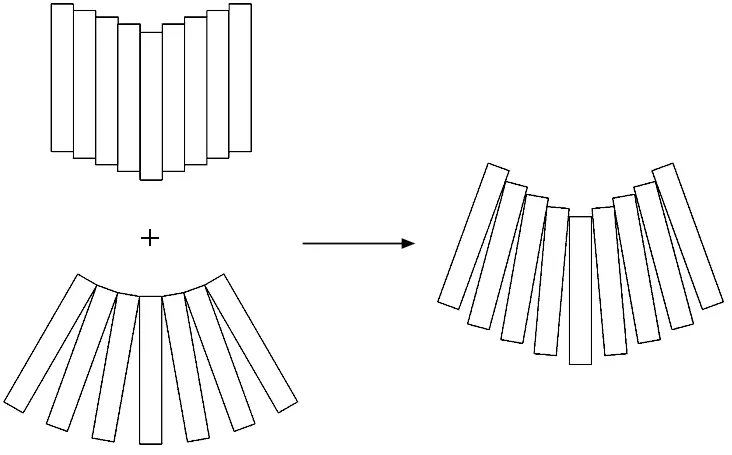
图3 盾构隧道管片环协同变形示意图[18]
Fig.3 Cooperative deformation diagram of shield tunnel segment ring[18]
1.4 盾构隧道总势能
参照魏新江等[18]的研究成果,任取盾构隧道管片的其中1环进行分析,编号为m。刚体转动导致的衬砌环相对位移
(8)
式中:Dt为管片环宽度;θ为管片环间转动角度。
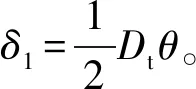
(9)
再求得环间剪切力
(10)
式中: Δω(m+1)为m+1环管片的位移量; Δω(m)为m环管片的位移量;kt为盾构隧道的环间剪切刚度。
环间拉力
Fs=ksθD。
(11)
式中ks为盾构隧道的环间抗拉刚度。
地层抗力
Fk=kDω(x)。
(12)
式中:k为地基基床系数;ω(x)为盾构管片位移量。
设S(x)为土体沉降值,根据位移协调条件有S(x)=ω(x),则所受到的竖向荷载
Fz=f(x)-kDS(x)-kt[Δω(m+1)-Δω(m)]。
(13)
其中,k采用Vesic公式计算,则
(14)
式中:b为地基梁宽度;EI为隧道的等效抗弯强度;μ为土的泊松比;E0为地基土的变形模量。
通过进一步计算可以得到隧道内堆载引起的隧道总势能
Ep=Wp+Wk+Ws。
(15)
式中Wp、Wk、Ws分别为堆载引起的附加荷载做功、管片环克服地层抗力做功、剪切力做功。
1.5 盾构隧道衬砌环的位移函数
能量变分法原理中通过假定合适的位移函数来表示隧道受到洞内集中荷载影响的基本变形形状。
假设盾构隧道的竖向位移函数为
(16)
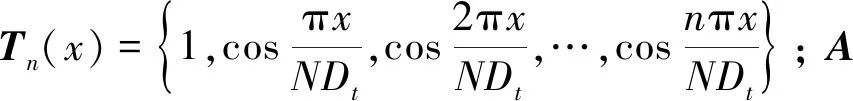
1.6 变分控制方程
基于能量变分法,将总势能Ep对各待定系数取极值,即
(17)
式中ξi为矩阵A中各个元素,ξi=a1,a2,…,an。
对式(17)求解,可以得到盾构隧道竖向位移的控制方程为
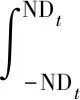
(18)
将式(18)表达为矩阵形式,则
([Kt]+[Ks]){A}T={Pz}T。
(19)
式中: [Kt]为隧道环间刚度矩阵; [Ks]为土体刚度矩阵; {Pz}T表示自由土体位移和盾构隧道衬砌环的相互作用效应。
[Kt]、[Ks]、{Pz}T的计算公式分别为
Tn(mDt)T}·{Tn[(m+1)Dt]-Tn(mDt)}};
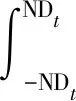
进一步计算可得相对环间错台量,即相邻管片的位移差
Δω=ω[(m+1)Dt]-ω(mDt)。
(20)
相邻盾构管片之间的剪切力
Q={ω[(m+1)Dt]-ω(mDt)}jkt。
(21)
式(20)—(21)利用Matlab进行编程即可计算。
通过上述方法可以求得隧道内堆载引起的纵向变形控制量。实际工程中,上部基坑及隧道的开挖均会造成既有隧道的上浮变形,可通过文献[23]和文献[24]中关于新建隧道上穿和基坑开挖引起下卧隧道隆起变形的计算方法求得具体变形值,再叠加本文方法计算得到的纵向变形控制量,即可求得实际工程中隧道在堆载前后的沉降变化情况。
2 实例及有限元模拟验证分析
由于盾构隧道内压重对既有隧道造成的影响以纵向沉降为主,所以本文选取了隧道内压重的2个工程案例,采用本文方法计算隧道纵向沉降,并与实际数据进行对比,以验证本文方法的可靠性。同时,利用Midas软件进行隧道内堆载的有限元模拟,将得到的隧道沉降曲线进行对比分析。
2.1 实例对比分析
现有成果中缺乏单独分析隧道内堆载引起隧道纵向变形的研究。本文将隧道内堆载对隧道的影响进行单独分析。单纯的隧道内堆载会造成隧道的下沉变形。而本文选用的工程案例为盾构的上穿及夹穿工况,且采用的变形控制措施不仅是隧道内堆载,故在分析过程中需要进行对比计算才能求得单独由隧道内堆载引起的隧道纵向变形值。为了确保计算方法的可靠性,特选取了2个工程案例进行验证。
2.1.1 工程案例1
在上海某盾构隧道上穿地铁工程[8]中,由于盾构掘进造成的卸荷效应使得既有地铁出现上浮变形,施工中采用路面堆载、隧道内堆载等抗浮措施。其中,既有隧道堆载质量为600 kg/m,堆载长度L=25 m。
根据本文的计算方法,首先,根据计算公式(5)求得fmax=5.88 kN;然后,代入公式(7)中可以求得荷载正态分布函数f(x)=5.88exp(-x2/200);最后,通过Matlab软件计算可得由于堆载引起的隧道沉降曲线。
采用本文方法计算得到的工程案例1中隧道沉降曲线如图4所示。由图4可知,隧道纵向沉降最大值为0.117 mm。通过与文献[8]的研究成果进行对比,发现2种方法得到的隧道沉降曲线整体趋势相同。文献[8]得到的隧道顶部下沉最大值为0.146 mm,底部下沉最大值为0.134 mm,与本文方法所得的隧道最大沉降值0.117 mm较为接近,满足精度要求。
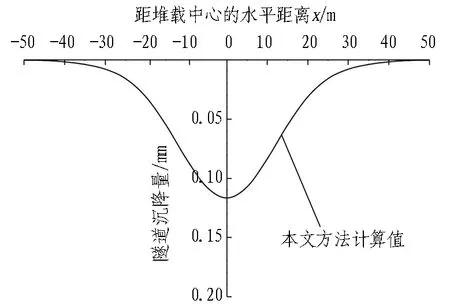
图4 工程案例1中隧道沉降曲线
2.1.2 工程案例2
在上海某夹穿工程中采用了既有隧道和新建隧道分别压重的措施控制上浮,并利用数值模拟的方法对5种压载方案进行了对比分析[9]。此处取工况2和工况3进行对比分析。其中,工况2为对照组,仅在新建隧道内部进行压重;工况3不仅在新建隧道内部进行压重,而且在既有隧道内部进行压载,压载大小为600 kg/m,压载长度L=30 m。则可将工况2和工况3产生的隧道沉降差值视为既有隧道内压重引起的,其差值约为0.25 mm。
根据本文的计算方法,首先根据式(5)可以得到fmax=5.88 kN;然后,代入式(7)中可以求得荷载正态分布函数f(x)=5.88exp(-x2/288)。相关土体参数参考王有成等[11]关于同一工程的研究结果。
通过Matlab计算可得到由堆载引起的工程案例2中隧道沉降曲线如图5所示。隧道最大沉降量为0.162 mm,与采用文献[9]中的方法得到的结果虽然存在一定误差,但在允许范围内。

图5 工程案例2中隧道沉降曲线
2.2 有限元模拟对比分析
本文利用Midas进行有限元模拟验证。采用的工程参数:L=30 m,B=3 m,q=9.8 kPa; 泊松比μ=0.35,土体重度γ=18.19 kN/m3,黏聚力c=16.66 kPa,土体内摩擦角φ=20.78°,土体压缩模量Es=7.35 MPa,土体弹性模量取25 MPa;EI=1.1×108kN·m2,kt=7.45×105kN/m,ks=1.94×106kN/m,j=0.2,b=0.3 m;D=6.2 m,h=12 m,Dt=1.2 m,N=100。
在数值模拟中,隧道模型采用平面板单元,土体采用实体单元,满足摩尔-库仑理论。计算模型长200 m,宽70 m,高40 m。模型网格划分如图6所示。

图6 模型网格划分
盾构隧道纵向沉降曲线数值模拟位移云图如图7所示。在相同参数条件下,将数值模拟计算所得的沉降曲线与本文计算方法得到的沉降曲线进行对比,结果如图8所示。由图8可知,2种方法得到的沉降曲线均为正态分布曲线,曲线总体变化趋势相同。其中,有限元模拟得到的隧道最大沉降值为0.586 mm,本文方法计算得到的隧道最大沉降值为0.614 mm,差值仅为0.028 mm,满足精确度要求。
2.3 隧道上穿案例的综合分析
在上海某盾构上穿既有隧道工程[23]中,既有隧道受到上部开挖的影响出现上浮变形。其中,既有隧道轴线埋深为19.235 m,新建隧道轴线埋深为11.685 m,隧道直径均为6.2 m。盾构掘进过程中的其他相关参数可参见文献[23]。通过文献[23]中的方法计算既有隧道受到上部新建盾构隧道开挖而引起的纵向隆起量,堆载前后隧道的隆起量如图9所示。同时,为了抑制既有隧道的上浮变形,拟采用隧道内堆载的措施进行控制。堆载方案中选择的压载大小为600 kg/m,压载长度L=30 m。
根据本文的计算方法可以求得隧道内堆载引起的隆起控制值,在隧道隆起值的基础上叠加该部分隧道隆起控制值即可得到最终的隧道纵向变形值。由图9可知,堆载前隧道的最大隆起量出现在隧道中轴线上,大小为1.63 mm,堆载后纵向隆起得到一定控制,中轴线处的隆起量减小至1.47 mm,减小的这部分隆起量即为隧道内堆载引起的沉降控制量。
图7 盾构隧道纵向沉降曲线数值模拟位移云图 (单位: mm)
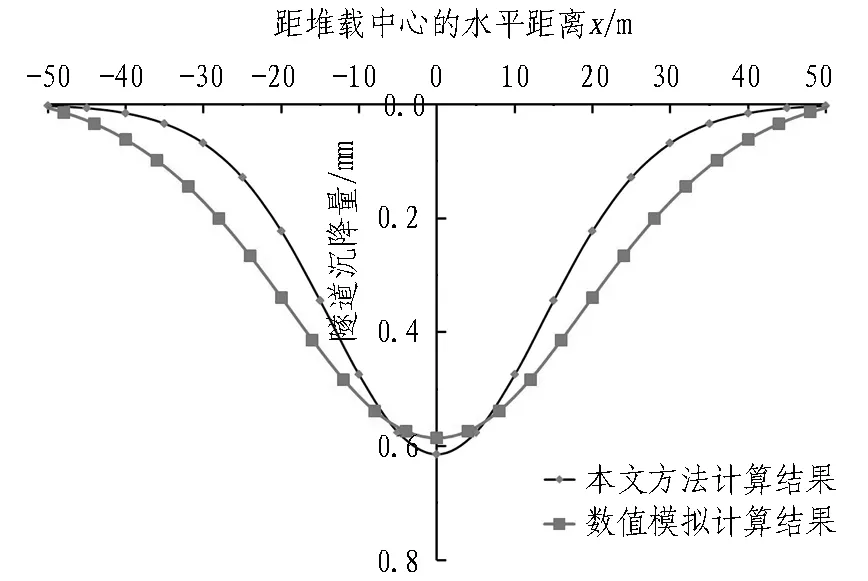
图8 隧道沉降计算结果和数值模拟结果对比
Fig.8 Comparison between calculated results and numerical simulation results of tunnel settlement
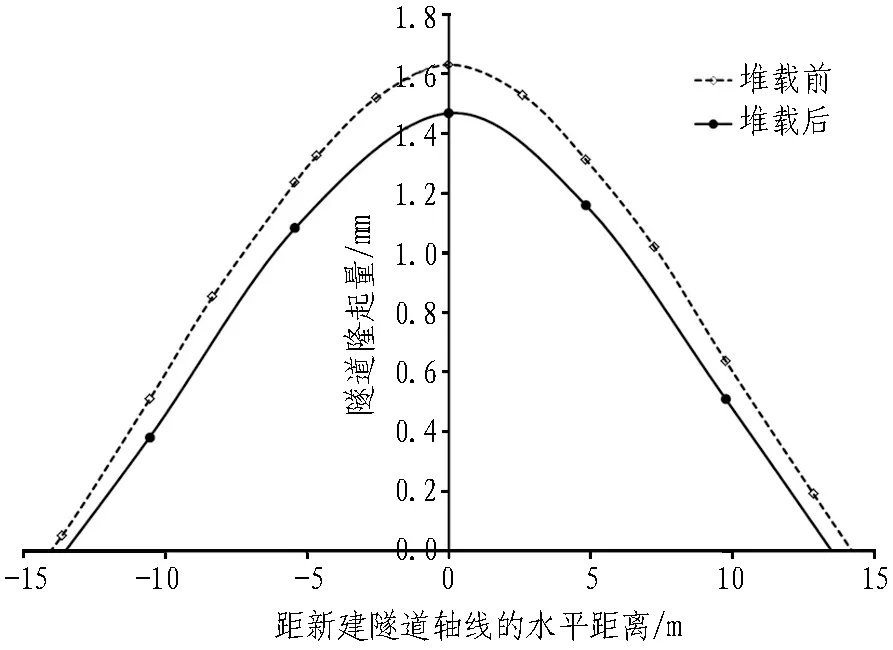
图9 堆载前后隧道的隆起量
Fig.9 Comparison between tunnel uplift values before and after loading
3 隧道变形影响因素分析
数值模型涉及的参数见2.2节。通过计算分析不同堆载大小、不同堆载长度以及不同土质条件对隧道变形量的影响规律。
3.1 堆载大小对隧道变形的影响分析
保持其他参数不变,以堆载大小q为控制变量,分别在q=4.9 kPa、9.8 kPa、14.7 kPa和19.6 kPa 4种工况下计算隧道所受附加荷载、沉降量、环间剪切力、错台量和转角角度,分析q值改变对隧道变形的影响规律。
不同堆载情况下隧道受到的附加荷载如图10所示。随着q增大,附加荷载不同程度地增大,最大值出现在堆载中心,荷载影响范围无明显变化。
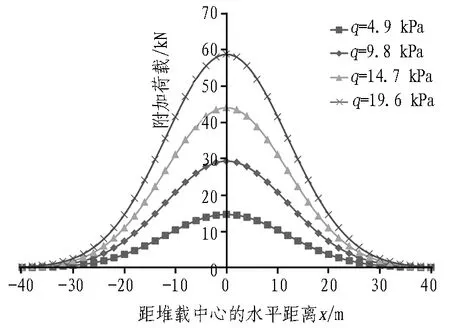
图10 不同堆载情况下隧道受到的附加荷载
不同堆载情况下隧道的沉降量如图11所示。随着q增大,隧道沉降相应增加,最大沉降量出现在堆载中心,依次为0.31 mm、0.61 mm、0.92 mm和1.23 mm,近似呈线性增加。隧道沉降量由所受的纵向附加应力直接决定,故两者变化规律相同,均呈正态分布。采用本文方法计算得到的隧道沉降曲线特征与王有成等[11]对既有隧道进行压钢轨处理后获得的隧道沉降曲线特征相似。另外,戴仕敏[10]关于隧道内加载对既有隧道变形控制的研究也证明了随着加载量的增加隧道的隆起控制越好,且近似呈线性相关,这与本文结论相似。
地铁隧道对于变形控制的要求很高,而管片环处为结构薄弱环节[25],管片环之间的错台量和转角变形对隧道的运营安全影响巨大。当变形超出安全限值时,极易导致隧道出现漏水现象,因此,对环间错台量和转角进行研究十分必要。不同堆载情况下隧道的环间错台量和环间转角分别如图12和13所示。由图12和13可知: 1)环间错台量和转角的变化规律基本一致,随着q的增加,两者均不同程度地增大; 2)靠近堆载中心的位置,环间错台量和环间转角均接近于0,而在堆载中心两侧迅速增大,该变形规律与魏新江等[18]的研究成果相似。3)当q分别为4.9、9.8、14.7、19.6 kPa时,相邻管片相对错台量的最大值分别为0.052、0.104、0.156、0.208 mm,最大环间转角分别为0.011°、0.022°、0.032°、0.043°,最大错台量和最大环间转角均出现在距离堆载中心两侧10~15 m处。
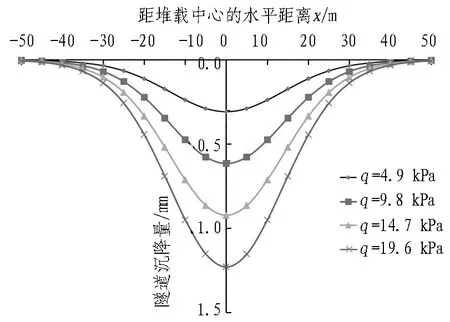
图11 不同堆载情况下隧道的沉降量
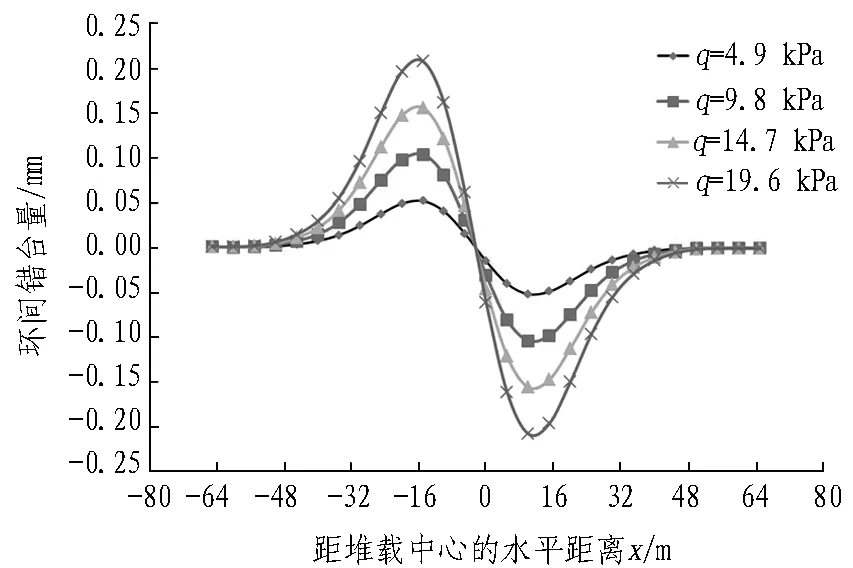
图12 不同堆载情况下隧道的环间错台量
Fig.12 Comparison of dislocation among shield tunnel segment rings under different surcharge
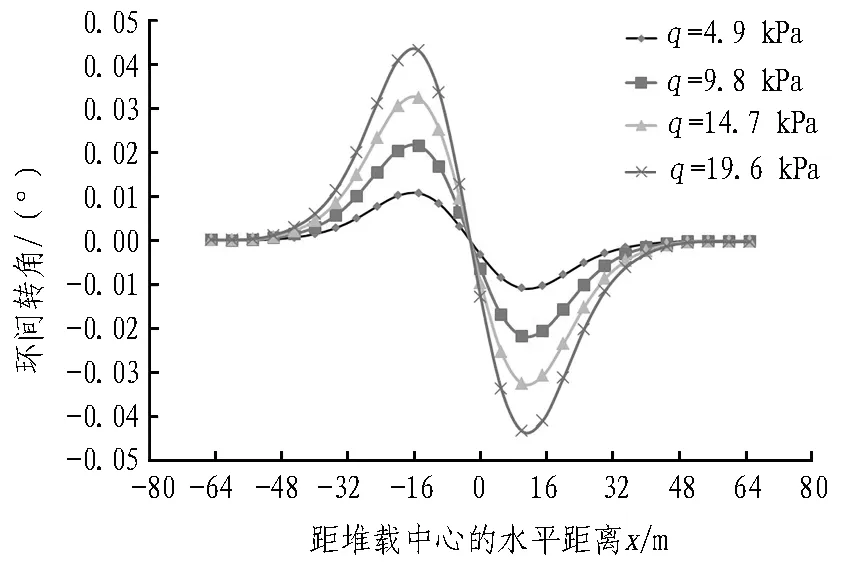
图13 不同堆载情况下隧道的环间转角
Fig.13 Comparison of rotation angle among shield tunnel segment rings under different surcharge
不同堆载情况下隧道的环间剪切力如图14所示。由图14可知,随着q值的增加,环间剪切力不同程度地增大,其最大值依次为38.68、77.36、116.04、154.72 kN,均出现在错台量最大的位置。
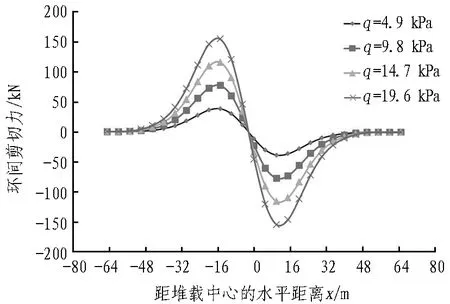
图14 不同堆载情况下隧道的环间剪切力
Fig.14 Comparison of shearing force among shield tunnel segment rings under different surcharge
3.2 不同堆载长度对隧道沉降的影响分析
保持其他参数不变,分别取L为10、20、30、40 m。为了提高Matlab的计算精度,随着L值的增大,选取的N值也相应增大,依次为50、75、100、125。
不同堆载长度下隧道沉降量如图15所示。堆载长度的增大增加了隧道的沉降量,但增加的速度明显减小。沉降最大值出现在堆载中心位置,从小到大依次为0.385、0.542、0.614、0.653 mm。
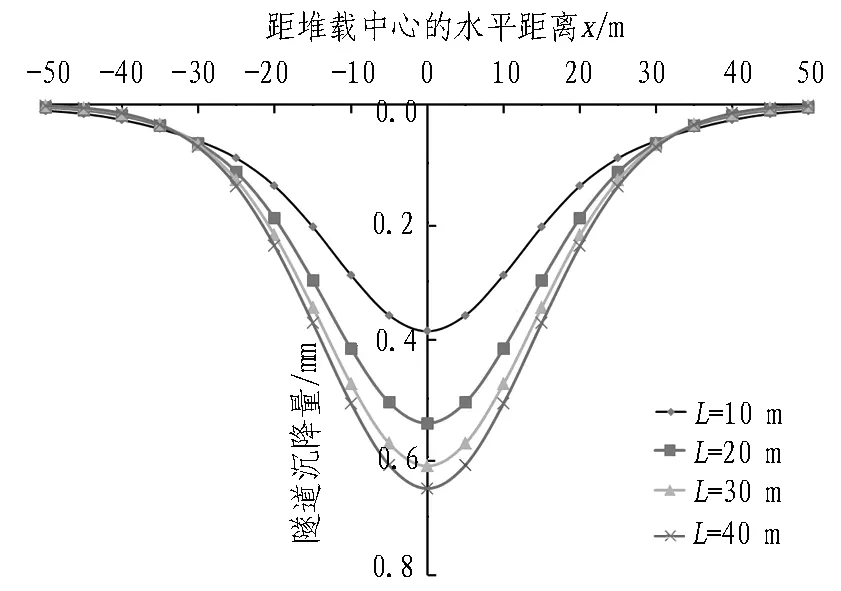
图15 不同堆载长度下隧道沉降量
Fig.15 Comparison of tunnel settlement under different surcharge lengths
3.3 不同土质条件对隧道沉降的影响分析
以2.2节土质作为土质1,另取土质2、3、4进行对比分析。土质2参数:μ=0.42,γ=17.4 kN/m3,c=14 kPa,φ=18°,Es=4 MPa。土质3参数:μ=0.37,γ=18.8 kN/m3,c=15.9 kPa,φ=22°,Es=7.5 MPa。土质4参数:μ=0.4,γ=17.6 kN/m3,c=14.5 kPa,φ=19.2°,Es=6 MPa。其余相关参数均保持不变。
不同土质条件下的隧道沉降量如图16所示。不同土质条件下隧道沉降变化规律相似,沉降最大值均发生在堆载中心位置,在土质1、2、3、4条件下依次为0.614、1.536、0.651、0.935 mm。在相对较好的土质1中,由堆载引起的隧道沉降量及沉降范围均要比其他土质中的小,该结果与房明等[22]的研究结果相似。

图16 不同土质条件下的隧道沉降量
Fig.16 Comparison of tunnel settlement under different soil properties
4 结论与讨论
1)本文计算方法综合考虑了盾构管片环间错台和转动变形,计算结果通过2个典型案例与数值模拟结果进行了可靠性验证,能较好地计算因盾构隧道内部堆载引起的隧道附加应力、沉降量、环间剪切力、环间错台和环间转角。
2)盾构隧道内部集中堆载引起的隧道附加荷载及沉降量沿着隧道纵向呈正态分布,堆载中心的附加荷载及沉降量最大,且与堆载大小近似成正比。隧道环间错台量、环间转角及环间剪切力最大值均出现在堆载中心两侧,在堆载中心处近似为0。
3)堆载长度L依次取10、20、30、40 m时,隧道沉降量相应增大,其中,堆载中心最大沉降量分别为0.385、0.542、0.614、0.653 mm,说明沉降量的增大速度逐渐减缓;堆载参数相同情况下,在土质较好的土层中,由堆载引起的隧道沉降量及沉降范围均较小。
本文计算做了一定简化,假设隧道所受附加荷载与隧道沉降均呈正态分布,未考虑压载轨面与隧道拱底之间的应力扩散影响以及隧道上部结构的开挖卸荷效应,导致计算结果存在一定的误差。后续研究中可以结合实际工况或通过调整相关土体回弹参数来考虑开挖卸荷与洞内堆载的综合作用。另外,实际工程中常将隧道内堆载和土体注浆等控制隧道纵向变形措施同时使用,但为了更清晰地研究隧道内堆载对隧道沉降的影响规律,仅将其作为单因素进行了分析。
