露天矿山开挖边坡爆破振动损伤规律及稳定性分析

陈 涛，黄浩轩，王 珍

(1.黄河科技学院 建筑工程学院，河南 郑州 450000；2.中国煤炭科工集团 沈阳煤炭设计院，辽宁 沈阳 110000)

露天矿山开采过程中，由于频繁受到爆破振动作用，边坡破坏机制及稳定性分析极为复杂，对露天矿山安全生产造成严重威胁[1，2]。边坡爆破振动损伤规律及稳定性分析的研究工作可追溯至20世纪60年代初期，经过几代学者不懈努力取得了诸多代表性成果[3-6]。

边坡爆破振动损伤规律及稳定性分析是一个复杂的、涉及多个相关学科的地质力学问题，国内外众多学者从不同角度探究该问题的解法，取得了可喜的成果。但由于开挖过程中爆破振动作用是一个反复、持续的过程，对于多次爆破振动作用下边坡岩体累积损伤规律的研究基本没有涉及，而露天矿山滑坡演化恰恰存在这种时间效应。针对该问题，本文综合运用工程地质调查、现场试验与测试、理论分析与数学计算等方法，建立边坡爆破累计损伤计算模型，确定滑坡发生的时间及破坏区域，并通过FLAC3D数值模拟软件验证计算结果，达到边坡潜在危险提前预警与防治的目的。

1 边坡损伤模型的建立介绍

1.1 爆破荷载的量化

选取典型露天矿山为工程背景，本矿山开挖边坡爆破过程中，台阶高度h=12m，每次爆破孔数为50个，采用矩形布孔方式，共设置炮孔排数为5排，每排炮孔个数为10个。炮孔孔距a=4m，行距b=3m，炮孔孔深h′=12m，孔底无超深。爆破炸药类型选取为乳化炸药，单孔装药量q=50kg，总装药量Q=2.5t，装药方式为分段装药，起爆方式为毫秒微差起爆。

爆破荷载对边坡的损伤作用是力、能量以及形变三者间相互转移转化的复杂过程，量化爆破荷载对边坡的损伤规律，建立二者间的函数关系式是该领域的研究重点[7，8]。本文应用声波测试仪对边坡爆破振动损伤程度进行测定。测定过程中，选取水作用耦合剂以减少声波与空气接触产生的误差。

在爆破振动作用下，开挖边坡岩体将产生振动裂缝，该振动裂缝迅速被空气充满。众所周知，声波在空气中的传播速度vk近似为340m/s，远小于声波在岩体中的传播速度，因此可通过岩体声波速度降低率近似描述边坡岩体损伤程度，边坡损伤程度η可表示为：

η=(v0-vt)/(v0-vk)

(1)

式中，v0为该开挖边坡岩体的初始声波速度，m/s；vt为该开挖边坡经爆破作用后岩体的声波速度，m/s。应用式(1)可将爆破荷载对边坡的损伤程度进行合理量化。

1.2 边坡损伤分析

根据Morris经验公式，当爆破总药量Q为定值时，边坡损伤程度是爆心距的单值函数，且二者之间呈现近似的反比例关系。为确定二者之间的函数关系式，进行一次爆破试验并选取爆破上部台阶四个不同位置作为测试点进行声波测试。根据本矿山台阶分布规律，爆区中心与测试点的垂直距离(最小距离)为70m，因此选取的爆心距最小值为70m。四个测试点爆心距分别选取为70m，80m，90m，100m，其平面布置如图1所示，边坡损伤程度测试结果见表1。

为确定Morris经验式[9]中边坡损伤程度与爆心距二者间的反比例系数，本文对爆心距取得不同值时损伤程度与爆心距关系进行最小二成拟合，拟合结果如图2所示。

图1 边坡损伤试验平面布置图

表1 边坡损伤程度测试结果

图2 边坡损伤程度拟合结果

曲线拟合结果表明，边坡岩体损伤程度与爆心距的反比例关系是显而易见的，拟合关系式为η=165/D。相关分析结果R2=0.982，相关性能良好，可做为边坡损伤程度的计算方式。

1.3 累积损伤分析

由于开挖边坡频繁受到爆破振动影响，因此应对连续爆破振动作用下开挖边坡损伤规律及稳定性进行分析研究。为确定连续爆破振动作用下边坡岩体损伤规律，共进行四次爆破试验，选取第一次爆区中心上部台阶垂足作为测试点，根据前文分析可知第一次爆破爆心距为70m。根据本矿山爆破参数可得爆破区长度为40m，据此根据勾股定理可得第二、三、四次爆破爆心距分别为81m、106m和139m。其平面布置如图3所示，同时边坡累积损伤程度测试结果见表2。

图3 边坡累积损伤试验平面布置图

表2 累积损伤程度测试结果

由振动在岩体中的传播性质可知，爆破振动对开挖边坡累积损伤程度随爆破作用次数呈现指数衰减的规律。由此可得第n次爆破对该开挖边坡损伤程度的表达式为：

ηn=kn-1×165/D

(2)

式中，k为爆破振动对开挖边坡岩体损伤程度的衰减指数。根据表2中累积损伤程度测试结果对衰减指数k进行最小二成拟合，拟合结果如图4所示。

图4 累积损伤程度拟合结果

曲线拟合结果表明，该开挖边坡岩体累积损伤程度与爆破作用次数呈现明显的指数衰减规律，拟合关系式为ηn=0.95n-1×165/D。相关分析结果R2=0.991，相关性能良好，可作为边坡累加损伤程度的计算公式。

2 边坡稳定性分析

爆破振动作用下边坡稳定性分析应重点考虑边坡的时空效应，即应准确确定边坡破坏时间及边坡最危险区域。该矿山开挖边坡爆破过程中，爆破区长度l=40m，爆破区中心距离上部台阶垂直距离d=70m，假定爆破作用次数为x，其中第m次爆破区中心距离测试位置距离最小，即dm=70m。根据空间距离计算方法，可确定爆心距的计算公式可表示为：

(3)

根据前文中爆破作用下开挖边坡损伤累积损伤程度计算公式，可确定各次爆破对该开挖边坡损伤程度可表示为：

(4)

根据爆破振动作用下边坡工程经验，开挖边坡累积损伤程度大于10%将发生剪切破坏，因此边坡破坏时x应满足：

(5)

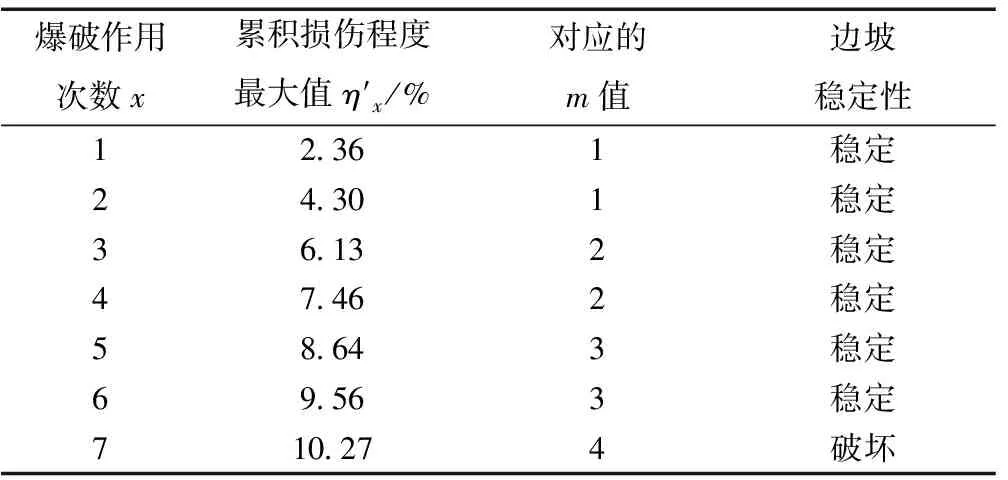
表3 边坡稳定性计算结果

累积损伤计算结果表明，当连续爆破次数达到7次时，该开挖边坡累积损伤程度达到10.27%，此时将发生剪切破坏，对应m=4，即最危险区域位于距离爆破起始位置120～160m处上部台阶。

3 数值模拟分析

为验证上文中计算结果的准确性，采用FLAC3D数值模拟软件对爆破振动作用下边坡累积损伤程度进行模拟。边坡地质模型选取模型尺寸X方向为40m，Y方向为10m，Z方向为18m。根据前文计算结果，共进行7次爆破模拟，并分别建立7个边坡地质模型，各模型分别位于爆破区中心位置处。每次爆破作用后最大剪切应变增量如图5所示，括号内表示最大剪切应变所对应的模型。

数值模拟结果表明，该开挖边坡由于受到爆破荷载作用产生局部剪切变形，随着爆破作用次数增加，剪切变形向坡顶方向逐步扩展，最终形成连续的贯通滑面，边坡岩体将沿该滑面发生剪切破坏。当爆破作用次数达到7次时，该开挖边坡岩体内部滑面贯通，此时边坡发生破坏，此时最大剪切应变对应的为模型4，即最危险区域距离爆破起始位置120～160m。数值模拟结果与前文中计算结果完全一致，充分验证了本文所提方法的准确性。

4 结 论

1)通过现场试验与理论分析相结合手段，建立了边坡爆破振动损伤计算模型，并通过数学计算的方式实现了边坡爆破振动损伤规律研究及稳定性分析的目标。

2)应用 FLAC3D数值模拟软件建立了边坡地质模型，并对爆破振动施加过程进行模拟运算，最终通过剪切应变增量云图实现稳定性分析的目的。

3)计算结果与模拟结果均表明本矿山开挖边坡在连续进行7次爆破作用后上部台阶将发生破坏，最危险区域距离爆破起始位置120～160m处，充分验证了本文提出的计算方法的准确性。