小学数学纸笔测试试题改进探微
2019-12-12马建瑛
马建瑛
(龙岩市永定区教师进修学校,福建 龙岩 364100)
学业质量评价具有导向、诊断、反馈等功能,通过评价改革引领教学行为改进是落实数学核心素养的有效路径之一。目前,纸笔测试作为小学数学学业质量的主要评价方式,因其操作简便、可信度高等优点,被广泛应用于教师的日常教学诊断和区域教学质量监测中。进行纸笔测试至关重要的一环是试题命制,试题作为测量工具,其质量的高低直接关系到诊断与评价的结果是否科学、准确。应改进试题命制,以更科学、准确地评价教学,进而引领教学行为改进,让数学学科核心素养培育目标落地。
一、突出本质,深度理解应用
数学基础知识和基本技能是学生形成数学素养的基石。传统的试题偏重简单描述与再现记忆,因此,教师在教学中往往注重记忆概念条文,或通过反复操练形成技能。例如“分数”这一小学数学核心基础知识的考查,常见以下判断题:
2.假分数一定大于1。()
以上试题虽然能考查学生对分数概念及分类等基础知识的掌握,但这种掌握仍停留在描述与记忆的浅层学习中。《义务教育数学课程标准(2011年版)》的评价建议指出,“对基础知识和基本技能的考查,要注重考查学生对其中所蕴含的数学本质的理解,考查学生能否在具体情境中合理应用。”这为试题命制明确了方向——淡化记忆,注重理解,突出本质。基于课标的这一理念,可把上述两题改编如下:
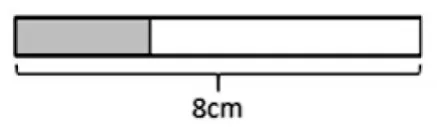
1.图中阴影部分占整个长方形的()分之()。[1]
2.如下图,a、b、c、d是东东在线上找到的四个分数,其中假分数有( )。

A.a B.a和b C.d D.c和d
题1整个长方形长8厘米,学生只需量出阴影部分长3厘米,将测量技能与分数概念理解结合起来,就不难得出准确答案。题2也是采用数形结合的方式来辨别不同类型分数在数轴上的不同位置。两题都不需死记硬背概念条文,而是指向学生对分数内涵的本质理解,考查学生在具体情境中的合理应用。
二、凸显过程,反馈教学实效
学生数学素养的提升离不开扎实有效的数学学习过程,但教师在教学中往往比较注重落实知识技能目标,淡化过程性目标。因此,命制一些指向考察知识形成过程的试题,才能引发教师反思,重新定位教学。例如:
该试题源于教材,教师、学生都非常熟悉,但实际检测得分率却不高。究其原因,以往对计算能力的考查只要能根据运算法则进行正确计算即可,教师在教学中过度强调结果(法则)的认识与运用,却淡化了对运算法则推导过程的探究。实际上,对为什么“除以一个不为0的数等于乘这个数的倒数”的研究,学生可以运用不同的策略,通过已有的通分、商不变规律、分数与除法的关系或分数除以整数的计算等知识经验总结出一个数除以分数的算法。这一过程蕴含着丰富的数学素养培育资源,学生可以从中感悟基本思想,积累逻辑推理和数学论证的活动经验,发展数学思考力。这样指向过程的试题,引导教师重视运算法则推导、归纳过程,通过夯实学习过程发展学生的数学素养。
三、关注表达,体现个性思维
英国数学学习心理学家斯根普指出,学生对知识的理解分为“工具性理解”和“关系性理解”,任伟芳、张奠宙等学者在此基础上提出数学理解的三个层次:“工具性理解”“关系性理解”和“创新性理解”。[3]传统纸笔试题的作答往往是封闭式的,只有一个“标准答案”,无法体现学生对学习内容不同的理解水平及思维层次。针对这一弊端,在纸笔测试时可改变作答方式,鼓励学生用数学语言清晰、有条理地表达自己的想法,体现个性化思维,促进学生思维品质的提升。例如:
24∶()=()∶2,括号里可以填哪些数,你是怎么想的?
本题在考查比例的基本性质时,将传统的封闭式填空改成有向开放式作答,通过学生对思考过程的不同表达,体现对“比例”不同层次的理解掌握水平。该题的回答大致可分为四种水平。水平1:运用比例的基本性质找出一组数,如24×2=6×8,得出24∶(6)=(8)∶2。水平2:运用比例基本性质写出其他答案,如 24∶(6)=(8)∶2,24∶(12)=(4)∶2,24∶(8)=(6)∶2等。水平3:能运用比例的基本性质有序地列举出多种答案,得出能填的数包括1和48,2和24,3和16,4和12,6和8。水平4:思考更加全面,除整数外还能枚举出分数、小数的例子,或能创造性地运用图文、列表等方式表达想法。
其中水平1、2为“工具性理解”,水平3为“关系性理解”水平,而水平4则体现了“创新性理解”,透过学生不同的作答可对其理解水平和思维层次进行诊断,进而可以指导教师改进教学。
四、综合设计,培养应用意识
“数学核心素养是数学学习者在学习数学或学习数学某一领域时应达成的综合性能力。”[4]数学素养之间有较高的相关性,设计综合性、开放性的数学任务是培养和测量数学素养的有效途径。因此,综合性应用型的试题成为纸笔测试中的一个新趋向。例如:
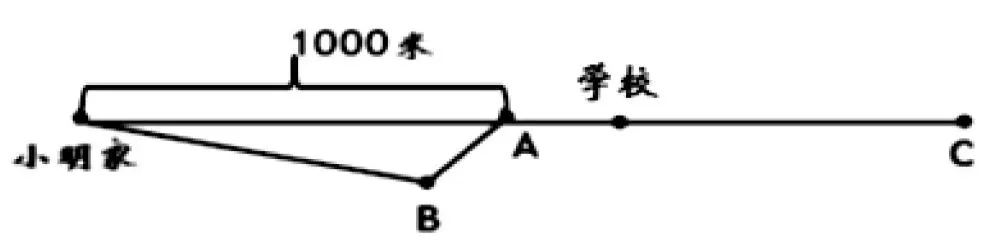
1.小明从学校回家,每分钟走75米,请用△标出小明走了10分钟后的位置并写出理由。
2.小玲家距离学校300米,距离小明家800米,A、B、C三点哪个是小玲家的位置?请说明理由。
此题以学生熟悉的家校路线图为情境,综合考查了路程速度时间的数量关系、三角形的三边关系、整数乘法运算等内容,其中还隐含数感、空间观念的考查。试题既不是生活的原形,也不完全是数学的骨架,信息量较多。学生在解答时要读取、整理信息,并综合运用多个领域知识进行积极的联想和思考,从而解决问题。设计这样的综合性试题,旨在引导教师对教学内容进行整体考虑和有机整合,帮助学生学会沟通知识间的联系,建构起清晰的认知体系,并能在具体情境中整体地考虑问题、解决问题,培养应用意识。
总之,纸笔测试试题改进应始终围绕学科核心素养形成这一目标,突出数学本质、凸显学习过程,提供表达个性思维的空间,通过综合性的问题发展应用意识,发挥测试的导向、诊断、反馈功能,最终达到“教、学、评”的一致。
