基于特征选择的煤层瓦斯含量影响因素分析

朱加锋，单 耀，李红涛

(1.潞安矿业集团公司 通风处,山西 长治 046204; 2.华北科技学院，河北 三河 065201)

煤层瓦斯含量是指单位质量的煤中含有瓦斯气体体积的量。在煤矿开采的过程中，煤中的瓦斯涌出进入巷道，造成巷道瓦斯浓度升高，给安全生产带来隐患，同时造成环境污染。因此，控制井下巷道的瓦斯浓度是煤矿生产的重要工作。另一方面，高浓度的瓦斯本身就是一种能源，可以用来发电、供暖或居民燃气使用。鉴于此，煤矿在井下进行瓦斯预抽采，降低工作面瓦斯浓度的同时，提高了资源的利用率。要想高效地对瓦斯进行抽采，对煤层瓦斯的基本理化参数的分析是一项重要的工作，很多研究者建立了含煤地层瓦斯含量的预测方法，通过不同的手段预测目标煤层的瓦斯含量，为准确高效地抽采瓦斯，同时有效管理通风系统提供技术支持。

煤中瓦斯含量的预测，主要有地质分析，地球物理探测，地球化学与数据分析的方法。基于地质条件的瓦斯含量预测及瓦斯突出的预测，是从含煤地层所处的地质构造变化入手，分析导致瓦斯聚集、逸散的诱因，对地质单元进行划分[1-5]。地球物理方法的原理是利用煤层反射的地震波，建立地震属性与瓦斯含量之间的关系，达到预测瓦斯含量的目的[6-7]。数据分析的方法常基于地质与地球化学的数据建立模型，从建模方法的角度，近些年的文献中主要使用了以下几种方法：单变量线性回归和多元线性回归[8-17]，支持向量机[18-20]，神经网络[21-26]等。

瓦斯含量预测模型的建立，不可避免地涉及到影响因素的确定，或者说变量筛选的问题。参量的选择，对于构建一个合适的模型至关重要。虽然瓦斯的含量与多种因素有关，但影响程度不同。一方面，过少的变量将导致模型的低准确率，或者错误。另一方面，过多的参量，也并不一定会增加模型的准确度，同时还容易导致过拟合的问题。变量的筛选一般通过两种手段来实现，一是基于采矿、地质专业知识的判断以及工程实践经验，二是多维数据的统计分析。在前人的研究中，多使用的是第一种方法。研究者通过地质因素的分析，一般选取煤层埋深，煤的纯厚度，煤的挥发分，围岩条件，断层及组合形态作为模型的自变量指标。在实际问题的分析中，需要将两种方法结合起来使用，才能达到较好的效果。

从数据挖掘的角度来看，选择对煤层瓦斯含量影响程度较大的变量需要在建立合适的模型之前，需要清洗数据，包括数据错误值、异常值、缺失值的处理，数据的规范化与标准化，变量的筛选等，称为特征工程。特征工程包含数据预处理、特征构建、特征抽取与特征选择等几个步骤，主要的方式可以分为过滤法、包装法与集成法，以及基于专业的分析等几类[27]。

包装法以多元回归分析为基础，通过逐步回归的方式找到模型最适合的变量。如郑飞等[12]通过逐步回归从原数据中选择了底板标高、主断层距离、砂泥比与煤层倾角四个变量进行建模。多元线性回归常能获得较好的效果，但自变量之间可能会出现相关性，影响回归方程的稳定性，即多重共线性的问题。Lasso回归是多元回归的一种，通过增加正则项，虽在一定程度上增加了模型预测的误差，却能够大幅度降低多重共线性的影响，增强模型的稳定性。在建模过程中，通过改变正则项的比重λ值，相对不重要变量的系数可以收缩到零，从而达到变量筛选的目的。

集成法的思想是从原数据抽取一部分建立一个模型，通过大量的抽取与建模，然后对这些模型进行统计，对自变量的重要性进行排序，达到变量筛选的目的。随机森林是一种常用的集成算法建模工具，通过多无偏弱分类器-决策树的投票来进行分类。通过从原数据中抽取部分数据建立决策树模型，对森林中使用给定变量进行分类或回归的所有树进行计算，然后计算精度损失的平均值和标准差。此外，重要的特征选择的方法还有提升法(Boost)等。在使用Boost建模时，通过迭代的建模手段，后一次建模时对前一个模型的错误值增大其权重，不断提高模型预测的准确度。

本文研究的目的是分析不同的因素对瓦斯预测的重要性。首先，建立具有较好的准确性模型，控制过拟合的问题，增强泛化能力；其二，通过变量的筛选，获得对煤层瓦斯影响程度较大的地质、工程因素，有助于技术人员深入理解瓦斯含量的影响因素。

1 研究方法

相比较来说，基于随机森林，Lasso和提升法的特征选择的效果和稳定性更好。同时，提升法需要更多的数据，鉴于目前可获得数据有限，提升法并未获得满意的结果，因此本文基于随机森林与Lasso回归的分析过程与结果进行讨论。分析的过程使用R语言完成。

进行基于随机森林的模型分析时，应用了R语言的功能包Boruta。Boruta包对随机森林进一步改进，通过在系统中加入随机性，然后从随机样本集中收集结果，减少随机波动和相关性的误导影响。计算时，设定树的数量为500进行计算。

Lasso回归使用R中的glmnet包进行计算。通过改变正则项的 值，获得模型的相对误差值。在第二步选取合适的 值，考虑相对误差值较小的参量，同时结合专业分析后确定的合适的变量数量进行建模。经过计算，相对不重要的变量系数将变为零，相对重要的变量将保留在模型中，从而达到变量筛选的目的。

本文从公开发表的文献中选取了一系列数据。选择的原则有以下几点：首先，在模型中有足够的自变量种类；其次，具有一定的样本量，可使模型更加稳定；第三，选择不同地区的数据，达到横向比较的目的。经过文献检索与分析，选取了五组煤矿的数据，分布于山西潞安[11]，安徽淮南[12]，安徽淮南[19]，河南郑州[20]，以及河南鹤壁[23]。

2 煤层瓦斯含量影响因素分析

以潞安矿区的数据为例。原始数据中含有的参数有埋深、基岩厚度、煤的水分、顶板岩性、底板岩性、离正断层平距、煤挥发分、煤层厚度、煤的灰分共九个参量。表1所示为文献部分数据。应用随机森林的方法得到各参量预测煤中瓦斯含量重要性排序如图1所示。应用Lasso回归的方法得到的重要性排序如图2所示。

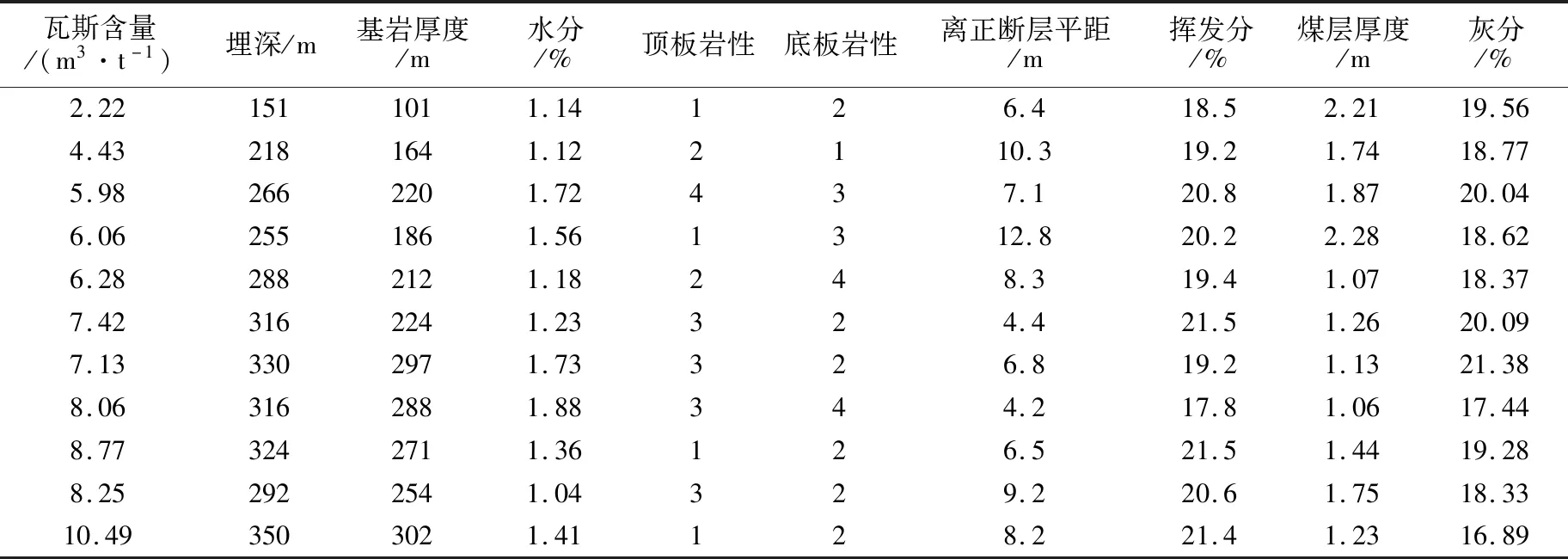
表1 煤层瓦斯含量与影响因素参数[11]

如图1所示，随机森林的分析结果显示煤层的埋深及基岩厚度对煤层瓦斯含量的重要程度显著高于其它因素，其次为煤层自身的地质参数，包括煤厚、灰分、挥发分等，而顶底板的岩性、距正断层的距离、煤层的含水量的影响程度较低。图2所示的模拟Lasso回归中，随着λ的增大，模型中参量的数量随之减少，但模型均方误差在增大。图中虚线的范围是模型误差最小的λ与一倍标准差范围内的λ值。综合考虑模型的稳定性与预测误差，被纳入模型的自变量有四个，分别是基岩厚度、埋深、煤的灰分与挥发分。

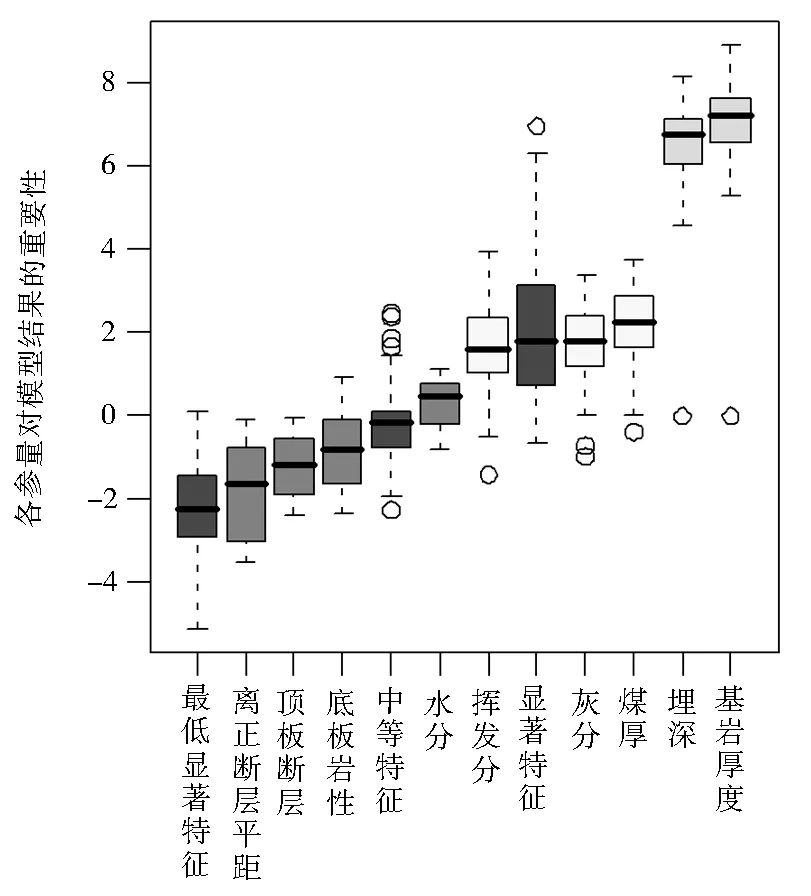
图1 随机森林分析煤层瓦斯含量影响因素排序

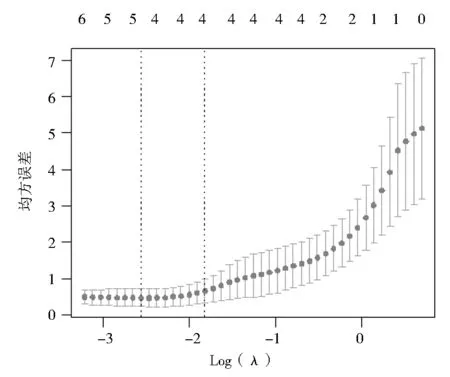
图2 Lasso回归不同λ值对应的相对误差与变量个数

另外几组数据也通过随机森林与Lasso回归的方法对预测的重要性进行了分析，分析结果如表2所示。

表2 煤层瓦斯含量影响因素的特征选择结果

从几组数据的分析结果看，多数研究选择了煤层埋深，基岩厚度，煤的物理、化学性质及煤层顶底板的性质等指标。对瓦斯含量影响最大的因素大部分是煤层埋深及基岩厚度，其它因素因地点的不同而有所区别，其中煤层倾角影响一般较小，煤的物理、化学性质以及主断层断距等指标在不同的模型中表现出不同的特征。

3 结 语

应用随机森林与Lasso回归分析了全国五处煤矿的数据，计算了各种地质因素对煤层瓦斯含量预测的重要性。从分析结果，可以得到以下几点结论：

1) 不同地区表现出类似的规律，即煤层埋深与基岩厚度对煤层瓦斯预测相对最重要。

2) 在不同的研究中，参数的选择方式差别较大，虽然埋深与基岩厚度的重要性是普遍的认识，但是其它因素的影响程度并未有统一的认识。在进一步的研究中，需要建立分析问题的标准方法，或相对统一的方法。

3) 不同地区的模型有所区别，特定地区的模型中影响因素也会有所差别。目前所选取的数据及模型数量有限，参数选择各异，数据量也较小，并不一定能代表各地的差别。要想评价一地模型的可泛化性，需要进行更加严格的实验设计，以及模型分析。

4) 在具体的建模过程中，多元回归仍是常用的建模方法之一，但在这个过程中应该特别注意的是变量之间的多重共线性。在本文的建模中，煤层埋深与基岩厚度都是瓦斯含量的重要影响因素，但这两者之间具有很强的相关性。在多元线性模型中会影响模型的稳定性，使模型失去解释能力。解决多重共线性的方法一般有专业判断，预先选择重要的变量，或者通过主成分分析将相关的自变量用新的综合变量表示。再就是本文用到的正则化回归，也可以有效地降低多重共线性的影响。类似的，在支持向量机与神经网络的分析中，多重共线性也会对分析结果造成影响，在应用这一类方法建模时也应考虑到变量选择的问题。