1960-2017年珠江流域下游径流年际与年内变化特征
2019-12-11杨远东王永红蔡斯龙
杨远东,王永红,蔡斯龙,刘 锋
(1.海底科学与探测技术教育部重点实验室,中国海洋大学 海洋地球科学学院,山东 青岛266100;2.广东省水文局,广州 广东510150;3.中山大学 海洋科学学院,广州 广东510275)
河川径流年际变化与年内变化特征对于河道整治、农业灌溉、工农业用水、水库调水等方面意义重大。分析径流年际、年内特征的方法较多,例如白丽等[1]使用径流变差系数(Cv)法对1957—2015年赣江流域径流特征及变化规律分析,戴明龙等[2]对长江流域1952—2006径流时空分布及变化规律进行了研究。杨敏等[3]使用M-K 趋势检验法对1951—2015年洞庭湖水沙演变进行了评估,李瑞等[4]使用此方法对渭干河流域1960—2006年径流量进行了研究,除此之外,常用的方法还有R/S 分析法[5-7],丰枯等级划分法[8-9],滑动平均法[10-11]等。径流年内分析主要方法有集中度(期)法[12-13],年内分配不均匀系数法[14]等。
这些方法在研究珠江流域径流变化时也经常使用,例如吴创收等[15]对近100年来珠江流域西江年径流量进行了研究,发现其存在着2~3 a,12 a左右以及27 a左右的振荡周期;陈立华等[16]对珠江流域西江1980—2010年径流进行了分析,发现西江下游水文站径流存在不显著的下降趋势;李艳等[17]对珠江流域北江1956—2000年径流进行了分析,发现年径流量系列呈不显著缓慢上升趋势,并存在2年左右的变化周期;刘金凤等[18]对珠江流域东江1956—2015年径流进行研究,发现近60 a东江流域年径流变化趋势总体平稳,未有显著变化。这些研究往往只集中在某一流域,研究的内容也仅仅对径流年内变化或年际变化单独研究,未能将其综合对比。本文采用径流年际变差系数(Cv)、年际极值比(W)、M-K 趋势分析、滑动平均法、Morlet小波分析法、集中度(期)等方法对珠江流域西江(高要)、北江(石角)、东江(博罗)水文站1960—2017年径流进行分析,以期更好理解近几十年内其年际与年内变化特征。
1 材料与方法
1.1 研究区概况
珠江发源于云南省马雄山,由西江、北江与东江3大支流构成,全长2 400 km,流域面积45×104km2,流经云南、贵州、广西、广东、湖南、江西6 个省(区)和越南的北部,是中国第二大河,境内第三长河。珠江流域地处亚热带,北回归线横贯流域的中部,气候温和多雨,多年平均温度在14 ℃~22 ℃之间,多年平均降雨量1 200~2 200 mm,多年平均径流量3.10×1011m3多(1954—2016年),多年平均输沙率2.80×107t多(1954—2016年),径流水沙季节分配很不均匀,常年4—9月份洪水期多年平均径流量约占全年的80%,输沙率占91~95%。珠江流域西北两江分别在广东省三水市思贤滘东西两侧、东江在广东省东莞市石龙镇汇入珠江三角洲。高要(112°27′13″E,23°2′43″N)、石角(112°56′59″E,23°33′39″N)、博罗(114°17′42″E,23°9′50″N)分别为进入三角洲之前西、北、东江最主要的水文控制站。
1.2 数据来源
本文收集了珠江流域进入珠江三角洲之前西、北、东江的主要水文控制站高要、石角、博罗1960—2017年月度径流量数据,长时间序列径流数据来源于广东省水文局,中山大学与《中国河流泥沙公报(http:∥www.mwr.gov.cn/)。珠江流域主要大坝建设数据来源于中国大坝工程学会网站(http:∥www.chincold.org.cn/)。高要、石角、博罗水文站历史位置未发生改变,同时对3站径流年际累计值进行分析,分析结果如图1所示。3站径流年际累计值基本为一条直线,其相关系数R 值接近1,径流分析结果表明3站径流数据一致性较强。

图1 1960-2017年高要、石角、博罗水文站际累计径流量
2 结果与分析
2.1 径流年际变化特征
2.1.1 径流年际变异性 河川径流量的年际变化主要取决于降水量的年际变化,同时还受流域水源补给类型及流域内地貌、地质等条件的影响[19],径流年际变异性常用变差系数(Cv)与年际极值比(w)来表示,变差系数(Cv)是水文统计中的一个重要参数,用来说明水文变量长期变化的稳定程度[20],其值为样本序列的标准差与算术平均值的比值,Cv值越大,年径流量的年际变化越大,是反映径流年际变化不均匀性的重要指标[21-22]。变差系数(Cv)计算公式如(1)[23]:

式中:ki——模比系数,即第i年的年径流量与平均年径流量的比值;n——系列长度。
年际极值比(w)是指径流量变化的绝对值比例,其大小用多年最大、最小年径流量比值表示[24],年际极值比计算公式如(2)[23]:

珠江流域西、北、东江1960—2017年径流年际变化特征值计算结果见表1。由表1可知,西、北、东江径流变差系数(Cv)值均较小,其值介于0.196~0.273之间,说明珠江流域径流年际变率较小,径流量稳定性较高,稳定性的大小顺序为西江大于北江大于东江。西、北、东江径流变差系数(Cv)与径流年际极值比(w)变化趋势相似,径流年际极值比(w)值介于2.398~4.636之间,西江w 值较小,北江、东江w 值较为接近且较大。径流变差系数(Cv)值与径流年际极值比(w)均反映1960—2017年珠江流域径流量年际变异程度东江高于北江高于西江。

表1 1960-2017年珠江流域西、北、东江径流年际变化特征
2.1.2 径流年际趋势性 用于诊断连续水文序列趋势性方法较多,其中应用最广范、最为简便直观的方法为M-K 趋势分析法与滑动平均法,本文分别用这两种方法对珠江流域西、北、东江1960—2017年径流趋势性进行分析。M-K 趋势分析法(Mann-Kendall法)是一种非参数统计检验方法,其优点是样本不需要遵循一定的分布,也不受少数异常值的干扰,更适用于类型变量与顺序变量,计算也比较简便,最初由曼和肯德尔提出原理并发展了这一方法。现已成为世界气象组织推荐并已广泛使用的非参数检验方法,适用于水文、气象等非正态分布的数据。其计算公式如公式(3)—(6),设径流序列为x1,x2,…,xn,Sk表示第i个样本xi>xj(1≤j≤i)的累计数,

其中:
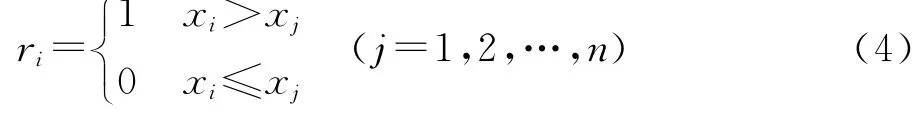
在时间序列随机独立的假设下,Sk的均值与方差分别为:
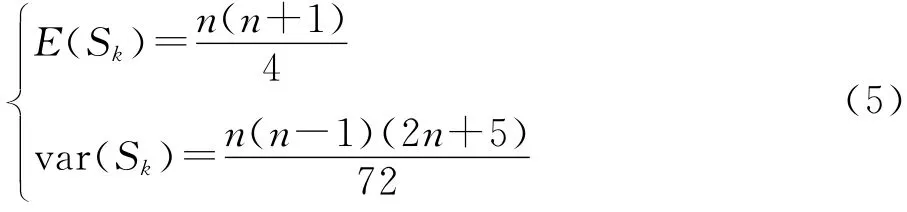
将Sk标准化为:

式中:UF1=0,给定显著性水平α,若|UF|>Uα,表明序列存在明显的趋势变化。将此方法引用到反序列,序列顺序变为xn,xn-1,…,x1,反序列标准化由UBk表示,UBk和UFk可组成2条曲线,在这里设定α 值为0.05,临界值U0.05为±1.96。
珠江流域西、北、东江1960—2017 年径流M-K趋势分析结果如图2所示。西江高要水文站1960—2017年UF与UB 统计曲线在信度区间内发生了5次交叉,根据统计学检验意义,1964,1986,1991,1999,2016年是高要水文站径流可能的突变年份,其中,UF值并未突破0.05置信区间,说明径流有上升、下降趋势但趋势不明显;北江石角站1960—2017 年UF与UB 统计曲线在信度区间内发生了6次交叉,可能 的 突 变 年 份 分 别 为1961,1973,1984,1990,1999,2016年,但UF 值未突破0.05置信区间;东江博罗水文站1960—2017年UF与UB统计曲线在信度区间内发生交叉次数较多,根据图像性质推测可能突变的年份分别为1963,1990,1999,2007,2017 年,UF值同样未突破0.05置信区间。综合分析,1960-2017年珠江流域西、北、东江支流径流虽存在各自的上升下降突变点,但UF值均未突破0.05置信区间,径流有轻微变化但总体变化趋势并不显著。

图2 1960-2017年高要、石角、博罗水文站径流M-K 检验
滑动平均法因其简单直观性,在水文学研究中应用较为广泛。其主要思路是将时间序列x1,x2,…,xn的几个前期值和后期值取平均,求出新的序列yt。其计算公式如公式(7)[25]:
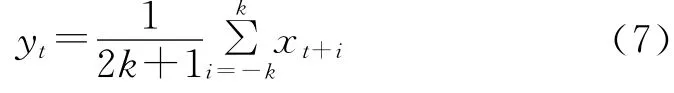
式中:yt——新序列;k 为滑动平均尺度;xt+i——参与此次生成新序列的旧序列值;k=1时yt为3 a滑动平均值,k=2时yt为5 a滑动平均值;若Xn有趋势性,选择合适的k,即可通过 将其趋势清晰地表示出来。
本文计算了珠江流域高要、石角、博罗1960—2017年径流3 a滑动平均值与5 a滑动平均值,计算结果如图3所示。
3个水文站3 a滑动平均值与5 a滑动平均值相差不大,均可说明径流的变化趋势。总体看来,径流都呈现上升—下降—上升—下降—上升5 个变化过程。高要水文站存在3 个上升期,分别为:1960—1970,1990—1997,2010—2017 年,且以后两个阶段上升速率较快,其余时段径流呈下降趋势,主要的变异年份为1964,1970,1988,1997,2011年;石角水文站同样存在3个上升期,分别为:1965—1975,1990—1997,2010—2017年,3个阶段上升速率差异不大,其余时段径流呈下降趋势,主要的变异年份为1964,1975,1983,1990,1998,2010 年;博罗水文站上升—下降阶段较为复杂,以6~8 a为时间间隔上升—下降相互交替出现,主要变异年份为1964,1975,1984,1990,1999,2003,2008年。

图3 1960-2017年高要、石角、博罗水文站年径流及3 a,5 a滑动平均
分析1960年以来西、北、东江突变点出现的原因,推测主要是由大洪水的出现导致,西江在1968,1986,1994,1998,2005,2016 年爆发过大洪水,北江在1968,1982,1994 年爆发过大洪水,东江在1984,2007,2016年爆发过大洪水,一般在洪水发生前后2 a内出现突变点。此外东江由于径流小而水库库容较大,人类对于水库的储放水活动也容易产生突变点。
对M-K 趋势分析法与滑动平均法检测出的突变点进行对比,结果如表2所示,两种方法检测出的突变时刻相差不大,滑动平均法检测出的突变点往往更多,但在两个时间端点(1965 年之前与2010 年以后),滑动平均法由于两端点数据缺失(3 a滑动平均只能输出1961—2016年数据,5 a滑动平均只能输出1962—2015年数据)检测性能往往较差,而M-K 趋势分析法不受端点限制,检验出3个水文站在时间轴右端点2016年左右均发生突变。

表2 高要、石角、博罗水文站M-K 检验与滑动平均法突变点对比
此外,对高要、石角、博罗3个水文站1960—2017年径流数据作线性回归分析,研究其58 a间总体变化特征,线性回归方程如图3所示,高要、石角、博罗线性分析斜率k值分别为-0.16,0.95,0.35,相关系数r值分别为0.002,0.047,0.03,根据线性回归计算结果分析可知,西江流域径流总体呈下降趋势,北、东江流域径流总体呈上升趋势。当α=0.05,n=58时,查表得相关系数r=0.259,3 个流域|r|值均小于r0.05,由此证明3个支流虽存在上升或下降趋势,但变化趋势并不明显。
2.1.3 径流年际枯丰变化 为找出径流序列丰、枯水年阶段性变化规律,根据水利部信息中心编制的水文预报规范,将径流量距平百分率Ki划分为5个级别,5个级别分别是:Ki<-20%为枯水,-20%≤Ki<-10%为偏枯,-10%≤Ki≤10%为平水,10%<Ki≤20%为偏丰,Ki>20%为丰水。其中Ki计算公式如公式(8):

珠江流域西、北、东江控制站高要、石角、博罗3个水文站年径流距平百分率Ki计算结果如图4 所示,年径流分级统计结果见表3。3个水文站径流丰枯差异较大,高要、博罗站平水年所占比例最大,1960—2017年平水年所占比例分别为37.9%,44.8%,石角站丰水年所占比例最大,1960—2017年丰水年所占比例为48.3%,接近调查年份总年数的一半。1960—2017年高要水文站丰水年与偏丰年总计18 a,而枯水年与偏枯年总计也为18 a,其平水年比例占比最大,说明西江流域旱涝灾害发生较均匀且发生率较低,水情较为稳定;石角水文站丰水年与偏丰年总计31 a,枯水年与偏枯年总计9 a,丰水年比例远远高于枯水年,且丰水年比例也高于平水年,说明北江流域易发生洪涝灾害;博罗水文站丰水年与偏丰年总计16 a,而枯水年与偏枯年总计也为16 a,且其平水年所占比例最大,说明东江流域旱涝灾害发生较均匀且发生率较低,水情比较稳定。按此方法分析西、北、东江旱涝灾害发生率最小的为西江、其次为东江,最易发生旱涝灾害的为北江。
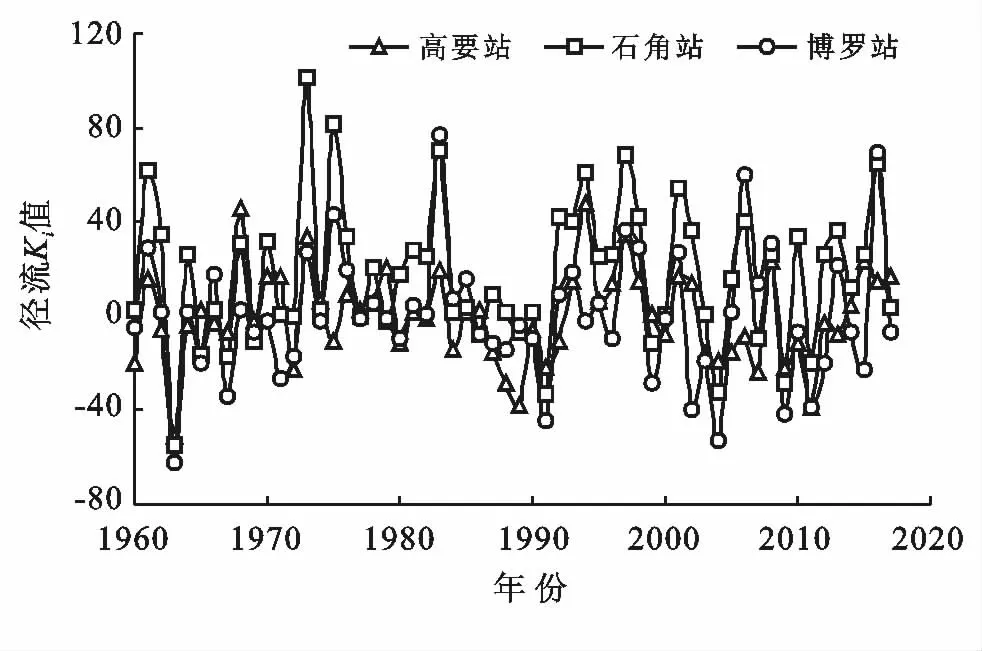
图4 1960-2017年高要、石角、博罗站径流距平百分率K i 值

表3 1960-2017年珠江流域高要、石角、博罗水文站年径流分级统计
高要、石角、博罗3个水文站径流量距平百分率Ki在不同年代之间也存在差异,高要水文站丰水年主要发生在1965—1975,1994—1998年期间,枯水年主要发生在1987—1992年期间;石角水文站主要发生在1965—1977,1990—2016 年期间,其中1990—2016期间也是枯水年多发年份;博罗水文站丰水年、枯水年多发的年份都为1990—2016年,丰枯年份基本交替出现。
2.1.4 径流年际周期性变化 本文采用Morlet小波分析对珠江流域西江、北江、东江支流1956—2013年径流量进行周期性分析。Morlet小波能从时域和频域两方面进行信号分辨,能够准确地揭示隐藏在时间序列中的多种变化周期,充分反映出系统在不同时间尺度中的变化趋势。Morlet小波分析计算公式如公式(9)—(10)。对于给定的能量有限信号f(t)∈L(R),其连续小波变换为:

式中:Wf(ɑ,b)——小波变换系数;f(t)——一个信号或平方可积函数;ɑ,b∈R;ɑ≠0,ɑ 为伸缩尺度;b——平移参数。将小波系数的平方值在b 域上积分,得小波方差如下式:
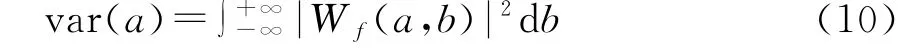
根据公式计算得出珠江流域流域西、北、东江小波系数实部等值线见图5。小波系数实部等值线图能反映径流序列不同时间尺度的周期变化及其在时间域中的分布。
根据图5可知,珠江流域西江径流存在25~32 a,15~20 a,3~8 a这3类尺度的周期变化特征;北江径流存在25~32 a,10~20 a,4~10 a这3类尺度的周期变化特征;东江径流存在25~32 a,10~20 a,4~7 a这3类尺度的周期变化特征。3个支流均存在25~32 a的周期变化,58 a间西、北、东江分别出现6,5,5次周期震荡,该时段的周期变化较为稳定,具有全域性;第二震荡周期基本为10~20 a,西、北、东江分别出现9,11,12次周期震荡;第三震荡周期基本为4~10 a,西、北、东江震荡次数较多,平均每2~3 a就会出现一次丰季或枯季。
2.2 径流年内变化特征
本文借鉴径流量年内分配的向量法定义单站径流时间分配特征的参数径流集中度和集中期。径流集中度指各月径流量按月以向量方式累加,其各分量之和的合成量占年径流量的百分数,其意义是反映径流量在年内的集中程度。集中期是指径流向量合成后的方位,反映全年径流量集中的重心所出现的月份,以12个月分量和的比值正切角度表示,具体计算过程见刘贤赵等[12]文献。计算公式如公式(11)—(13):
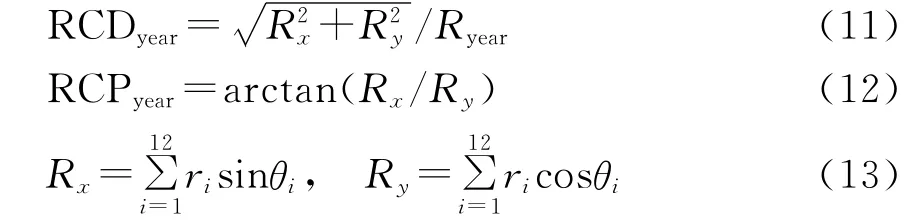
式中:RCDyear——年径流集中度;RCPyear——年径流集中期;Ryear——年径流量;Rx,Ry——12个月的分量之和所构成的水平、垂直分量;ri——第i月的径流量;θi——第i月径流的矢量角度。RCDyear越大表示径流量越分散,越小径流量越集中,RCPyear表示一年中最大径流量出现的时间,表4为各个月份包含及代表角度值。

图5 1960-2017年高要、石角、博罗水文站径流小波分析实部等值线
珠江流域高要、石角、博罗水文站1960—2017年间10 a尺度的径流集中度与集中期计算结果如表5所示。从径流集中度的大小关系可以看出西江年径流量的分散程度略高于北江,高于东江。根据年径流集中期对应的角度,发现西江最大径流量主要出现于7月份,北江最大径流量主要出现在5,6 月份,东江最大径流量主要出现6,7月份。
RCDyear与RCPyear在1960—2017 年也表现出一定的变化趋势,1960—2009 年间年径流集中度较为相似,2010—2017径流集中度明显减小,尤其以西江高要水文站减小最为剧烈,反映了最近10 a间径流年内分配变得更加分散。而对于年径流集中期,各个水文站变化具有不一致性,高要水文站径流集中期对应角度虽都位于165°~195°之间,但径流集中期对应的角度呈减小趋势,反映了西江最大径流月份不变,但在最大径流月内最大径流日期向前移动;石角水文站径流集中期对应角度无明显增大或减小趋势,上下震荡,1980—1989年径流集中期为5月份,其余时间径流集中期为6月份;同石角水文站相似,博罗水文站流集中期对应角度也属于上下震荡类,1980—1989,2010—2017年径流集中期为6月份,其余时间径流集中期为7月份。
同时,对1960—2017 年高要、石角、博罗水文站月度径流作等值线图(图6),从图6中可以清楚地看出径流年内的分散程度与最大、最小径流出现的时间。对比径流等值线图与径流集中度与集中期表格,发现其演变阶段具有一致性,径流等值线图年内径流较分散年份,径流集中度往往也较低,反之亦然,而径流集中期角度的波动与等值线图最大值的上下移动也有较好的对应性。
图6 1960—2017高要、石角、博罗水文站径流等值线

表4 RCPyear计算各月份包含及代表角度值 (°)
3 讨论
3.1 径流年际变化
本文从变异性、趋势性、周期性与丰枯变化特征等方面说明了珠江流域下游主要水文站西江高要站、北江石角站、东江博罗站径流年际变化特征。其中变异性、丰枯变化特征反映了径流的年际波动特征,即反映径流的稳定性,综合变异性与丰枯变化特征,珠江流域下游径流变异性与丰枯变化最小的都为西江,其径流稳定性最高,而北江、东江在变异性与丰枯变化两个特征方面排序不同,在变异性方面,东江虽高于北江但两者径流年际变差系数(Cv)、年际极值比(w)数值都较为相近,而在丰枯变化特征方面,北江变化程度远远高于东江,综合两方面,认为东江稳定性高于北江,稳定性由大到小为西江、东江、北江,且三江都基本存在25~32 a,10~20 a,4~10 a的径流周期变化。而在径流趋势性方面,3个水文站虽存在众多变异点,但由于M-K 分析均为突破0.05 置信区间,且线性回归|r|值均小于r0.05,证明径流无明显趋势性。

表5 高要、石角、博罗水文站年径流集中度与集中期
分析径流年际变化的原因,流域降水的多少对于径流影响巨大[26],特别是在人类活动影响较小的地区,其作用更为显著,降水通过影响流域水分在下垫面的垂向和横向的再分配,进而作用于流域径流的变化[27]。除此之外,流域植被覆盖率也是影响流域径流的因素之一,但在珠江流域,其对径流变化的贡献并不显著[28]。
受距离海洋的远近及海拔的影响,珠江流域西北部长期降水分布较平均,降水极值情况发生的几率相对较低;东南部长期降水较集中,降水极值情况发生的几率相对较高[29]。受降水空间分布特征的影响,西江径流较为稳定,东江、北江相对较差。除自然因素外,人类对于径流年际变化也有一定的影响,但相对于自然作用其影响程度较小,人类主要通过流域修建大坝、影响流域植被覆盖率等方式影响流域径流,在珠江流域,大坝的修建是人类的主要作用方式,例如由于东江径流量较小,且其水库库容较大(见表6),在新丰江水库等的调节作用下,径流稳定性得到改善,较少发生大洪水或极端干旱,而北江径流量大于东江,水库库容也较东江较小,人类干预作用较小,稳定性较差。
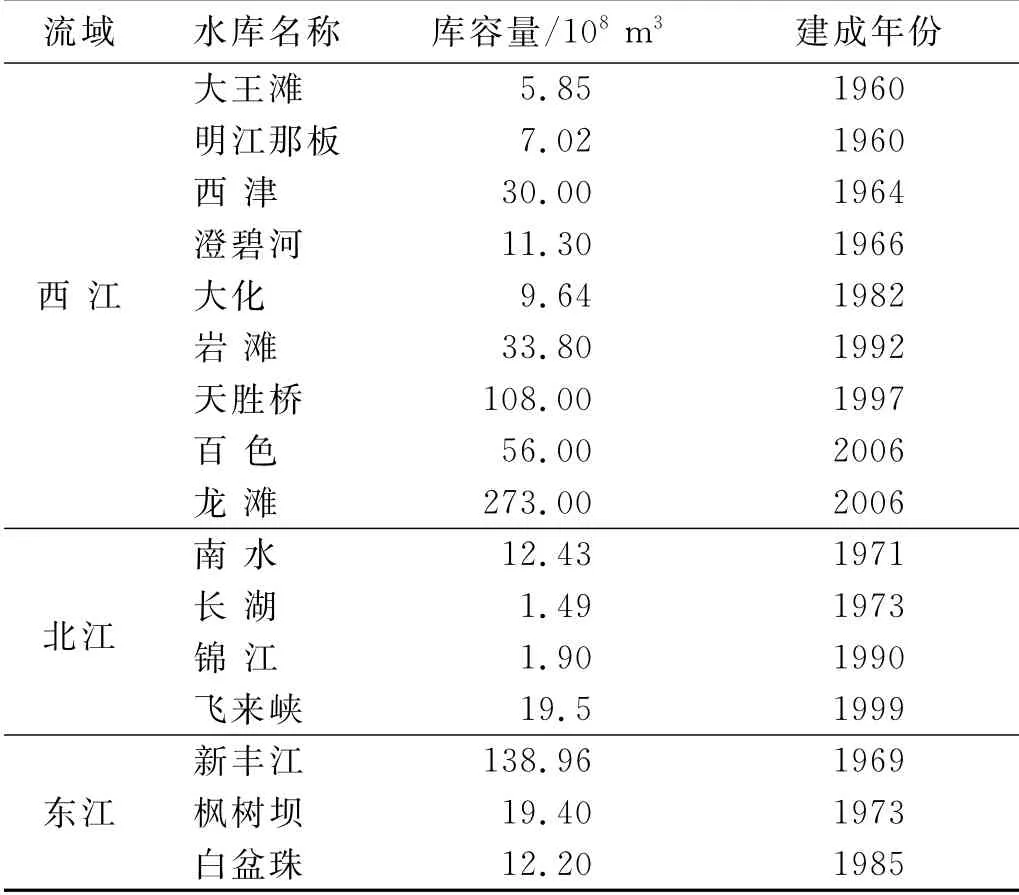
表6 珠江流域较大规模水库建设情况
3.2 径流年内变化影响因素
上文通过集中度与集中期分析了西江高要站、北江石角站、东江博罗站径流年内分配情况,研究结果表明,径流集中度总体呈下降趋势,西江、东江下降速度较快,其下降时期分别为2010—2017,1970—1979年,北江下降速度较慢,主要下降期为2010—2017年,径流集中度的下降与流域水库修建等人类活动关系密切,人类活动一般通过建设各类水利工程、变更土地利用类型等改变下垫面条件来间接影响流域径流[30],且其对于径流年内的影响程度远高于年际,例如通过水库、淤地坝、水窖等蓄水工程,拦蓄地表径流、消减洪峰流量、调节径流分配。目前,在对中国众多流域的研究中都发现,人类活动对于流域径流量变化的贡献率都远远超过50%[31-33]。
水库的修建延长了汇流时间,消减了洪峰,使年内流量过程线变得平缓。20世纪60年代,大规模的水库尚未建成,此时径流集中度可近似代表原始状态下的年内径流集中程度,集中度主要受各个流域降水的影响,其由高向低依次为西江、北江、东江,2010—2017年处于人类的剧烈活动下,众多水库已建成或正在修建,这一阶段径流集中度由高到低依次为北江、西江、东江,2个阶段西江、北江、东江径流集中度的变化比例分别为23%,11%,28%,而计算目前三江水库库容所占径流量比例,分别为25%,8%,72%,两者大小关系较一致,说明了大坝修建在调节径流年内分配方面有重要作用。
与径流集中度相似,径流集中期同样受人类活动影响,20世纪60年代珠江流域受人类活动影响较小,径流主要受降水控制[34],由于各个流域间气候存在差异,造成北江最大径流出现时间早于东江早于西江,受人类活动的影响,1960—2017年间径流集中期有向前移动的趋势,但目前各个支流年内最大径流出现的时间仍为北江早于东江早于西江。
4 结论
本文基于珠江流域西、北、东江主要控制站高要、石角、博罗水文站1960—2017年月度径流数据,利用径流年际变差系数(Cv)、年际极值比(w)、M-K 趋势分析、滑动平均、集中度(期)等方法对三站长序列径流年际变化与年内变化特征进行研究,主要结论如下:
(1)珠江流域西、北、东江径流变差系数(Cv)值均较小,其值介于0.196~0.273之间,说明珠江流域径流年际变率较小,径流量稳定性较高,流变差系数(Cv)与径流年际极值比(w)均反映珠江三条支流年径流稳定性顺序西江>北江>东江。
(2)M-K 趋势分析法与滑动平均法均检测出珠江流域径流存在若干突变点,径流有轻微变化但总体变化趋势并不显著。
(3)径流丰枯变化表明西、东江流域旱涝灾害发生较均匀且发生率较低,北江流域易发生洪涝灾害。
(4)Morlet小波分析表明,近几十年珠江流域西、北、东江径流普遍存在25~32 a,10~20 a,4~10 a的周期变化。
(5)珠江流域径流年内分配极不均匀,年径流集中度(RCDyear)西江略高于北江,高于东江,且近年来集中度都有减小趋势;年径流集中期(RCPyear)表明西江最大径流量主要出现于7月份,北江最大径流在5,6月份交替,东江最大径流量在6,7月份交替出现,近年来集中期都有向前(更早月份)移动趋势。
