卷积核归一化
2019-12-11李宏亮郝子宇
王 迪,许 勇,李宏亮,郝子宇
(江南计算技术研究所,江苏 无锡 214083)
0 引 言
近年来,深度学习(deep learning)凭借其强大的学习能力和分类能力在图像分类、目标检索、语音识别和自然语言处理等任务中得到了广泛应用,是目前人工智能领域发展的核心[1-2]。但是随着网络的加深,深度神经网络的训练愈加困难。在训练网络的过程中,前层参数的调整会导致之后每一层的输入分布发生变化,并随着每层参数放大或缩小,使得训练收敛变慢。Sergey等将这一现象称为内部协方差位移(internal covariate shift,ICS)[3]。一般有以下几种办法缓解该问题:
(1)调整初始化参数,例如使用Xavier[4]对权重进行初始化,使输出和输入尽可能服从相同的分布;
(2)对神经元进行Dropout[5],消除减弱神经元节点间的联合适应性,增强泛化能力;
(3)使用归一化层,例如使用批量归一化(batch normalization,BN)[3]对激活值进行操作,防止参数的微小变化在网络中放大。
通常情况下,以上解决方法会组合使用。归一化技术一经提出,作为解决该问题最有效的方法之一,得到了广泛的关注和研究,已经在各种深度神经网络中被广泛应用。例如,在进行图像分类和识别时,批量归一化通过计算批的均值和方差进行归一化,可以减少层与层协方差位移,使整个训练集的特征值保持在一个稳定的分布,加快训练收敛速度。但是批量归一化依赖于批的大小,当批过小时,批量归一化的效果大大下降。此外,批量归一化给整个网络增加了额外的计算量,需要更多的计算和存储资源。在测试时,由于批的大小为1,批量归一化使用的均值和方差来自训练集的滑动平均值,会产生一定误差。
文中提出了一种简单的归一化方法来解决内部协方差位移问题——卷积核归一化。卷积核归一化独立于批的大小,对权重的输出通道进行归一化,大大减少了计算量,且不需要存储归一化的中间量。通过数学证明和实验验证,卷积核归一化可以有效解决内部协方差位移的问题,相比批量归一化,减少了75%至81%的计算量。在批较小的时候,卷积核归一化准确率比批量归一化高0.9%至12%。在批较大时,卷积核归一化和批量归一化的最高准确率差不超过1%。
1 相关工作
归一化算法来自一种数据预处理的方法——白化(whitening/sphering)[6]:将输入数据线性映射成零均值、单位方差的非相关分布。对每层输入进行白化处理可以实现固定的输入分布,有效消除内部协变量位移的影响。但如果在训练时,每层网络都使用白化算法,计算量太大且不是处处可微的,所以要寻求一种简化的方式,既可以使每层的数据近似独立同分布,且在计算量上也是可接受的。
归一化算法基于白化处理,并对白化进行了简化,在一定维度上计算均值和方差,进行归一化。为了使数据不丧失原有特征,加入两个可学习的参数进行再缩放和再位移。归一化算法的计算公式可以归纳为:
(1)
其中,μ和σ是由输入x计算得到的归一化统计量;γ和β是学习参数,用于恢复模型的表达能力。
归一化算法可以使网络具有“伸缩不变”的特性。当权重或数据发生伸缩变换时,加入归一化层(如BN)可以使前向传播的特征值和反向传播的雅可比矩阵值保持不变。
当W'=λW时,前向传播的特征值为:
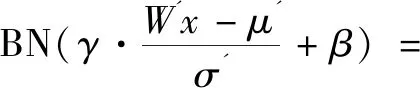
BN(Wx)
(2)
反向传播的雅可比矩阵值为:
(3)
2015年Sergey等提出批量归一化[3],有效解决了内部协方差位移问题,提高了训练收敛速度。但是,当批的大小过小或者每个批的数据没有充分混洗导致数据不是独立同分布时,一批数据的均值和方差不能代替整个训练集的统计量,批量归一化的效果会大打折扣。因此,Sergey等在2016年又对该算法进行了一些修改,提出了批量再归一化算法(Batch renormalization,BRN)[7],增加了两个滑动批常量来缓解批过小时的问题。层归一化(layer normalization,LN)[8]计算一层网络所有通道的均值和方差,对每个神经元训练自适应的缩放参数和位移参数,主要应用于循环神经网络(recurrent neural network,RNN)[9]。实例归一化(instance normalization,IN)[10]对单个图片进行归一化,保持实例之间的独特性,主要应用于图像风格迁移。组归一化(group normalization,GN)[11]通过对通道特征进行分组归一化。以上四种对特征值操作的归一化算法,都结合各自适用模型在批量归一化算法的基础上进行了部分优化,但其需要的计算和存储资源都等同或略大于批量归一化。权重归一化(weight normalization,WN)[12]通过对单个权重进行归一化来加快深度神经网络的收敛速度,在一定程度上减少了计算量,但准确率比批量归一化低,需要加入均值处理。
2 卷积核归一化
文中提出一种简单的归一化方法来解决内部协方差位移问题——卷积核归一化。卷积核归一化独立于批的大小,对权重值的输出通道进行归一化处理,大大减少了计算量,且不需要存储归一化的中间量。
卷积核归一化对权重值的输出通道进行归一化操作,可以直接将卷积层或全连接层前的数据分布传递到后面的卷积层或全连接层,从而有效减少内部协方差位移。卷积核归一化可以在减少计算量和存储的情况下,得到和批量归一化近似的性能。
2.1 算法描述
卷积核归一化运算过程如图1所示,‖wC‖F是权重值输出通道的欧几里得范数(Euclidean normalization)。在卷积层中,权重是一个四维张量:卷积核高(h),卷积核宽(w),输入通道(c),输出通道(C),‖wC‖F是在hwc维度上计算得到的C个范数;在全连接层中,权重是一个二维张量:输入通道(c),输出通道(C),‖wC‖F是在c维度上计算得到的C个范数。
输入:批量输入数据Batch={x1,x2,…,xn},批大小N
参数:权重参数W,学习参数γ,β
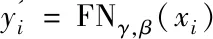
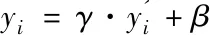
图1 卷积核归一化算法
设输入特征图为x,x∈Rm,x服从均值为0,方差为1的高斯分布,则有E[x]=0,D[x]=E[xxT]=I,I是单位矩阵。权重矩阵为W,W∈Rn×m。输出特征图为y,y∈Rn,则有:
y=Wx
(4)
y的自协方差矩阵为:
D[y]=E[(y-E[y])(y-E[y])T]
(5)
由于W和x是两个独立随机的变量,所以将式4带入式5,化简可得:
D[y]=E[WWT]
(6)
对W进行图1的卷积核归一化处理后,y的自协方差矩阵D[y]在权重矩阵W的行向量独立随机分布时等于单位阵I,此时则可以保证卷积层和全连接层前后的数据分布保持一致,不存在内部协方差位移。但是,权重矩阵W仅在初始化时可以保证其行向量之间是独立随机分布的,在训练过程中,W会随着模型的反向传播不断更新,所以在卷积核归一化过程中加入两个学习参数,对特征值进行再缩放和再位移以保持模型的泛化能力。
(7)
在反向求导的过程中,会出现向量对矩阵求导和矩阵对矩阵求导的情况,将矩阵向量化vec(X)=[X11,…,X1m,X21,…,Xn1,…,Xnm]T后可使用链式法。则卷积核归一化反向求导的计算过程为:
(8)
2.2 卷积核归一化与批量归一化
卷积核归一化旨在减少深度神经网络的内部协方差位移,达到与批量归一化相同的效果,在减少批量归一化计算量的同时,消除批大小较小或数据混洗不充分时批量归一化效果不佳的弊端。
以卷积神经网络为例,输入数据为一个四维张量:批(N),图片高(H),图片宽(W),输入通道(C),权重为一个四维张量:卷积核高(h),卷积核宽(w),输入通道(c),输出通道(C)。需要注意,进行卷积核归一化的权重输出通道等于进行批量归一化数据的输入通道。
根据批量归一化的运算过程,一批数据经过批量归一化的计算量(运算次数)为:
(9)
由于卷积核归一化的运算过程中包括卷积运算或全连接运算,所以在统计计算量时应去掉,即在正向传播时去掉权重矩阵W'与输入向量x的计算过程,在反向传播时去掉更新输入向量x残差的计算过程,去掉归一化后的权重矩阵残差更新的计算过程。卷积核归一化的计算量(运算次数)为:
(10)
则卷积核归一化相对于批量归一化减少的总计算量为:
(11)
结合经典的卷积神经网络结构、常用数据集和参数设置,卷积核归一化减少的计算量如表1所示。

表1 卷积核归一化相对批量归一化减少的计算量
从表1中可以观察到,随着网络的加深,卷积核归一化相对批量归一化算法减少的计算量越来越逼近19/23≈82%。这说明在网络越深的模型中,除了与批量归一化同样训练和更新学习参数γ和β外,卷积核归一化其余的计算量所占比越少。
3 实验结果与分析
3.1 数据集处理
文中针对深度神经网络中的图像识别任务重点进行了对比试验,使用cifar10数据集[13]和ImageNet数据集[14]。cifar10数据集共有60 000张彩色图像,图像大小为32×32,分为10类,每类6 000张图像,其中50 000张用于训练,10 000张用于测试,数据集大小为163 M。ImageNet数据集有1 400多万张彩色图像,涵盖2万多个类别。与ImageNet数据集对应的是ImageNet国际计算机视觉挑战赛(ImageNet large scale visual recognition challenge,ILSVRC),此次实验使用的是ILSVRC2012,分为1 000类,训练集有128万多张图像,测试集有5万张图像,数据集大小为141 G。
文中选择LeNet[15]和ResNet这两种典型的卷积神经网络进行实验。实验平台是两块Nvidia Tesla P100。
3.2 数据集预处理和参数设置
由于卷积核归一化依赖于输入数据的分布,所以需要对数据进行一些预处理。在训练过程中,为增加数据鲁棒性,对输入图片进行混洗和随机翻转、增强、裁减后,按批次进行归一化处理,减去一批输入数据的均值并除以方差,使得输入数据的分布在较深的网络中在卷积核归一化层的影响下传递初始数据分布,减少内部协方差位移。在测试过程中,由于没有批的存在,所以每个图像单独进行归一化预处理。
卷积核归一化使得网络在一些超参数的选取上需要谨慎。权重参数使用均值为0、方差为0.005的高斯分布进行初始化,并使用0.000 5的衰减系数进行指数衰减。学习率取0.01,每隔一定时间下降0.1。
3.3 实验一:cifar10+LeNet-5
LeNet-5是一个5层的卷积神经网络,包括3个卷积层和2个全连接层。权重使用高斯分布进行初始化,权重衰减使用指数衰减。学习率初始值为0.01,每100个epoch下降0.1,一共下降3次。批大小分别取8,32,128进行对比实验。cifar10的训练数据使用随机水平翻转、随机亮度对比度调整、随机剪裁增加训练集的鲁棒性。使用卷积核归一化时,输入图像按批进行归一化预处理。
如图2(a)所示,LeNet-5网络在使用批量归一化时,训练准确率收敛速度受批大小的影响较大,尤其在批大小为8时,收敛速度缓慢。如图2(b)所示,使用卷积核归一化的网络准确率收敛速度基本不受批大小的影响。特别地,在进行批大小为2的实验中,使用批量归一化的LeNet-5训练不能收敛。
两种归一化算法在不同批大小下的测试集准确率如表2所示。可以明显观察到批量归一化算法的准确率随批的增大而提高,而卷积核归一化算法的准确率不受批大小影响,在86.30%左右浮动。在批较大时,卷积核归一化和批量归一化可达的最高准确率相差不超过0.01%。
(a)批量归一化
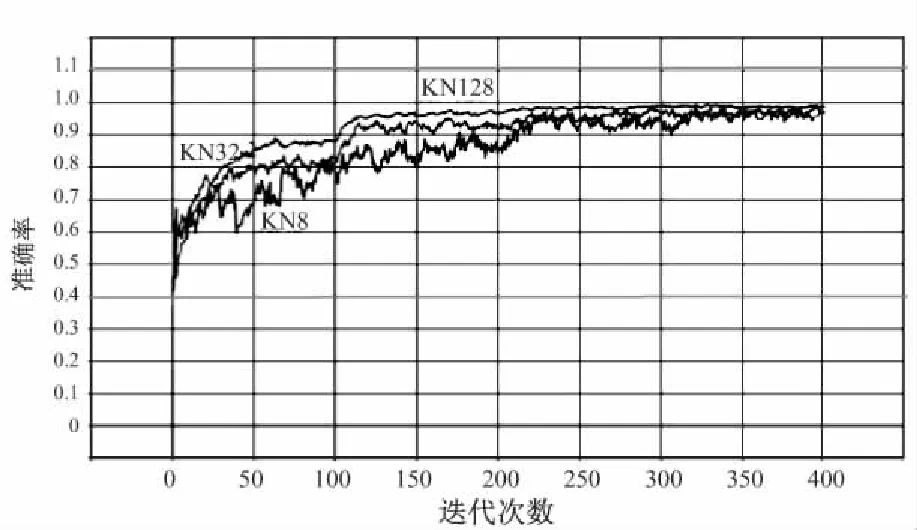
(b)卷积核归一化图2 cifar10+LeNet-5在不同批大小下的
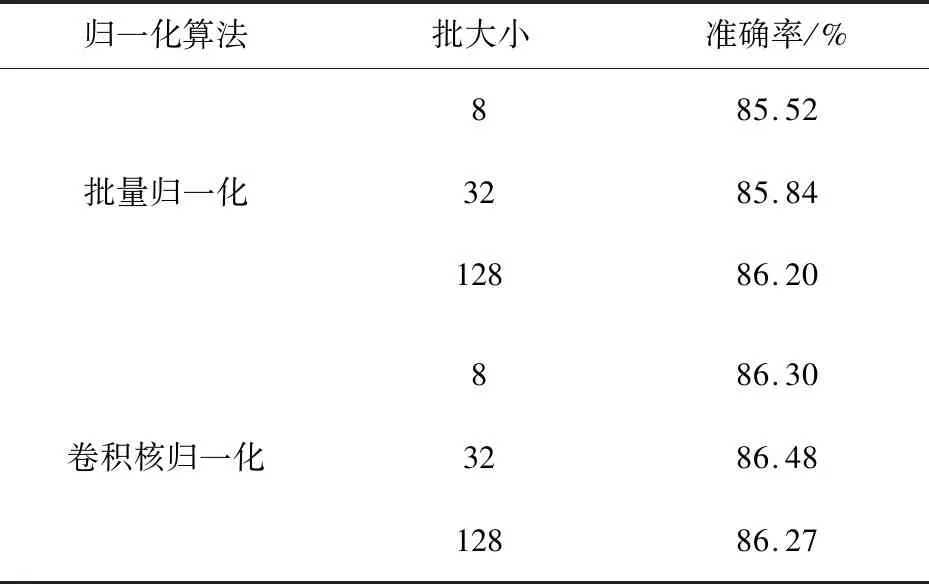
归一化算法批大小准确率/%批量归一化885.523285.8412886.20卷积核归一化886.303286.4812886.27
3.4 实验二:cifar10+ResNet20
ResNet是一种新的学习框架,使用残差映射加快模型收敛速度,得到更高的准确率。实验使用的ResNet20结构如表3所示。
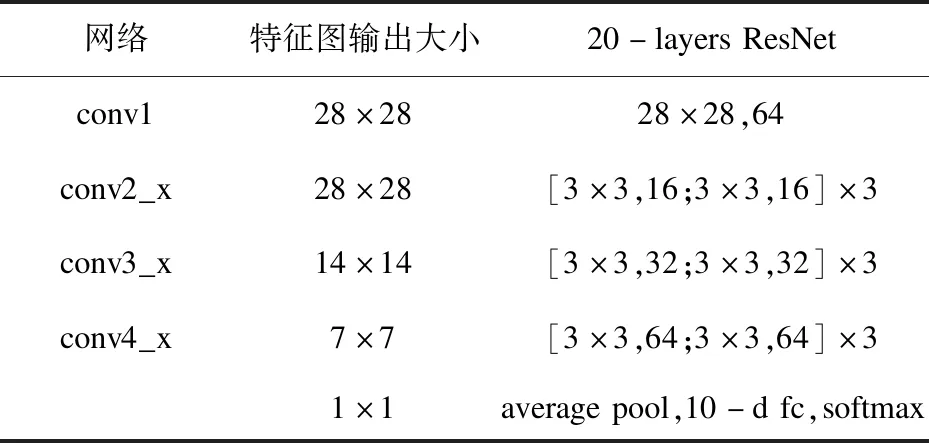
表3 ResNet20网络结构
权重值使用高斯分布进行初始化,权重衰减使用指数衰减。学习率初始值为0.01,每隔200个epoch下降0.1,一共下降3次。批大小分别取2,8,32和128进行对比试验。cifar10数据集的数据预处理同3.3节。

(a)批量归一化
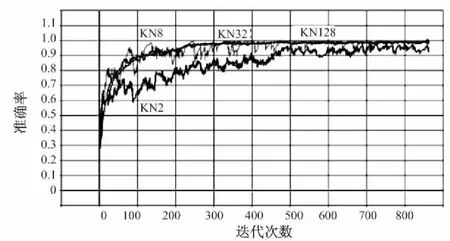
(b)卷积核归一化
从图3可以看出,使用残差网络可以较快地使训练准确率收敛。批量归一化在小批量,即批大小为2和8时准确率收敛速度较慢,准确率较低,而卷积核归一化基本不受批大小的影响。
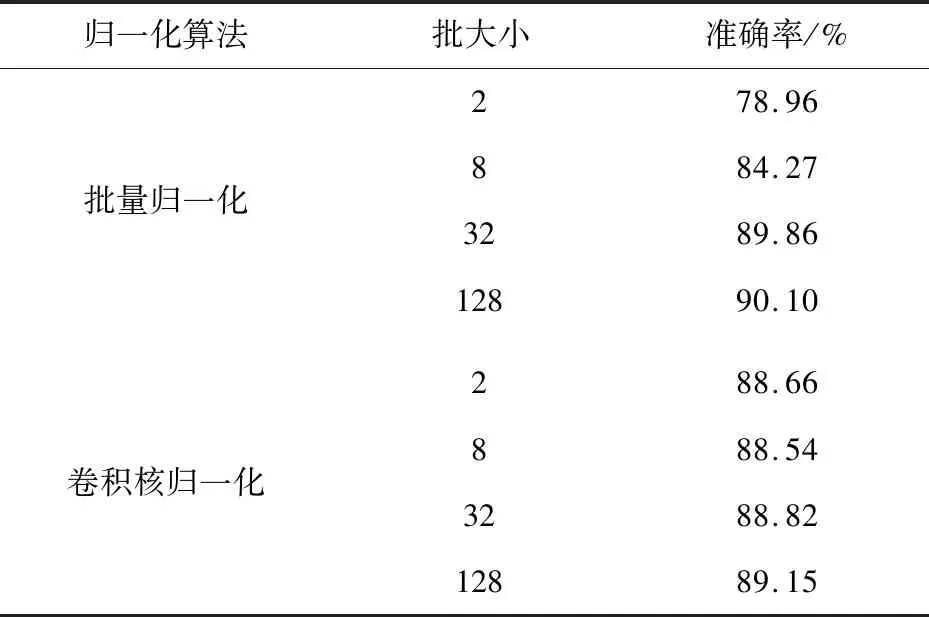
表4 cifar10+ResNet20测试集准确率
测试集准确率如表4所示,使用批量归一化算法的准确率随着批大小增大显著提高,而卷积核归一化算法的准确率不受批大小的影响。在批较小时,卷积核归一化比批量归一化的准确率高4%至10%;在批较大时,卷积核归一化准确率和批量归一化可达的最高准确率相差不超过1%。
3.5 实验三:ImageNet+ResNet50
本实验使用ResNet50,网络结构如表5所示。
权重使用高斯分布初始化,权重衰减使用指数衰减。学习率初始值为0.01,每15个epoch下降0.1,一共下降2次。批大小取64进行对比试验。ImageNet的训练数据使用随机剪裁、随机左右翻转等操作增强训练集的鲁棒性。使用卷积核归一化时,输入图像按批进行归一化处理。
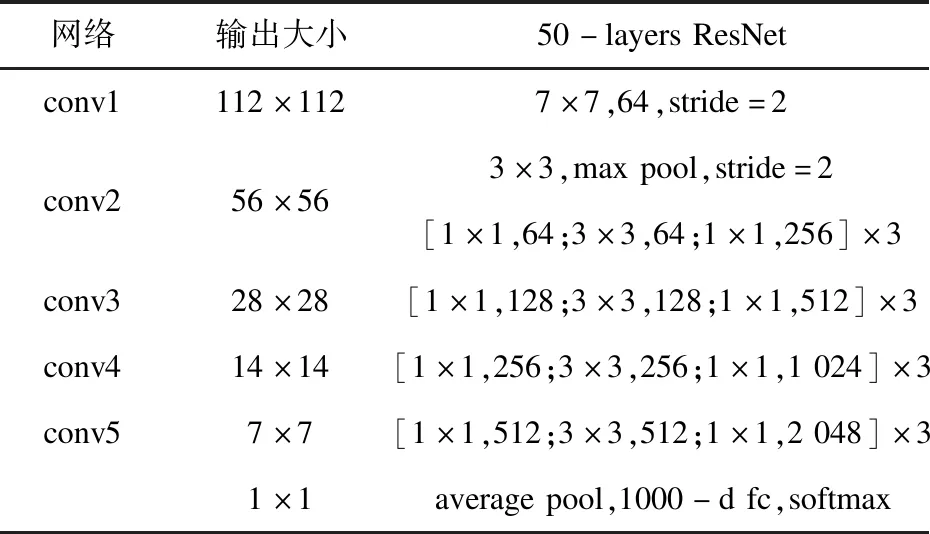
表5 ResNet50网络结构
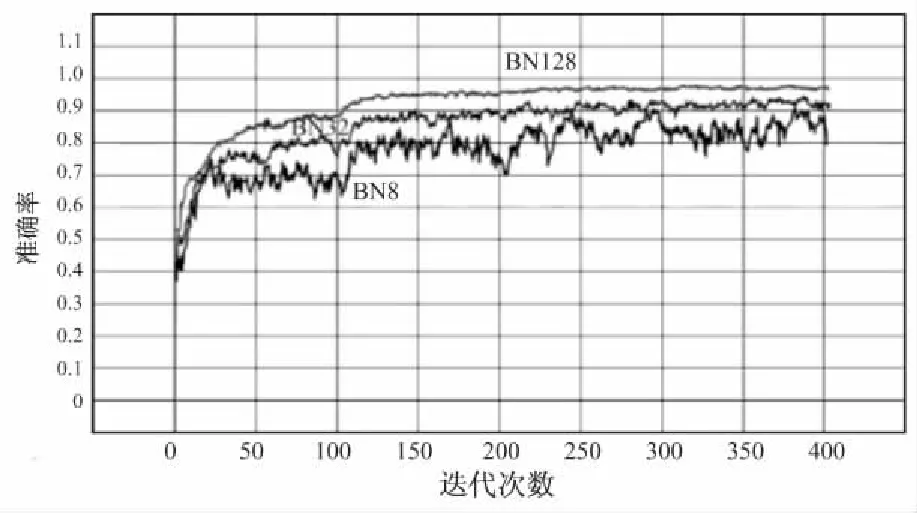
如图4所示,卷积核归一化在训练中准确率收敛较快,最后达到的准确率与批量归一化基本一致。
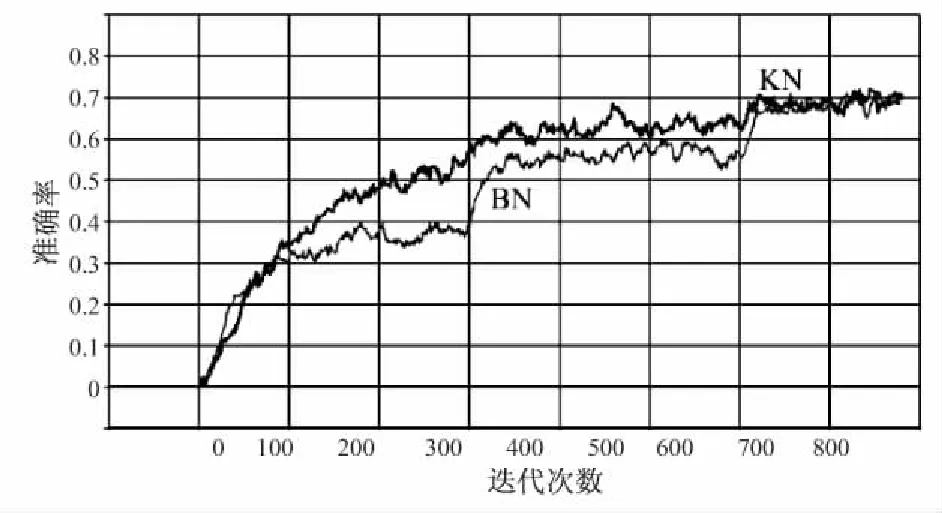
图4 ImageNet+ ResNet50训练准确率与迭代次数的关系
ResNet50的ImageNet测试集准确率如表6所示,准确率误差不超过0.5%。
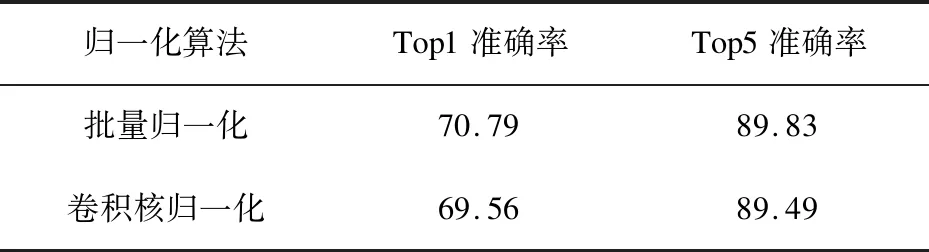
表6 ImageNet+ResNet50测试集准确率 %
4 结束语
文中提出了一种卷积核归一化算法,有效减少了特征间的内部协方差位移,加快了网络模型的训练速度。卷积核归一化算法在达到与批量归一化算法相同效果的同时(准确率误差不超过1%),有效解决了在批过小时批量归一化存在的问题,并且比批量归一化算法减少了75%至81%的计算量。
目前仅考虑了卷积核归一化算法在图像分类、目标识别等使用卷积神经网络的应用,接下来将进一步考虑将卷积核归一化算法应用到语音识别、自然语言处理等循环神经网络中,扩大卷积核归一化算法的适用性,提高深度神经网络的训练速度,减少计算量和存储空间。
