基于多尺度空间相关的气象要素预测
2019-12-11刘丽丹
刘丽丹
(南京航空航天大学 计算机科学与技术学院,江苏 南京 210018)
0 引 言
空间相关,是指一些变量在同一个分布区内的观测数据之间潜在的相互依赖性。如果是同一个变量在不同空间位置的变化存在相互依赖关系,称为空间自相关,不同的变量之间的空间相关则为空间互相关。气象要素的空间自相关反映的是一个站点观测到的要素值与附近相邻站点的同一种要素值的相关程度,是一种检测与量化各站点间该要素的空间依赖性的空间统计方法。由于大气的连续性,气象要素的空间自相关性是比较明显的,比如相邻地区的海平面气压值,一般都是平稳变化的。但由于受观测站地形的影响,某些要素值的空间自相关性也会表现的不同,比如山顶和山脚两个测站的气温,有海拔高度的因素,也有日照的影响,单从水平空间距离考虑,空间相关性可能就不明显。
概率图模型是用图形来表达变量之间相关关系的概率模型,可以简洁地刻画出复杂分布的结构,具有表示、推理和学习的能力[1],现已被广泛应用于机器学习、计算机视觉、自然语言处理、语音识别、专家系统、用户推荐、社交网络挖掘、生物信息学等研究领域的最新成果中[2-3]。概率图模型可以根据边的性质分为两类:一类是使用有向无环图表示变量之间的依赖关系,称为有向图模型或贝叶斯网;另一类是使用无向图表示变量之间的相关关系,称为无向图模型或马尔可夫网[4]。目前,无向图模型的主要应用包括图像重构、图像分割、图像恢复、3D视觉、目标识别和目标匹配等[5]。高斯图模型是概率图模型的一种,是无向图模型,它假设变量服从高斯分布。高斯图模型虽带有强假设,但在数学上易于处理,而且根据中心极限定理,可以较好地近似实际连续分布[6],可用于异常目标检测[7]和图像分割[8-9]等领域。而条件高斯图模型,不仅能模拟随机变量之间的条件相关关系,也能模拟随机变量与协变量之间的条件相关关系。
对于条件高斯图模型来说,边的估计,即是估计其协方差矩阵,亦是估计其精度矩阵。对于精度矩阵的估计,比较常用的方法有Lasso、牛顿法、坐标下降和梯度下降等等。1996年Lauritzen等用greedy forward-backward search方法来估计精度矩阵[10],但被认为在计算上并不可行。Friedman等提出了Graphical Lasso算法,以L1正则项控制精度矩阵的稀疏度,用最大似然来估计精度矩阵[11]。后来又不断涌现出多种方法,比如:梯度下降算法[12]、平滑优化法[13]、块坐标下降法[14]、交替线性优化法[15]、二次逼近法[16]等等。Matt Wytock提出了一种二阶有效集的方法求解稀疏条件高斯图模型,通过迭代得到不带L1惩罚项的目标函数的二阶近似,然后求解一个L1正则化二次规划来找到牛顿步长的正则化模拟。这种方法在大规模问题中更加实用,速度也更快[17]。
由于天气系统的特征尺度不同,在不同的时间尺度上,所需的验证空间也是有区别的。如果要预测6小时后某一站点的气象要素,和它相关的或者说是能够影响预测结果的站点,与该站点的空间距离应被限定在一个较小的范围,而如果预测时效为7天,则空间相关的距离就应该相应扩大。当然天气或要素的模拟推断并非如此简单,还有天气系统间的相互作用必须要考虑,在各种尝试之后,根据预测时效来调整空间距离影响的权重,在模型初始化阶段引入相似度矩阵,建立多尺度空间相关模型(MS-CGGM)。一方面能够提高模型计算效率,另一方面也可以达到去噪效果,提高预测精度。
1 多尺度空间相关图模型
设输出变量为Y∈Rn×p,输入变量为X∈Rn×q,q=m×p,n为样本量,p为站点数,m为协变量维数,即参与预测的气象要素个数。利用条件高斯图模型,有:
Y=f(X)=-C-1Θ-1X
(1)
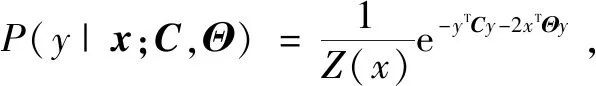
样本对{yi,xi}i∈n的对数似然为:
(2)
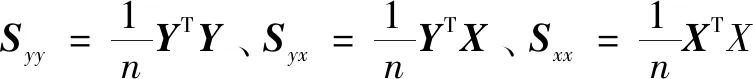
应用Matt Wytock的估计方法[17],最小化负对数似然并加入1惩罚项,即:
(3)
根据一阶非光滑优化方法,f(C,Θ)的梯度定义为:
(4)
在每次迭代中使用有效集方法,如果
(5)
每次只优化一个(ΔC)i,j或者(ΔΘ)i,j。
由式6得到牛顿加速方向:
(6)
二阶有效集方法地流程如下:
(1)给定X,Y,λ,初始化C=I,Θ=0;
(2)用式5计算有效集SC、SΘ。
(3)根据式6寻找牛顿加速方向DC、DΘ;
(4)用回溯线搜索法(backtracking line search)计算步长α(期间要保证C是正定的);
(5)迭代:C←C+αDC,Θ←Θ+αDΘ;
(6)返回步骤2。
由此得到C和Θ,C即为空间相关关系矩阵。
根据如上所述,引入一个相似度矩阵D,根据天气的特征尺度对预测模型施加约束。

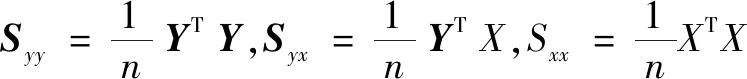
式2转换为:
(7)
再应用二阶有效集的方法估计C和Θ,得到空间相关关系矩阵。
2 实验与结果
2.1 实验数据与评估标准
采用全球国际交换站2003—2012共10年的定时气象观测数据,来源于全球地面天气资料定时值数据集。由于一些站点数据不全,经过筛选,选取了遍布全球各个州的3 431个站点,将数据进行了清理、归一化和中心化,以前9年数据为训练数据集,2012年数据作为测试数据集。
2.2 实验结果
为了学习全球范围的观测站点之间的空间相关关系,尝试了不同的方法。空间范围大至全球后,简单的条件高斯图模型处理起来有些困难,迭代次数明显增多,学习出的空间关系参考价值也不明显。图1为第1—50号站点的空间相关系数图,其中各图按预测时效区分,图a是6小时,图b是24小时,图c是72小时,图d是7天。图中坐标示数代表站点。
如果直接使用天气系统的特征尺度设定一个空间相关边界,效果也不理想,预测误差明显变大。图2是人为设定相关边界的空间相关系数图,左图为24小时降水空间相关关系数,右图为6小时气温空间相关关系数图,图中坐标示数代表站点。这种强假设带来了相关关系数图中过于清晰的边界,忽略了天气系统之间的相互作用,并且到底哪种距离范围更合适也很难界定,所以此种方法并不可取。
应用多尺度空间相关模型,先用交叉验证法根据预测时效选择代表带宽的参数b,选择使得误差最小的带宽,得到表1所示的时间-空间尺度约束。
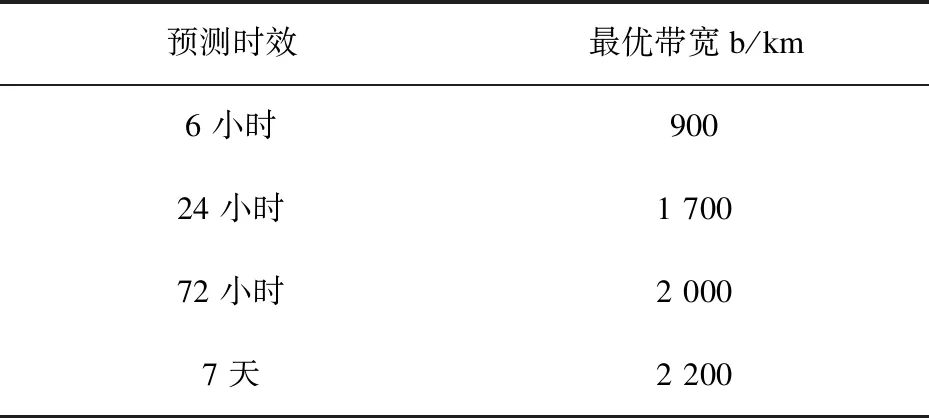
表1 不同预测时效对应的最优核函数带宽

图1 CGGM得到的1-50号站点不同时效空间相关系数图
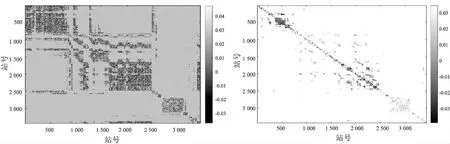
图2 带相关边界约束的空间相关系数图
利用多尺度条件高斯图模型对全球3 431个站点进行训练,得到了不同预测时效下的空间相关关系。图3是第1—50号站点的空间相关系数图,其中各图仍然按预测时效区分,图a是6小时,图b是24小时,图c是72小时,图d是7天。图中坐标示数代表站点。

图3 MS-CGGM得到的1-50号站点不同时效空间相关系数图
由图3可见,相比于图1,站点间的空间相关关系更加简洁清楚,对于空间距离权重也有所反映,但不像图2那样有强假设的边界。从预测准确率来看,此方法也较前两种更优,见表2。在模型预测效果评估中,采用检验回归模型较普遍的两个评价指标:均方根误差(RMSE)和绝对误差(MAE),具体表达式为:


表2 几种条件高斯图模型预测性能对比
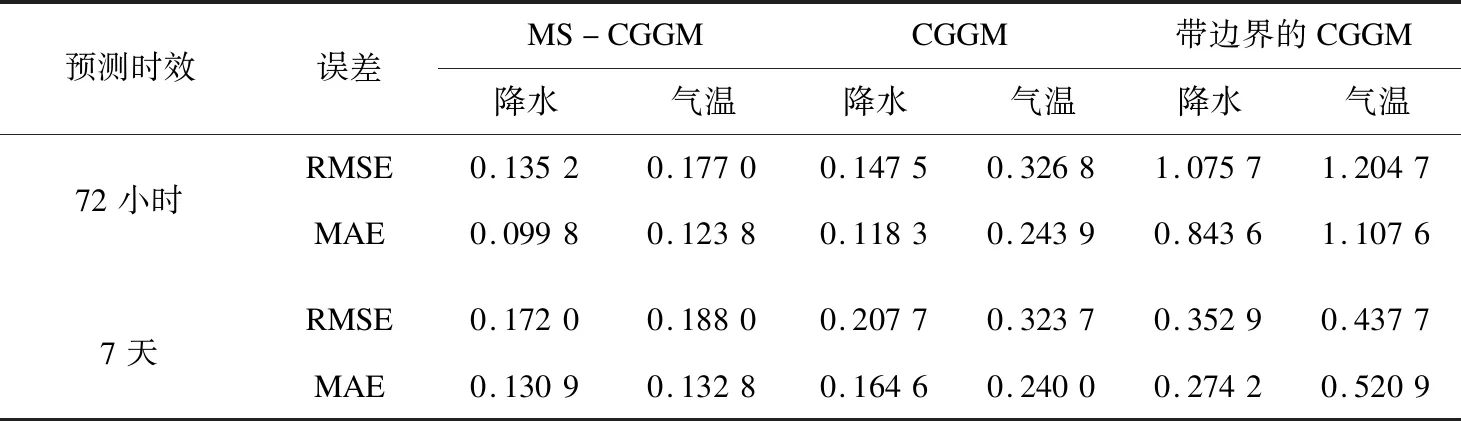
续表2
并且,多尺度条件高斯图模型的运行效率有明显提升,初始条件的改善使得收敛速度更快,迭代次数由平均496次减少到平均321次,运行时间明显变短。
3 结束语
根据预测时效的不同,提出了多尺度空间相关模型,在条件高斯图模型的基础上进行改进,引入相似度矩阵,对协方差矩阵进行迭代前的先验约束,减少迭代次数,提高效率。实验结果表明,多尺度空间相关模型能够快速学习全球气象观测站的空间相关性,空间相关根据预测时效不同而表现出差异,预测效率和准确率都有所提升。
