将“探究”进行到“底”

谈梅

《多边形内角和》是一次探索规律的活动。本课的教学目标是使学生通过观察、操作、归纳、类比等具体活动，探索并发现多边形的内角和与边数之间的关系，并用自己能理解的方式表示所发现的规律，积累一些探索数学规律的经验。之前听过其他老师的这节公开课，课堂上教师好似“设计师”，学生看似在探究，实则只是“操作工”。笔者认为在探究过程中学生真实的体验、感悟及积累的经验应该是教师关注的重点。带着疑惑，带着思考，在市级联片教研活動中，笔者选择了这节课，和教师们共同研讨。

一、课前思考

如何让学生真正经历探究，获得探索规律的经验。教学前我作了几点思考：

1.创设生活情境，激发学生探究动机

本课开始我设计由水立方墙面上的图形引入，使学生真实而强烈地感受数学就在身边，用数学的实际意义和应用来引发学生对数学的热爱之情。创造这样的生活情境可以激发学生的好奇心和创造力。

2.精心设计问题，引领学生自主思维

小学生的探究欲望往往是在课堂中被问题所激发，课中我准备了几个核心性、挑战性、综合性的问题。这些问题抓住数学学习的本质，让学生体会到数学学习不仅要知其然，更要知其所以然。

3.营造和谐氛围，鼓励学生质疑

学会学习的一个重要环节是学会质疑，问题可以是自己的疑惑、困难，也可以是自己的发现等等。本课学习中我将鼓励大家大胆猜想、质疑。

4.解放手、口、脑，积累探究经验

“儿童的智慧在自己的指尖”现代教学论认为探索能力和创新意识不是靠教师教出来的，而是“做出来的”。在多边形内角和的探究上我将让学生充分体验、感受、探讨，让学生实实在在地参与探究过程。

二、课堂实践

1.创设情境，激起欲望

师：同学们，知道这是什么地方吗？（出示图片，   ）

师（激动）：对，这里就是2008北京奥运会的主游泳馆水立方。仔细看，在这个宏伟的建筑物的墙面上你都看到了什么？

生答，师贴图形。

师：像这样的一些图形在数学上统称为多边形。这节课我们一同来走进多边形的世界......

（设计意图：从水立方墙面图形引入，学生自豪感油然而生，同时切实感受到多边形的价值，为后续学习打下了良好的基础。）

2.探究一：四边形的内角和

师：关于多边形你有哪些了解？生答。

师：在多边形王国里，你知道谁是最简单的多边形吗？生答。

师：没错！有关三角形，你有哪些了解？

生答，师贴：内角和、180°。

师：那么四边形、五边形、六边形......呢？你猜它们的内角和会是怎样的？

生：我猜四边形的内角和也是一个固定的数量。

生：我觉得边数越多，内角和越大。

师（疑惑）：猜的对不对呢？大家能不能自己想办法来解决？先研究哪个呢？

生：四边形，因为它最简单。

师：有道理！从简单问题入手。（贴：简单）

出示要求：（1）独立思考，尝试找到方便、快捷的方法。（2）完成后四人小组交流。

生：我量出每个角的度数，算出和是360°

生：我剪下四个角，拼出360°

生：我将四边形分成了两个三角形。

师：别急，老师借你笔，现在你可是小老师，争取让每一位同学都能听懂你的想法！

生（提高了音量）：我把四边形分成了两个三角形，这个三角形的内角和是180度（教师及时提醒学生用红色水彩笔标注三个角），另一个三角形也是180°（提醒学生用蓝笔标注三个角），180°+180°=360°。

师： 倾听真的是一种好的学习习惯。你们看，这三个红色的角和三个蓝色的角合起来就是......

生（齐答）：四边形的内角和

板书：180°×2=360°

师：刚才大家用了量、拼、分的方法找到四边形的内角和，你更喜欢哪一种方法？（学生说出量、剪方法的弊端）

师：老师特别赞同你们的意思，解决问题时我们就要有这种选择较方便方法的意识，将研究的新问题转化为求两个三角形的内角和来解决。（贴：转化）

（设计意图：先让学生大胆猜测多边形的内角和，然后鼓励学生自己想办法验证猜想。整个过程由学生主导，学生尝试着各种方法解决问题，乐此不彼。）

3.探究二：五边形、六边形的内角和

师：接下来你想研究几边形呢？

生：五边形。

生：我觉得都可以，不管哪一个我把它分成三角形就行了。

师：是这样吗？（出示五、六边形）带着你刚才的解题经验开始吧！

学生介绍五边形的内角和，中途教师提示学生用不同颜色的水彩笔标注。

师小结：这3个三角形的内角和恰好就是......

生（异口同声）：五边形的内角和。

生：老师，我把它分成了三角形和四边形，可以吗？

师：当然！敢于提出不同的看法，真棒！

学生上台介绍六边形的内角和。

生：我把它分成四个三角形。

生：我直接分成了两个四边形。

生：还可以分成两个三角形和一个四边形。

师：同学们，你们让老师大开眼界啊，老师把这个大大的赞送给你们（竖起大拇指），瞧，老师还看到一种分法（展示从同一个点和不从同一个点出发的分法），比较一下，你更喜欢哪一种？生答。

师小结：看来分也有窍门，从同一个点出发的分法更清楚有序。

（设计意图：教师在这个教学环节让学生充分体验、大胆尝试。通过这样的教学，学生对知识的理解，学习方法的掌握会更深刻。）

4.探究三：发现规律

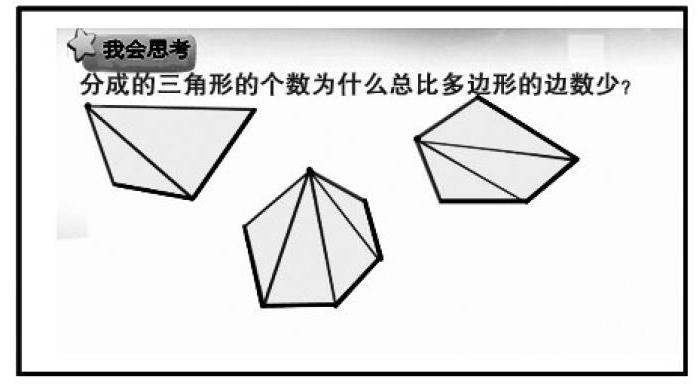
师：仔细观察图形你发现了什么？

生：我发现分成的三角形的个数总比多边形的边数少2。

生：其实算多边形的内角和只要把180°乘三角形的个数。

师：这些发现，在其它多边形身上还适用吗？这需要我们进一步举例验证（出示七、八、九、十边形）。

出示要求：1、四人小组合作，每人研究一个。2、完成学习单后思考：之前的发现还适用吗？

小组汇报。

师：之前的发现在这几个多边形中还成立吗？

生（点头）：成立！

师：如果继续研究下去还会成立吗？

生（坚定）：成立！

师：那就是说这是一条不变的规律。

出示：十二边形，它的内角和多少呢？快速汇报。

师：任意一个多边形呢？学生口头汇报。

师：谁能用一个式子来概括多边形内角和的计算公式？

生答后板书公式。

师：边数-2算的是......生答。

师（疑惑）：咦！为什么分成的三角形的个数总比多边形的边数少2呢？

播放课件，鼓励学生对照课件上台讲解。

师：在数学学习中我们不仅要

知其然，更要知其所以然。问题解决了，我觉得我们还得回头来看一看我们的学习过程，我们是怎样做的呢？

生：我們把复杂的新问题转化成了原来学过的知识。

生：得从简单的问题入手，向复杂问题研究，进行有序思考。

师：同学们真厉害，不仅会学习还会反思！

（出示书）认识书上的这个老爷爷吗？ 他可

是古希腊著名的数学家欧几里得。 看，书上这

里的n指什么？（生答）竟然和你们发现的规律一样，看来你们也有数学家的头脑，真为你们感到骄傲！期待未来你们也能成为数学小巨人！

（设计意图：“为什么分成的三角形的个数比多边形的边数少2”问题虽比较难，但课件的配合巧妙地解决了这一难题。之后引导学生“谈体会”，帮助学生整理探索过程中积累起来的经验，感悟类比、归纳、转化等思想方法。）

三、课后反思

纵观整个课的教学设计和组织实施，充分体现“以学生发展为本”教育理念，初步建构探究型的课堂教学模式。

本课的成功之处：

（1）营造宽松和谐的氛围，给探究提供保障。课堂中教师对学生积极的鼓励，友好的眼神，期待的目光，关切的手势和充满爱意的微笑，都给予学生情感的支持。

（2）提出的问题具有启发性，抓住探究的核心。如：1.为什么分成的三角形的个数总比多边形的边数少2？2.在探寻规律的过程中，你又有哪些经验要与同学分享的呢.....这些问题是这节课的核心问题，构成本节课的教学主线。

（3）教师适时点拨，帮助学生领悟探究方法。如：1.老师特别赞同你们的意思，解决问题时我们就要有这种选择较方便方法的意识。2.师：看来分也有窍门，从同一个点出发的分法更清楚有序。这些小结语既能激励学生，又能让学生从中感悟基本的数学思想方法。

（4）提供自我探索、自我思考、自我创造的实践机会。教学中有时“放手”会带来惊喜，其实让学生“动起来”实质上是在关注学生的思考，关注学生的学习状态，关注学生的学习情感。这样的数学课堂自然就会呈现与众不同的精彩！

简而言之，在数学课堂上，公式、概念、方法并不是最重要的，教学该赋予数学课更丰厚的意义—就是真实的体验、创造的激情、探究的能力。