多进化策略自适应免疫多目标进化算法

康 锰,许 峰

(安徽理工大学数学与大数据学院,安徽 淮南 232001)

根据待优化目标函数的数量，科研和工程应用中广泛存在的优化问题可分为单目标优化问题和多目标优化问题(Multi-objective Optimization Problem， MOP)。由于多个目标间往往是相互冲突的，所以多目标优化算法通常提供的是一组能平衡各目标的均衡解，即Pareto最优解集(Pareto Optimum Solution Set， PS)，目标函数在PS上值的集合称为Pareto最优前沿(Pareto Optimum Front， PF)。多目标优化要求算法的解既要尽可能地逼近真实的PF，又要沿着真实PF尽可能地均匀分布，即Pareto最优解集的收敛性和分布性。由于进化算法基于种群的特性，多目标进化算法(Multi-objective Evolutionary Algorithm， MOEA)被公认为求解MOP最有效的方法。

优化中著名的“No free lunch”定理表明，没有一种优化方法对所有问题都是有效的，各种方法都有其相应的优势和劣势。对于某些复杂的优化问题，单一的优化方法很难获得令人满意的解。因此，将不同优化算法混合，通过交叉、融合产生新算法是智能优化算法的一种重要研究思路。免疫多目标进化算法正是将人工免疫系统引入多目标进化算法而产生的新型多目标进化算法。

大多数免疫多目标进化算法均采用克隆选择，其优点是收敛速度较快，但过强的选择压力也使得这种选择方法在一定程度上降低了种群的多样性，容易导致算法陷入局部收敛。2002年，文献[1]最先注意到了基于克隆选择的免疫多目标进化算法的这个缺陷;2003年，文献[2]提出了一种平衡收敛速度和种群多样性的思路。近年来，利用混合的思路改善免疫多目标进化算法的工作取得了不少进展[3-4]。2009年，文献[5]将差分进化策略引入免疫多目标进化算法;2015年，文献[6]提出了一种基于克隆选择和差分进化的免疫多目标进化算法;2016和2017年，文献[7-8]分别给出了一种在免疫多目标进化算法中进行自适应选择参数和自适应选择进化策略的方法。

文献[9]最早在量子遗传算法中用目标函数的梯度确定量子旋转门的转角，文献[10]42将目标函数的变化率用于自适应调用蚁群和遗传算法。本文将目标函数变化率引入基于克隆选择的免疫多目标差分进化算法，用以进行两种差分进化策略的自适应选择，利用DTLZ测试函数对新算法进行了数值实验和性能测试，并与其他算法进行了比较，验证了新算法的有效性。

1 克隆选择多目标进化算法

1.1 多目标差分进化算法

差分进化算法[11](Differential Evolution Algorithm， DE)是1995年Rainer Storn和Kenneth Price提出的一种基于进化思想和种群差异的群智能优化算法。DE算法的原理简单，受控参数少，全局收敛速度快。

多目标差分进化算法(Multi-objective Differential Evolution Algorithm， MODE)是在差分进化算法的基础上发展起来的一种多目标进化算法。本文采用的是基于克隆选择的多目标差分进化算法。

1.2 克隆选择

最典型的人工免疫算法是克隆选择算法。著名免疫学家Burnet于1958年提出了生物克隆免疫学说，其核心思想是：抗原有选择性地与相应的抗体进行反应。文献[12]根据Burnet的抗体克隆选择学说，提出了一种通用的克隆选择算法，流程图如图1所示。

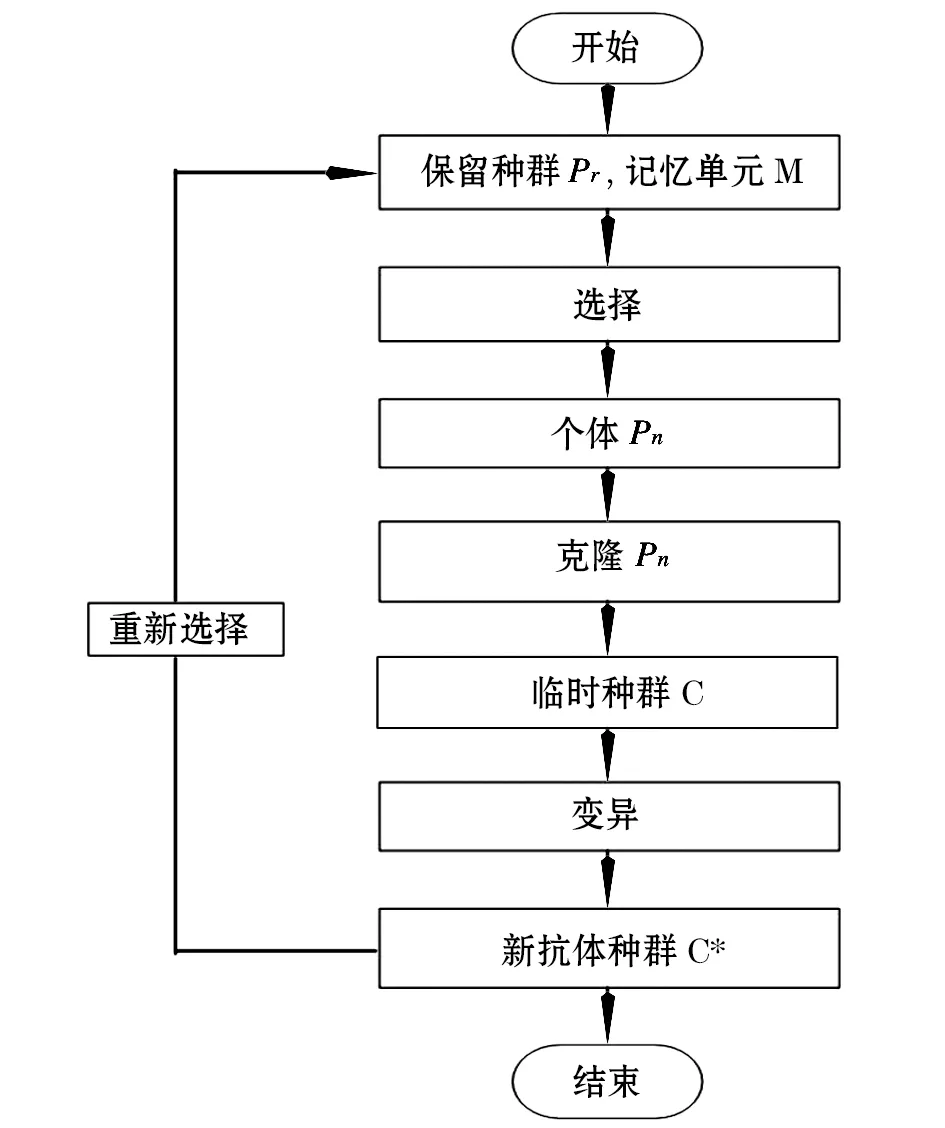
图1 通用克隆选择算法流程图

1.3 最优解集的评价标准

通常， 可以对多目标优化最优解集从解的收敛性和分布性两方面进行评价， 常用的量化评价指标[10]43有：

1) 收敛性指标γ

γ指标衡量非支配解集Q对理论Pareto最优解集P*的逼近程度，计算公式为

(1)

式中：di为非支配解集Q中的个体i与P*中距离最近个体的距离。显然，γ越小，表明算法取得的非支配解集Q逼近理论Pareto最优解集P*的程度越高，即算法的收敛性越好。

2) 分布性指标Δ

Δ指标衡量非支配解集Q中个体的分布性和均匀性，计算公式为

(2)

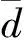
2 多进化策略多目标进化算法

2.1 两种差分进化策略

差分进化策略已被证明是多目标优化算法中的一种简单、有效的进化方法[13]3。在DE中，设置不同的控制参数可以使得DE呈现不同的搜索特性。本文采用下列两种DE策略[8]52：

DE1：Ui，j={Xr1，j+F·(Xr2，j-Xr3，j)+F·(Xr4，j-

Xr5，j)，r

(3)

DE2：Ui，j={Xr1，j+F·(Xr1，j-Xr2，j)，

r

(4)

式中：Ui，j称为试验向量，Xi，j是当前种群中的目标向量，F是比例因子，Cr是交叉率，r是[0，1]中的随机数，下标r1～r5是从[1，2，…，n]中随机选择的整数，下标j表示第j个决策变量。大量实验显示[13]31，F，Cr的取值范围应为：F∈(0.3，0.9)，Cr∈(0.1，0.9)。本文中，DE1中的参数为：F=0.7，Cr=0.4;DE2中的参数为：F=0.3，Cr=0.7。

F的值决定了搜索步长即搜索速度，F越大(小)，搜索步长越大(小)，搜索速度越快(慢)。Cr的值决定了子代(试验向量)可以从其父代(目标向量)中继承信息量的多少，Cr越小(大)，子代从父代中继承的信息量越多(少)。因此，相比较而言，DE1侧重于开拓新的搜索区域且搜索速度较快，即具有较强的全局搜索能力，而DE2则较容易生成新的个体，即有助于维持种群的多样性。

2.2 基于目标函数变化率的进化策略自适应选择方法

在进化早期，通常采用DE1以加快搜索进度，而在进化后期，则采用DE2以维持种群多样性，避免算法陷入局部最优。如何合理地动态调用不同的进化策略是进化计算中一个值得研究的问题。

考虑到在进化早期，目标函数的变化率较大，而在进化后期，目标函数的变化率则较小，本文采用下列方法自适应地动态调用DE1和DE2[10]44。

定义

(5)

其中

(6)

(7)

对于离散优化问题，f(X)不存在梯度，则

(8)

(9)

(10)

其中，Xp，Xc分别表示父代和子代个体。

当γij小于设定的阈值ε(通常取为10-2)时，选择DE1，否则选择DE2。

2.3 算法流程

本文提出的多进化策略自适应免疫多目标进化算法(Adaptive Immune Multi-objective Evolutionary Algorithm with Multi-evolutionary Strategy， AIMOEA)的流程如下：

Step1 种群初始化;

Step2 根据1.2中的算法对种群进行克隆选择;

Step3 对选择后的种群，根据2.2中的方法，选择DE1或DE2进行进化，生成新种群;

Step4 对新种群进行非支配排序，生成非支配集;

Step5 选择非支配等级低且拥挤密度小的个体作为精英个体，构成下一代进化种群;

Step6 若满足终止条件，则算法终止;否则转Step2，直至满足终止条件。

上述算法中之所以采用了精英选择，主要目的是防止在优化过程中由于随机因素和群体规模的限制而丢失优良解。

3 数值实验与算法性能评测

为了评测AIMOEA算法的性能，选取DTLZ6和DTLZ1两个测试函数进行数值实验。选用这两个测试函数的原因是前者的PF为空间曲线，而后者的PF为空间曲面。硬件配置为Intel Core I5 2.5GHz、4G内存，开发环境为Matlab2014。实验参数设置：进化代数为100，种群规模为100，交叉概率为0.8。

图2～图7分别给出了AIMOEA、NSGA-II和MOEA/D-DE三种算法生成的DTLZ6和DTLZ1的最优前沿。选择NSGA-II和MOEA/D-DE作为对比算法是由于NSGA-II是经典的第二代多目标进化算法，MOEA/D-DE[8]61则是收敛性和分布性较为均衡的多目标进化算法。

图2 DTLZ6的AIMOEA算法最优前沿

图3 DTLZ1的AIMOEA算法最优前沿

图4 DTLZ6的NSGA-II算法最优前沿

图5 DTLZ1的NSGA-II算法最优前沿

图6 DTLZ6的MOEA/D-DE算法最优前沿

图7 DTLZ1的MOEA/D-DE算法最优前沿

从上述图形中可以直观地看出，AIMOEA算法得到的Pareto最优前沿较好地逼近了理论Pareto最优前沿，而且具有较好的分布性和均匀性。

为了进一步定量地评价AIMOEA算法的性能，本文将其与NSGA-II和MOGA/D-DE对DTLZ6和DTLZ1的优化情况进行了比较，评价标准采用通用的γ指标和Δ指标。对比实验中的参数均采用相应文献中的推荐值，γ指标和Δ指标为各算法独立运行20次的平均值，具体结果见表1。

表1 三种算法的γ和Δ指标对比

表1中的γ指标和Δ指标表明，AIMOEA算法在解集的收敛性和分布性两方面均在一定程度上优于NSGA-II;与MOEA/D-DE相比，AIMOEA算法在解集的收敛性上稍逊一筹，但在分布性方面则占有一定优势。在一定程度上说明，AIMOEA算法中的克隆选择可以保证算法的收敛性，而自适应动态调用两种不同的差分进化策略的确可以改善种群的多样性，从而提高解集的分布性和均匀性。MOEA/D-DE算法收敛性较好的原因是其在MOEA/D算法的基础上也加入了差分进化策略。

4 结论

数值实验结果和统计指标显示，本文提出的多进化策略自适应免疫多目标进化算法可以根据目标函数变化率动态地选择不同的差分进化策略，在保持克隆免疫算法收敛速度高的同时，所得的解比单进化策略算法的解具有更好的分布性和均匀性。虽然大多数学者都认为人工免疫系统可以有效地克服进化算法中早熟和种群多样性下降等缺陷，但至今没有理论上的结果，对算法性能的研究只能局限于对测试函数的对比实验，在一定程度上影响了进化算法的研究和应用价值。另外，实验表明，参数F，Cr的取值对算法的收敛性和解的分布性、均匀性有一定影响。因此，如何选择、优化参数F，Cr是今后值得研究的问题。