基于AO*算法的舰炮制导弹药多故障诊断策略设计
2019-12-10孙世岩张弘弨
陈 锋,严 平,孙世岩,张弘弨
(1.海军研究院,北京 100161;2.海军工程大学,湖北 武汉 430033)
测试的最终目的是隔离故障,而在系统执行测试的过程中,可能根据得到的部分测试结果已经能够隔离故障源,此时系统不必再进行其他的测试操作。而诊断策略的设计,会大大影响测试成本以及故障隔离速度。诊断策略设计工作主要包括:建立故障-测试相关性模型;建立相关性矩阵;优选测试点以及设计诊断策略[1-2]。
本文在优选测试点的基础上,采用与或图启发式搜索算法设计了舰炮制导弹药多故障诊断策略,降低了舰炮制导弹药测试成本并提高了故障隔离速度。
1 舰炮制导弹药多故障问题描述
诊断策略设计的研究一般建立在单故障,即假设系统某一时间只发生一个故障的前提下,但像舰炮制导弹药这样的复杂系统,这种假设显然是不成立的。单纯地按照单故障的诊断策略下结论,很可能因为存在隐含故障和伪故障而出现误诊或漏诊的情况[3]。因此,研究多故障问题的诊断策略的第一步就是识别系统可能存在的隐含故障和伪故障。
1)隐含故障:系统发生多个故障时,系统总体表现的故障特征与其中某一故障的故障特征相同,即系统总的故障特征隐藏了其中一个故障的故障特征。存在隐含故障很容易使故障诊断出现漏诊的情况。
2)伪故障:系统发生多个故障时,系统总体表现的故障特征与发生故障之外的某一故障的故障特征相同,系统总的故障特征与某个不相关单元的故障特征相同。存在伪故障很容易使故障诊断出现误诊的情况。
由相关性分析理论可知,fi的故障特征可用集合FS(fi)={ti|aij=1,tj∈T}来描述,同理,fi和fj同时发生的故障特征可用FS(fi,fj)来描述,则有FS(fi,fj)=FS(fi)∪FS(fj)。若存在FS(A)=FS(A)∪FS(B)=FS(AB),则存在隐含故障,且故障B为故障A的隐含故障;若FS(C)=FS(A)∪FS(B)=FS(AB),则存在伪故障,且故障组合{A,B}为故障C的一个伪故障[4]。
2 AO*算法求解诊断策略优化问题
测试性分析中所采取的检测手段均为二值测试,也就是说每项检测的结论只有通过和不通过两种,所以可由执行测试的顺序以二叉树形式画出系统的故障诊断树,即测试序列等价于故障诊断树。基于这样的关系,诊断策略即测试序列的优化设计过程也就等同于生成系统的故障树的过程。而故障树又和与或图在形式上非常相近,因此可视故障诊断树为一类广义上的与或图。因此本文选用启发式搜索算法,通过求解与或图得到优化的测试序列[5-6]。
2.1 AO*算法求解单故障诊断策略
AO*算法是一种启发式搜索算法,该算法的评估函数为霍夫曼编码平均字长。霍夫曼编码的编码字长不同,编码时通过尽可能使故障概率越大的事件字长越短,使编码的效率变高。其编码步骤是,首先,由小到大依次排列故障概率,再将最小的两个概率相加,并用得到的概率和将其替换,再将全部故障概率进行排列。如此循环,直到得到整个霍夫曼树。过程中通常将两个最小概率中相对较小的故障以0编码,而相对较大的以1编码。循环结束后,所有故障均与一串二进制编码一一对应,加和每个故障概率与其码长的乘积,再除以全部概率的总和,计算结果就是平均霍夫曼编码字长。解决故障诊断问题时上述过程可表示为

(1)
其中,w*(x)为故障集的霍夫曼编码平均字长,w*(fi)故障fi的霍夫曼编码字长,且fi∈x。
评估函数(HEF)通过故障诊断树和霍夫曼树的等价性来确定。为说明该过程,举一个普适性例子,假设测试成本大小顺序为0≤c1≤c2≤…≤cn,HEF(x)最小值为

(2)
其中,w′(x)=[w*(x)],为对模糊故障集X的霍夫曼编码平均字长取整。
上式即为算法的启发式评估函数,从总的故障集开始向下搜索,当所有故障均被搜索到时,由公式(3)计算实际的测试成本,由公式(4)修正测试成本,由下至上进行回溯,直至回溯到根节点。

(3)
e=min(Exi)
(4)
其中,Exi为对模糊故障集X执行测试ti时的实际成本,xip、xif分别是对模糊故障集X执行测试ti时通过和不通过的子集,ci为ti测试成本,P(xip)、P(xif)分别为xip、xif的概率和;E(xip)、E(xif)分别为xip、xif实际的测试成本。
只考虑单故障时,算法步骤主要有以下两个方面:由上至下进行评估和由下至上进行修正,具体步骤为:
1)判断故障集F中元素是否超过两个,当元素超过两个时继续进行以下步骤,否则转到步骤7);
2)对故障集F,按照故障-测试相关矩阵中测试与故障的关系以及每个故障发生的概率分别对每个测试进行霍夫曼编码,进而评估其测试成本:
e=min{ci+HEFxip×P(xip)+HEFxif×P(xif)}
(5)
3)比较所有测试的测试成本评估值,标记最小评估值相应的测试编号,以及该测试的父节点和左右子节点;
4)以左子节点中的模糊故障作为新的故障集合F,重复步骤1)到7),计算左子节点测试的实际成本;
5)以右子节点中的模糊故障作为新的故障集合F,重复步骤1)到7),计算右子节点测试的实际成本;
6)比较左右节点测试的实际成本和记录的测试评估成本。若实际成本大于评估值,则修正评估值并删除该路径,选择测试评估成本次小的对应的测试,返回步骤3),否则继续向下执行;
7)继续向上修正评估代价;
8)重复步骤1)到7),直至故障集合F中元素个数不大于2时,测试选择的测试序列的实际成本最低,得到最优故障诊断树,算法结束。
2.2 AO*算法求解多故障诊断策略
多故障的诊断策略在单故障的设计方法上进行了扩展。其步骤如下:
1)采用上述方法构造一个单故障诊断树。
2)判断故障诊断树所能隔离的故障是否存在隐含故障或伪故障,若不存在,则维修该叶子节点所对应的故障,不再执行其他操作。
3)若存在隐含故障或伪故障,首先通过维修,排除该故障,再针对该故障的隐含故障集或伪故障集构造附加的诊断策略,直至确定系统不存在隐含故障和伪故障[7]。
3 舰炮制导弹药控制系统诊断策略设计
舰炮制导弹药控制系统多信号流图模型如图1所示。

图1 舰炮制导弹药控制系统多信号流图模型
省略优选测试点过程,经优选测试点后的舰炮制导弹药控制系统的相关矩阵如表1所示,故障源共13个,分别为卫星电平转换模块、卫星天线、卫星接收模块、卫星定位解算模块、DSP、地磁传感器电平转换模块、地磁传感器、DSP电平转换模块、舵机控制器电平转换模块、舵机驱动器、舵机驱动器电平转换模块、伺服电机、电源模块。故障状态共20个,其中G表示全局故障,F表示功能故障,优选测试点共12个。
3.1 单故障诊断策略设计
将无故障状态表示为f0,故障状态表示为{f1,f2,…f20}。假设12个测试的代价相等,均为1。无故障状态及20个故障状态的故障概率为
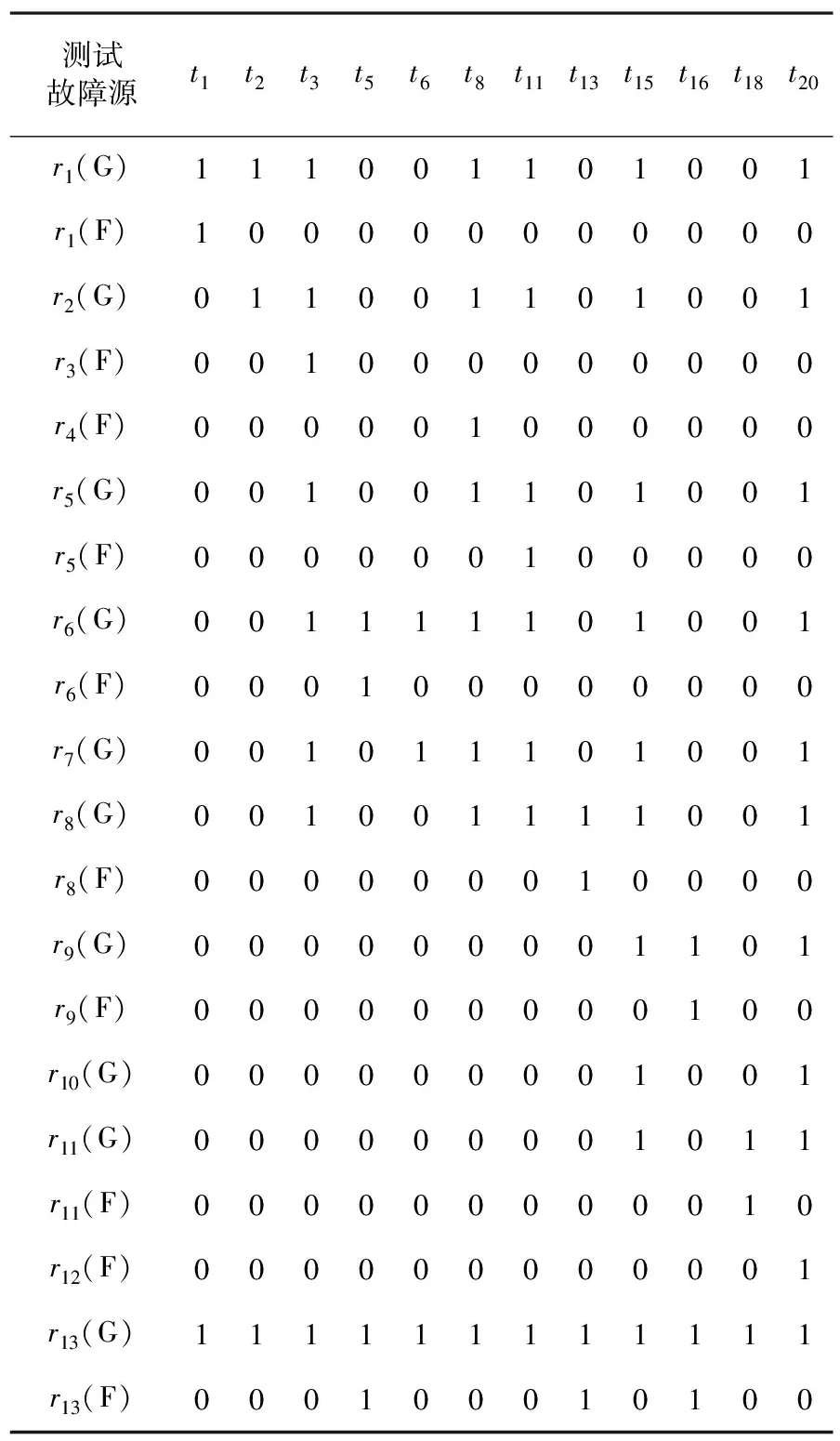
表1 遗传算法选择的测试集合
{0.5,0.02,0.01,0.1,0.02,0.03,0.01,0.01,0.02,0.03,0.01,0.01,0.02,0.03,0.02,0.05,0.01,0.02,0.05,0.02,0.01}。依照上文所述方法,由于故障状态较多,测试代价评估值计算量较大,为节省计算时间,本文通过Matlab编程求取每项测试的测试代价评估值,再结合AO*算法步骤求取舰炮制导弹药控制系统单故障诊断策略,得到的单故障诊断策略如图2所示。
分析图2可知,舰炮制导弹药控制系统内的所有故障都能够被正确检测和定位。经计算,测试代价为6.74,是原本测试代价12的56.2%。因此按照以上得到的诊断策略的顺序可以迅速隔离故障源,且所需的测试成本理论上是最优的。
3.2 多故障诊断策略设计
在得到单故障诊断策略的前提下,考虑多故障的情况,不限制并发故障数目,分析图2所示故障树中各叶子节点的隐含故障和伪故障,分析结果如表2所示。
根据多故障诊断策略设计方法,引入维修节点,得到的多故障诊断策略如图3所示。
3.3 故障诊断策略验证
若设置四个故障点,分别为f2、f4、f11和f15。故障表现如表3所示。

图2 舰炮制导弹药控制系统单故障诊断策略

表2 控制系统诊断树中各叶子节点隐含故障和伪故障分析结果
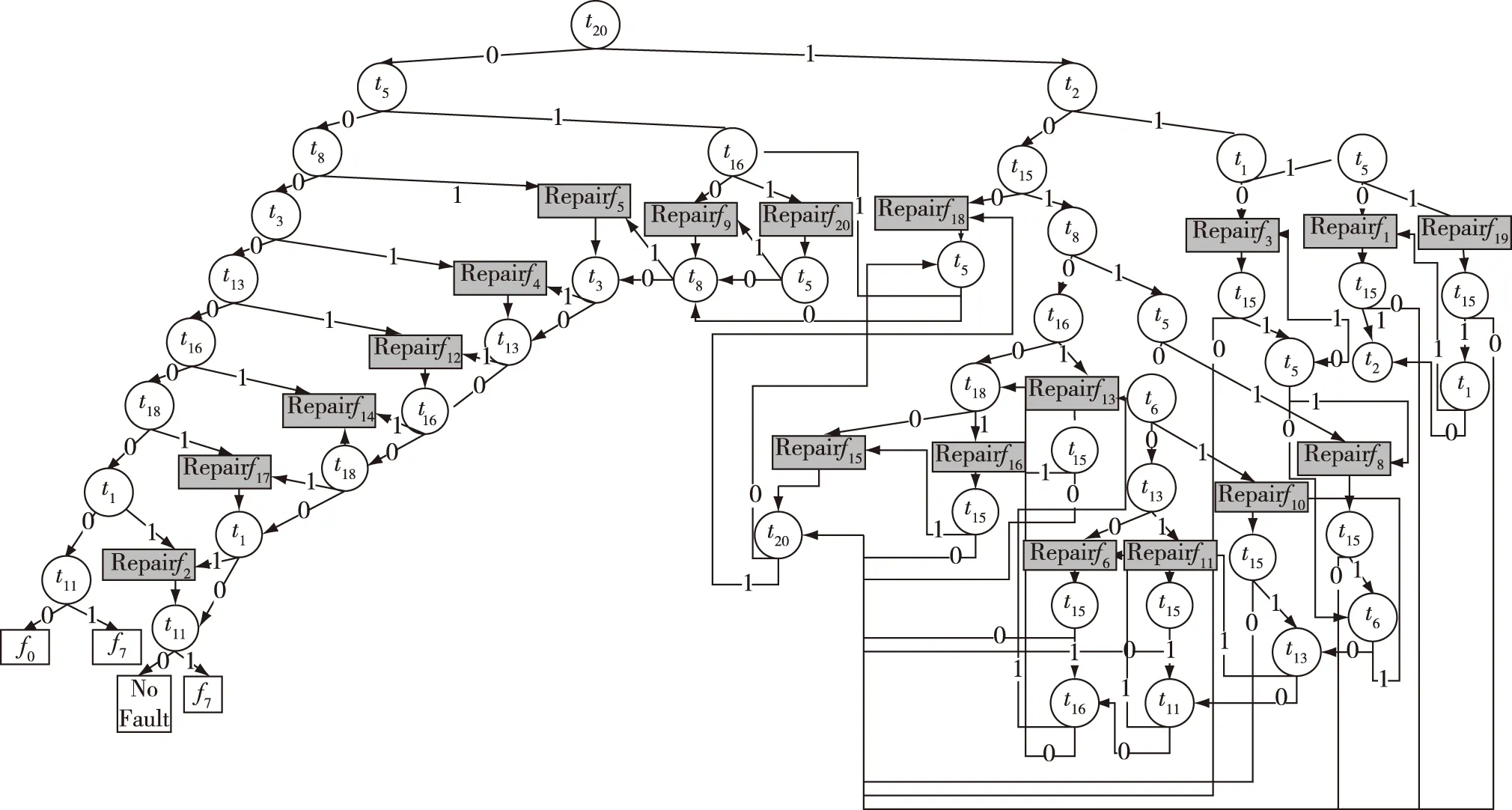
图3 舰炮制导弹药控制系统多故障诊断策略

表3 设置故障的故障表现
按照图3所示的诊断策略对故障进行诊断,诊断流程如图4所示。

图4 诊断流程
由图4可看出四个故障均被定位,则所有故障都可被排除,因此该故障诊断策略有效。
另设置三个故障点,分别为f5、f10和f16。故障表现如表4所示。

表4 故障表现
按照图3所示的诊断策略对故障进行诊断,诊断流程如图5所示。
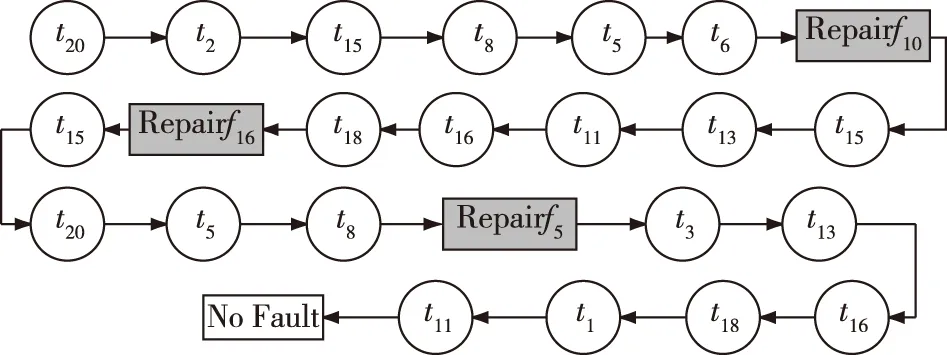
图5 诊断流程
由图5可看出,随机设置三个故障仍可以全部被定位,所有故障都可被排除,进一步验证了该诊断策略的有效性,可用于解决舰炮制导弹药多故障诊断问题。
4 结束语
本文提出了一种舰炮制导弹药多故障诊断策略的设计方法。该方法将AO*算法应用到解决舰炮制导弹药多故障诊断策略设计问题上,得到了舰炮制导弹药多故障诊断策略。通过验证表明,AO*算法对解决舰炮制导弹药多故障诊断策略问题有效,达到了降低舰炮制导弹药测试成本和提高故障隔离速度的目的。
