尺寸和加载速率对冻结水泥土单轴压缩影响

2019-12-09李东庆

水文地质工程地质 2019年6期

陈鑫，张泽，李东庆

(1.中国科学院西北生态环境资源研究院，冻土工程国家重点实验室，甘肃兰州 730000；2.中国科学院大学，北京 100049)

地层改良是人工地层冻结法中冻胀融沉防治的重要措施[1-2]，改良土在冻结法实施期间处于冻结状态。此外，地层改良广泛应用于季节冻土区和多年冻土区的路基工程和深基础工程中[3-4]。寒区地表都存在着一层冬冻夏融的冻结-融化层，改良土暴露于自然环境下，每年都有很长的时间处于冻结状态。为促进地层改良在控制冻胀融沉和寒区工程建设中的推广应用，就有必要深入系统研究冻结改良土的力学特性。

材料力学特性受材料自身和外部条件的影响，如温度、加载速率、冻融循环。已有关于改良土强度影响因素的研究主要集中在冻融循环、受力情况、温度及改良土自身特性方面(掺入比、期龄)。马巍等[3]对经历不同冻融循环次数的粉土和石灰改良粉土剪切强度的研究表明冻融作用强烈影响着改良土的剪切强度。王天亮等[4]考察了冻融次数、冷却温度和围压对水泥及石灰改良土静力特性的影响，认为反复冻融作用下水泥土的改良效果要优于石灰土。牛亚强等[5]通过常规三轴试验研究了围压对冻结改良黄土变形和强度的影响，认为改良后冻结黄土的强度得到明显的提高且水泥比石灰的改良效果更为显著。谭丽华[6]、储鹏[7]、王许诺等[8]通过室内单轴压缩试验研究了温度、水泥掺入比、期龄对改良土抗压强度的影响，研究结果均表明水泥土无侧限抗压强度随温度的降低、水泥掺入比的增加、养护龄期的增加而增大。此外，尺寸效应和加载速率也是影响岩土材料力学参数的重要因素[9-11]。杨圣奇等[9]研究结果表明试件尺寸对岩石强度和变形特性以及破裂形式均具有明显的影响，并基于试验结果提出了大理岩石材料尺寸效应的理论模型。已有研究[12-15]表明改良土和冻土的强度也受到试件形状和尺寸的影响，但目前仍未有文献就尺寸对冻结改良土强度的影响做出探讨。国内外学者关于加载速率对冻土强度和破坏特性的影响进行了大量的研究[16-20]。如比较常见的水泥改良土是一种准脆性材料，加载速率对其强度的影响是否同已有关于冻土的研究结果相同？因此，有必要研究尺寸效应和加载速率效应对冻结改良土力学特性的影响规律。

本文以水泥改良土为研究对象，开展不同尺寸与加载速率条件下冻结水泥土的单轴压缩试验，揭示了高径比和加载速率对试样强度与变形特性的影响规律。

1 试验概况

试验用土取自甘肃兰州市，取土深度为当地最大冻结深度以下1 m。基本物理性质指标为：塑限wP=15.6%，液限wL=27.7%，塑性指数IP=12.1，最优含水率为16.2%，最大干密度为1.74 g/cm3。土样的颗粒级配曲线如图1所示。从图1可以看出试验用土颗粒粒径主要分布在0.005～0.075 mm范围内，这就使得其通道连通性较好，毛细作用强，持水性好，为冻结过程中水分迁移提供了基本条件[21]。

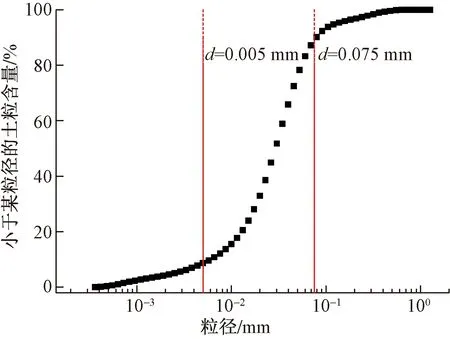
图1 试验土样颗粒级配曲线

1.1 试样制备

试验所用水泥为复合硅酸盐水泥P.C32.5。将试验所用土样风干、碾压、过2 mm筛，测定土样的初始含水率。试验设计水泥改良土中水泥掺量为15%，初始含水率为21.6%，干密度为1.7 g/cm3。制样时先根据水泥掺量计算出所需的干土和水泥质量，然后充分搅拌均匀，最后加入所需的去离子水后再搅拌。在制样机上采用变速率的两头压实法制取直径为61.8 mm、不同高度的圆柱试样。严格控制整个制样过程在30 min内完成。将制好的试样用保鲜膜包裹，放入恒温箱中养护7 d。随后将试样装模，放入饱和缸进行抽真空饱和。将饱和后的试样置于-30 ℃的恒温箱中快速冻结48 h，试样冻结完成后拆模，最后将其放在试验设定温度下恒温12 h后进行试验。

1.2 试验方案

为研究尺寸效应和加载速率效应对冻结水泥土力学特性的影响，进行了如下试验：

(1)相同直径不同高度试样的单轴压缩试验。温度设定为-10℃，试样直径为61.8 mm，高度分别为50，75，100，125，150 mm。试验采用位移控制加载方式，加载速率为3.75 mm/min。每组重复3次试验，共计15个试样。

(2)不同温度、不同加载速率的单轴压缩试验。温度设定为-1，-3，-5，-10，-15，-20 ℃共6个水平，试验仍采用位移控制加载方式，加载速率设定为5.0×10-3，5.0×10-4，5.0×10-5，5.0×10-6s-1共4个水平。每组重复3次试验，共计72个试样。

2 尺寸效应单轴压缩试验结果及分析

2.1 不同高径比试样应力-应变曲线

不同高径比冻结水泥土试样单轴压缩试验部分应力-应变曲线结果如图2所示，图中H和D分别为水泥土试样的高度和直径。从图2可以看出，不同高径比的冻结水泥土试样的应力-应变关系均为应变软化型，取峰值应力作为单轴抗压强度σmax，其对应的应变为破坏应变εf。参考已有研究，取应力-应变曲线上近似直线部分的平均斜率为冻结水泥土的切线模量E；把曲线斜率发生明显转折的点定义为起始屈服点，与之对应的应力和应变则定义为起始屈服强度σy和起始屈服应变σy，两者之比定义为起始屈服模量E0。

朱元林等[22]根据冻土的单轴压缩应力-应变曲线有无明显的弹性屈服点将其划分为两种基本类型：无明显弹性屈服的黏弹塑性类型和有明显弹性屈服点的弹塑性类型。结合图2可知，当高径比较小时，H/D=0.81，冻结水泥土试样的应力-应变曲线呈连续的应变硬化-软化，无明显的弹性屈服，应力-应变关系属于黏弹塑性类型。随着高径比增加，H/D=1.21，1.62，2.02，2.43时，冻结水泥土试样的应力-应变曲线均有明显的弹性屈服点，弹性屈服后呈现出连续非线性应变硬化-软化的特点。从以上分析可知，试样高径比影响冻结水泥土的单轴压缩应力-应变曲线类型。此外，从图2还可以看出，高径比明显改变试样峰后的变形特性，随着试样高径比的增加，峰后脆性增强。分析认为是由于单轴压缩时，试验机压头与试样端部之间的摩擦力使得试样上下端部附近形成了三维压缩应力区，试样高度越高，端部效应对试样中部横向变形约束影响越小，试样中部受力越接近一维压缩应力状态，峰值后的剪切滑移大大减小了试样的有效承载面积，导致试样峰后脆性增强[9，23]。

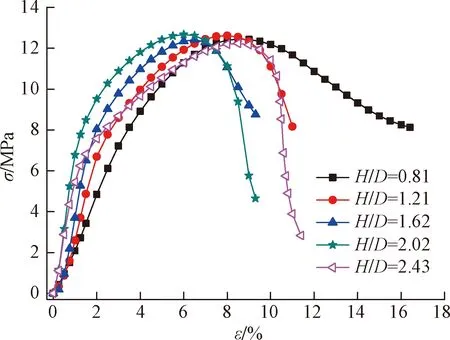
图2 同直径不同高度试样的应力-应变曲线

2.2 试样高径比对破裂形式的影响

相同直径、不同高度冻结水泥土试样单轴压缩破坏形式如图3所示。

图3 不同高度试样的破坏形式

从图3可以看出，当高径比较小时，H/D=0.81，试样破坏形式较为复杂，沿轴向出现较多的劈裂面；随着高径比增加，H/D=1.21，1.62，2.02，2.43时，试样基本呈剪切破坏。其原因仍可用上述端部效应造成试样内部应力非均匀分布来解释。值得一提的是，当H/D=2.43时，3个试件均出现较大弯曲变形。

2.3 试样高径比对力学参数的影响

冻结水泥土单轴抗压强度、切线模量、起始屈服模量、破坏应变随高径比变化如图4所示。从图4可以看出，随着高径比增加，冻结水泥土试样平均单轴抗压强度略有减小，但变化趋势不明显，二者关系可用抛物线进行拟合。H/D从0.81增加到2.43时，试样平均单轴抗压强度从12.8 MPa降低至12.4 MPa，降低幅度仅为3%。尤其是H/D在1.62～2.43时，试样平均单轴抗压强度几乎不变化，即试样单轴抗压强度不受尺寸效应影响。对岩土材料强度尺寸效应的机理通常采用材料内部缺陷的统计分布和端部效应来解释。一般认为岩土材料内部含有不同尺度的微缺陷，试样尺寸越大，其内部所含微缺陷的概率也较大，其强度就较低。试验结果也说明了制做的水泥土试样比较均匀，其强度的尺寸效应主要是由于端部摩擦引起。当H/D大于1.62时，可认为试样内部应力分布较为均匀，其单轴抗压强度基本稳定。从图中还可看出H/D越大，试验所得单轴抗压强度结果离散性也越大。

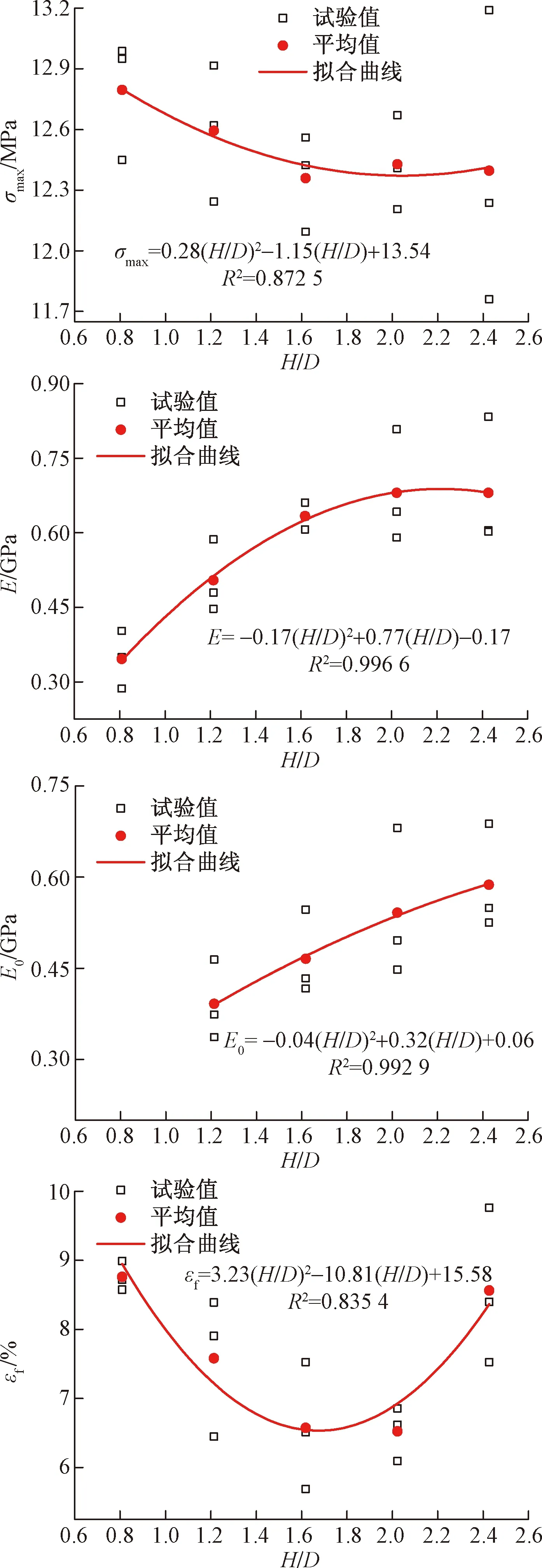
图4 力学参数与高径比的关系

冻结水泥土试样的切线模量和起始屈服模量均随高径比的增加而增加，其关系可用抛物线进行拟合。同样，当H/D在1.62～2.43时，切线模量和起始屈服模量变化量值均较小。

冻结水泥土试样的破坏应变随高径比的增加呈先减小后增加的变化趋势。H/D为1.62，2.02时，破坏应变分别为6.57%、6.52%，其值基本不受H/D影响。当H/D为2.43时，其破坏应变为8.56%，从其破坏形式可以看出是由于较大弯曲变形导致其破坏应变较大。

综上可知，当H/D在1.62～2.43时，冻结水泥土单轴压缩破坏形式和力学参数基本不受试样高径比的影响，但当H/D=2.43时，试验结果离散性较大且压缩过程中易弯曲。建议冻结水泥土单轴压缩试验试件高径比在1.62～2.02之间。

3 加载速率效应单轴压缩试验结果及分析

3.1 应力-应变曲线

在本试验设定的温度和加载速率条件下冻结水泥土的应力-应变关系均为应变软化型，按照朱元林等[22]对冻土的单轴压缩应力-应变关系划分属于弹性-连续非线性应变硬化-软化型。以-10，-15 ℃冻结水泥土在不同加载速率条件下的应力-应变曲线为例(图5)，加载速率越大，应力-应变曲线上的弹性屈服越明显，弹性屈服后表现出明显的非线性硬化特点。对应力-应变关系可采用如下模型描述[24]：

(1)

式中：a，b，c——试验参数，拟合结果列于表1。

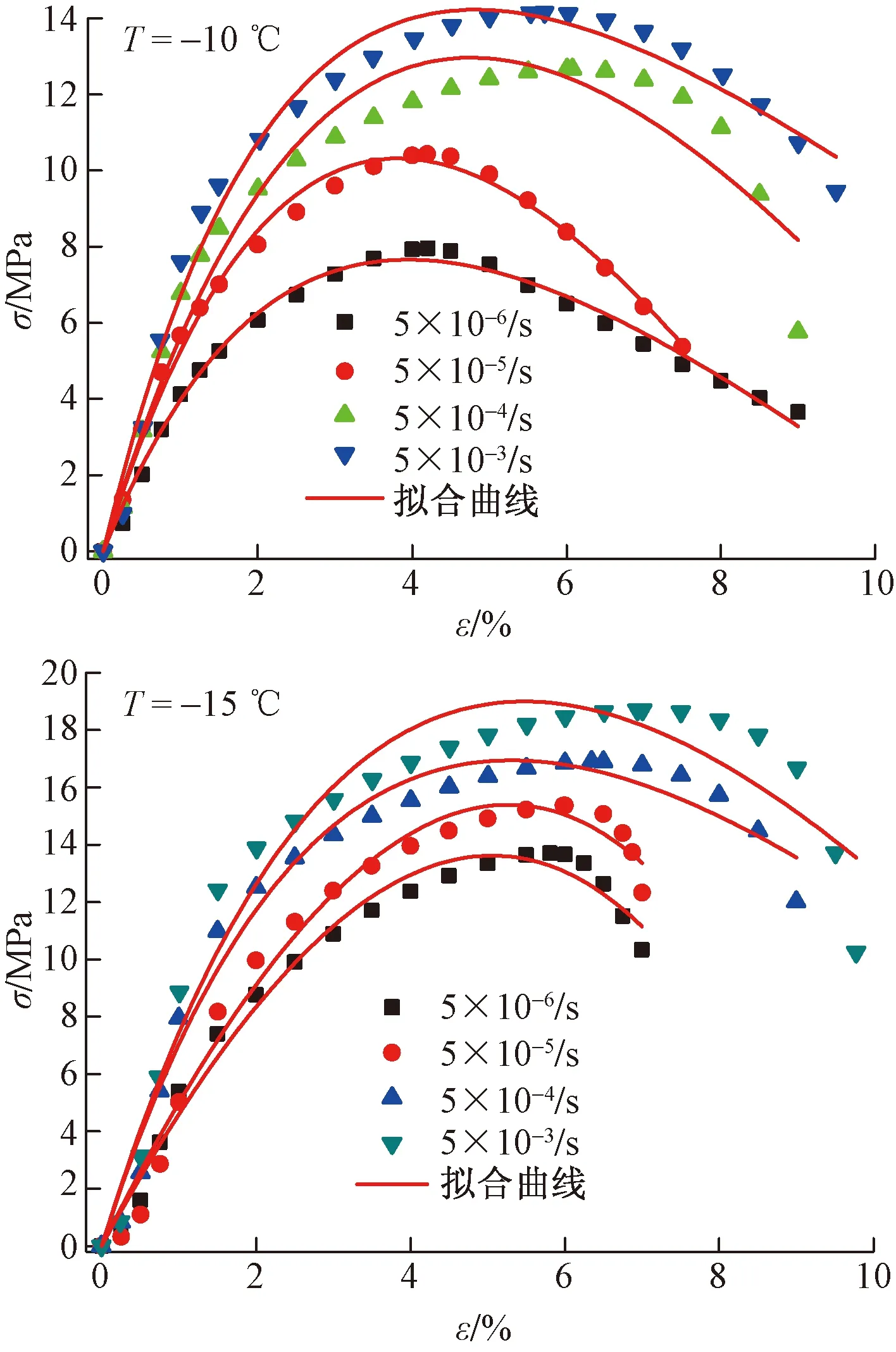
图5 不同温度下的应力-应变曲线

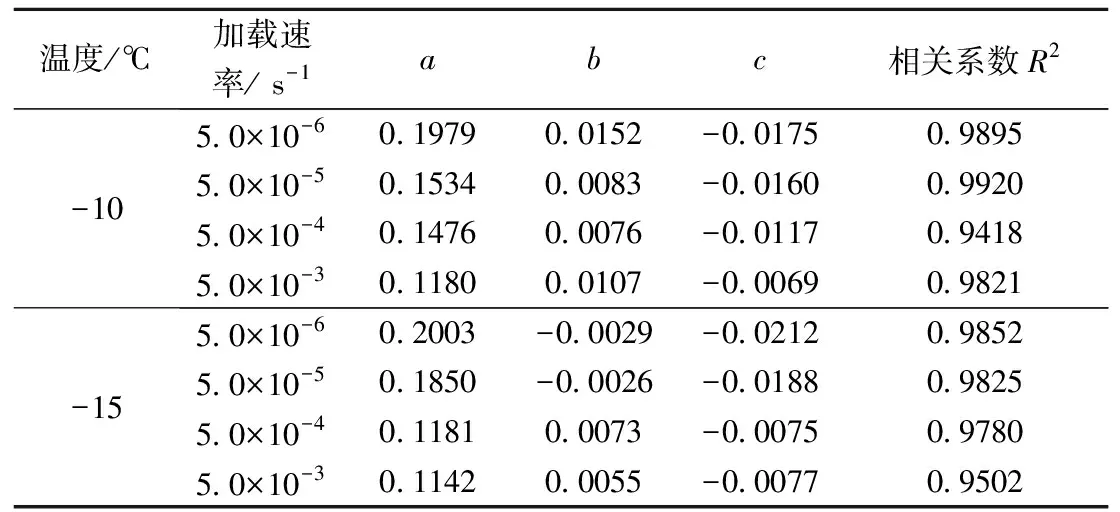
表1 式(1)中参数值

由表1可知，参数a与温度和加载速率有关，其值随着加载速率的增大而缓慢减小；参数b和c的值较小，c值均为负值。

3.2 抗压强度与加载速率、温度的关系

图6为不同温度条件下冻结水泥土单轴抗压强度与加载速率双对数坐标图。从图6可以看出，冻结水泥土单轴抗压强度随加载速率增加而增大。温度越低，抗压强度越大，加载速率对抗压强度的量值的改变也较大。加载速率从5.0×10-6s-1增加到5.0×10-3s-1，温度为-1 ℃时，冻结水泥土单轴抗压强度从3.13 MPa增加到5.33 MPa，增加了2.2 MPa；温度为-15 ℃时，冻结水泥土单轴抗压强度从15.7 MPa增加到21.2 MPa，增加了5.5 MPa。

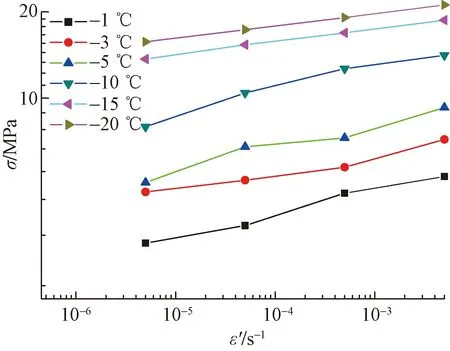
图6 单轴抗压强度与加载速率关系曲线

由图6可知，不同温度条件下冻结水泥土单轴抗压强度与加载速率的关系可用幂函数进行拟合[22]：

(2)

式中：A，m——和温度有关的参数，拟合结果如表2所示；

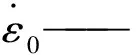
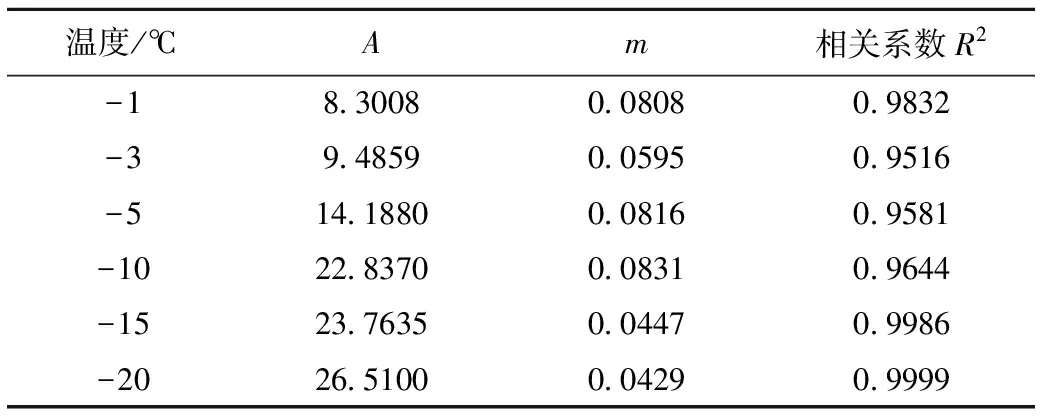
表2 式(2)中参数值

从表2可以看出，参数m值较小且受温度的变化影响较小；A值随温度的降低而增大且变化幅度较大。如图7所示，参数A与温度线性相关：

A=-1.0108T+8.4172

(3)

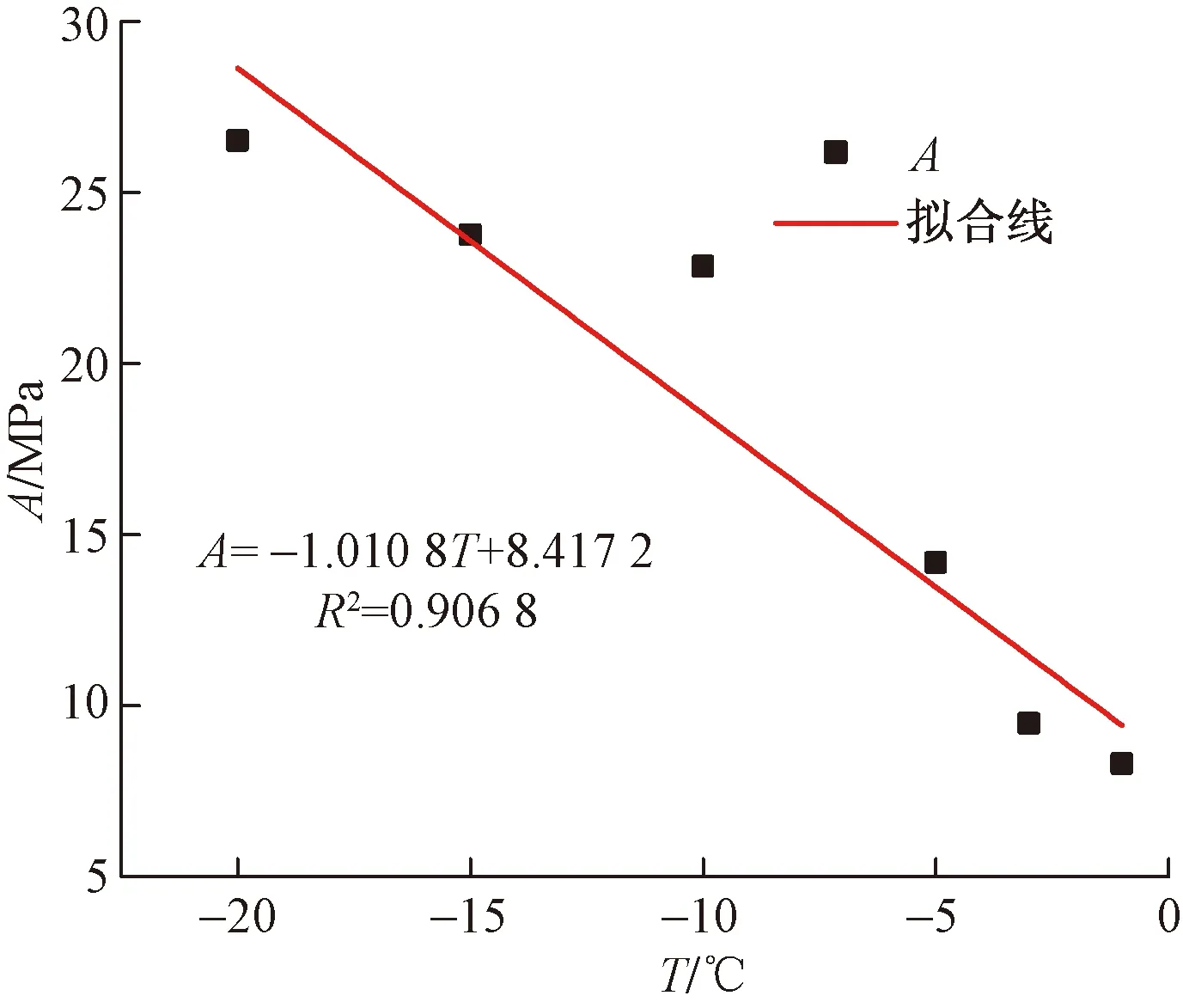
图7 A和温度关系曲线

由式(2)、式(3)可得到考虑温度和加载速率影响的冻结水泥土单轴抗压强度表达式：

(4)

基于统计学理论和结构风险最小化原则的支持向量机非常适合处理小样本的分类和回归问题。随机选取21组样本对支持向量机进行训练，其余3组作为测试样本，作为对照来评估式(4)的准确性。表3为式(4)回归值和支持向量机预测值与单轴抗压强度试验值比较，可以看出回归值和支持向量机预测值均具有较高准确度。

表3 抗压强度实测值与预测值比较

3.3 起始屈服强度与加载速率、温度的关系

起始屈服强度也是材料的重要力学参数，以下考察加载速率和温度对冻结水泥土起始屈服强度的影响，如图8所示。

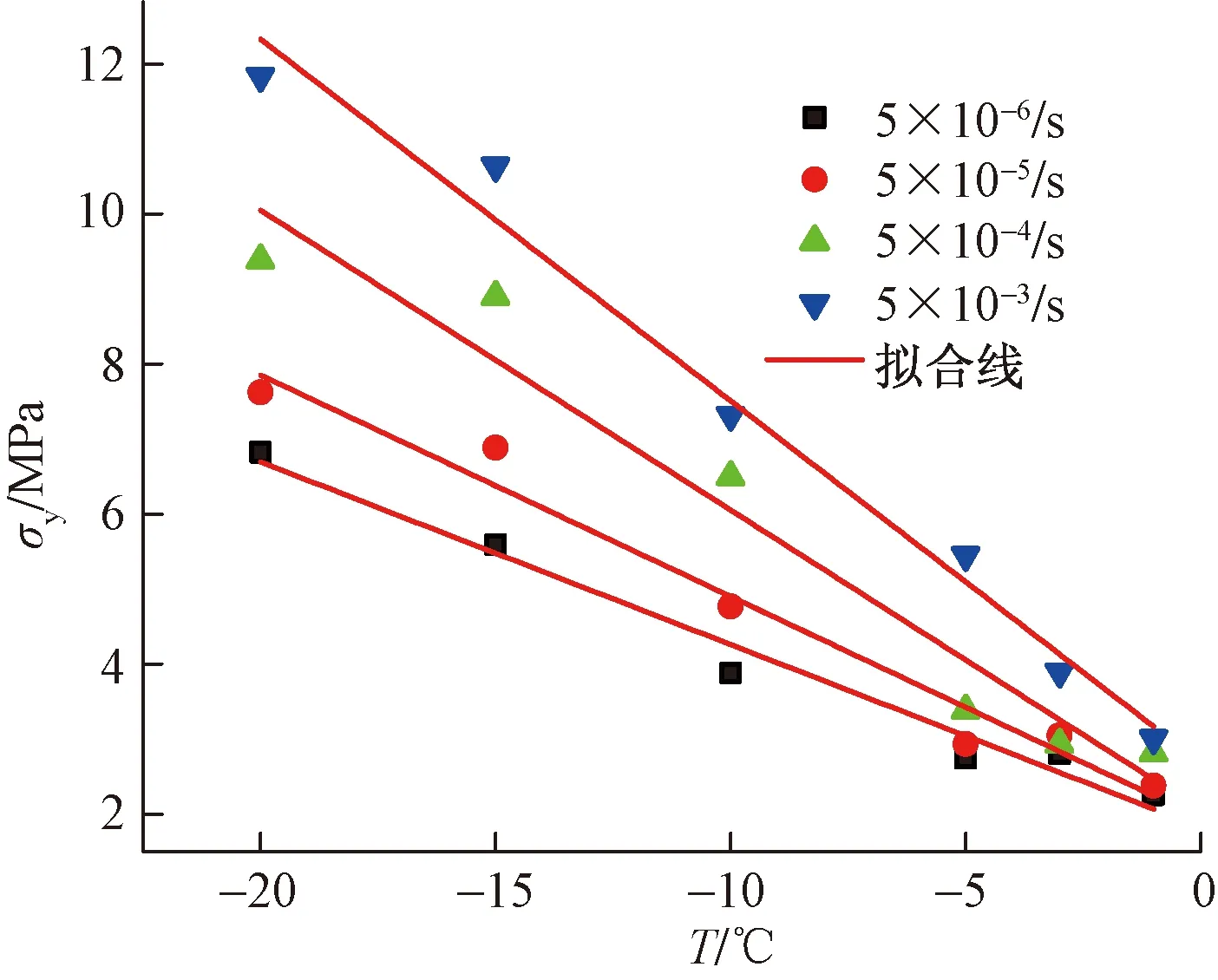
图8 起始屈服强度与温度的关系

从图8可以看出，与冻结水泥土单轴抗压强度类似，起始屈服强度随温度的降低和加载速率的增加而增大，温度越低，起始屈服强度受加载速率影响越大。不同加载速率条件下起始屈服强度与温度的关系可用线性函数拟合，如式(5)所示，拟合结果如表4所示：

σy=KT+d

(5)

式中K，d为试验参数，拟合结果列于表4。

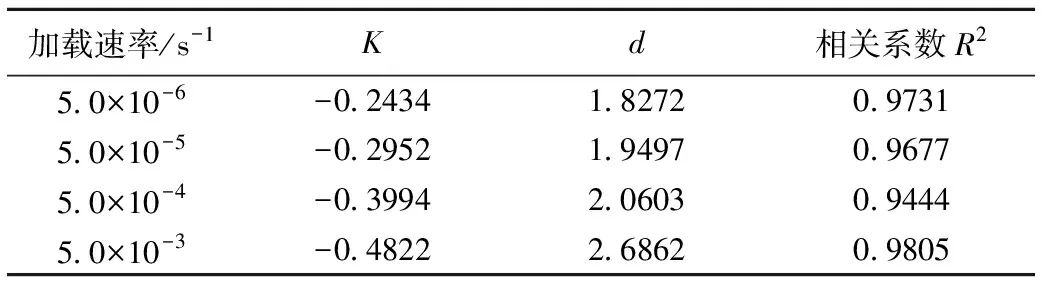
表4 式(5)中参数值

从表4可知，加载速率越大，K的绝对值越大，d值越大。将冻结水泥土起始屈服强度与单轴抗压强度之比定义为屈强比δ。δ值较大，表明材料脆性破坏明显。不同加载速率条件下屈强比δ与温度的关系如图9所示。从图中可以看出，除个别数据外，δ在0.4～0.6之间。从整体来看，加载速率越大，δ越大，其值几乎不随温度变化而改变，如加载速率为5.0×10-3s-1时，δ在0.55左右。当加载速率较小时，温度高于-5 ℃时，δ随温度变化有明显变化。温度低于-5 ℃时，可以认为屈强比不受温度影响，加载速率越大，屈强比越大。

图9 屈强比(δ)与温度(T)的关系

3.4 切线模量与加载速率、温度的关系

不同加载速率条件下冻结水泥土切线模量随温度变化规律如图10所示。

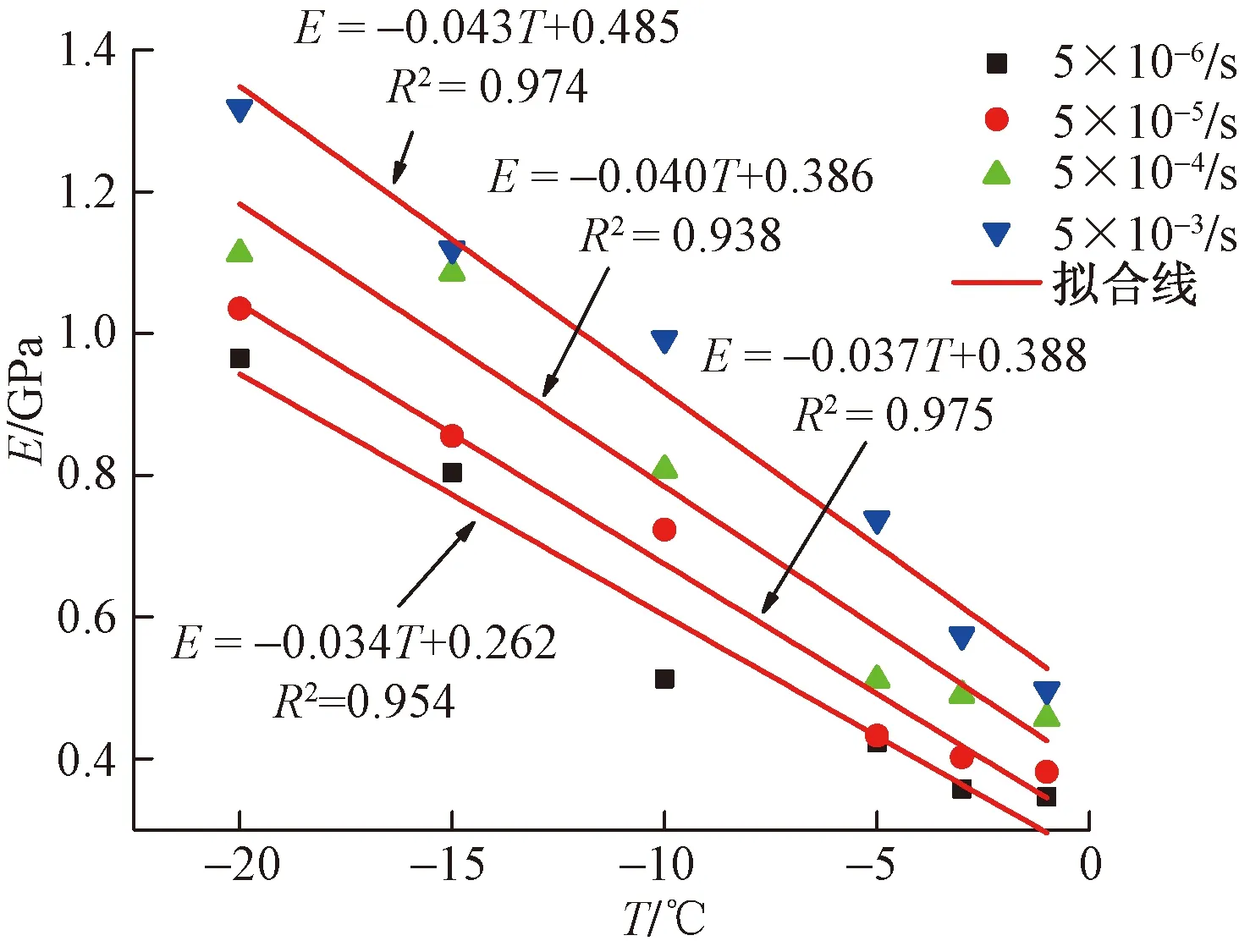
图10 切线模量与温度的关系

由图10可以看出，切线模量随着温度的降低和加载速率的增加而增加。不同加载速率条件下切线模量与温度线性相关，拟合关系式及相关系数列于图中，拟合关系式的参数与加载速率有关。温度越低，加载速率越大对切线模量影响越大。如温度为-1 ℃时，加载速率从5.0×10-6s-1增加到5.0×10-3s-1，切线模量在0.35～0.50 GPa之间变化，变化量值仅为0.15 GPa；温度为-20 ℃时，随着加载速率增加，切线模量变化量值为0.36 GPa。反映到拟合参数上就表现为加载速率越大，拟合直线斜率绝对值越大。

3.5 破坏应变与加载速率、温度的关系

图11为不同加载速率条件下冻结水泥土破坏应变随温度变化的双对数曲线。

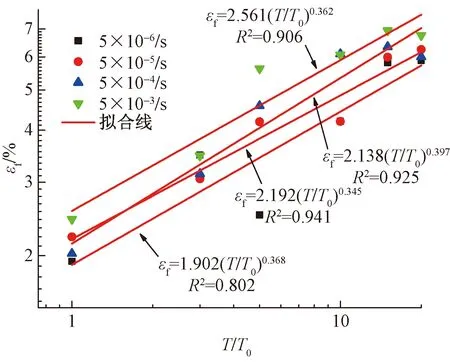
图11 破坏应变与温度的关系

由图11可知，在试验设定温度和加载速率条件下，水泥土破坏应变在1.94%～6.94%之间变化。参考关于冻土单轴抗压试验的研究可知[15-16]，水泥土破坏应变明显小于相同试验条件下的冻土破坏应变，说明水泥的加入使得材料的塑性变形减小。温度越低，冻结水泥土破坏应变越大，不同加载速率条件下，破坏应变随温度降低呈现出先迅速增大后缓慢增大的非线性变化趋势。温度低于-15℃时，随着温度继续降低，破坏应变略微改变，但变化量很小。如加载速率为5.0×10-6s-1时，温度为-15 ℃时破坏应变为5.81%，温度为-20 ℃时破坏应变为5.88%。相同温度条件下，从整体来看，加载速率越大，破坏应变越大，但差别不明显，温度较高和温度较低时，这种差别可忽略。不同加载速率条件下冻结水泥土破坏应变与温度的关系可用幂函数进行拟合，如式(6)所示，拟合参数列于图11中。

(6)

式中：T0——参照温度，取-1 ℃；

B，n——与加载速率有关的参数。

从图11可以看出，不同加载速率条件下的B，n值差别不大，B值在1.90～2.56之间变化，n值在0.345～0.397之间。