城市暴雨内涝灾害风险模糊综合评价体系构建研究
2019-12-09张玉华
张玉华,蔡 甜
(中国电建集团中南勘测设计研究院有限公司,湖南 长沙 410014)
近年来,内陆地区出门“看海”已不再是人们茶余饭后的谈笑,逢雨必涝成为诸多城市的诟病。深圳“20140330暴雨”致使部分区域积水深度逾1.5m,北京“20150721暴雨”导致超过1.5万km2城区面积受淹,不少低洼处停放的轿车升级为“潜水艇”。2016年7月6日武汉中心城区全城内涝,88处发生严重积水,华中科技大学成为“知识的海洋”。2017年6月23日暴雨夜袭南昌,进外路、南京西路等道路发生覆盖性洪水,沿途车辆均被阻滞,南昌火车站的楼梯通道成为室内“瀑布”。可以看出,频发内涝灾害轻则影响到城市的日常运行,严重的话直接影响到人民的生命财产安全。国内一些学者也针对内涝灾害做了许多风险评估方面的研究,总的来说,探寻及建立一个有效的内涝风险评估体系和防治系统成为当今政府和科研、工程人员的工作热点。
1 灾害风险理论介绍
广义上将,灾害风险就是对灾害可能造成的损失。灾害风险理论认为灾害是由危险性(H)、敏感性(E)、脆弱性(S)三大因素构成,其中H是风险产生的充分条件,S为必要条件,E为风险的背景条件。以暴雨内涝灾害为例,危险性是对灾害强度、范围、频次的特征描述,如降雨强度、积水深度、受灾面积等。危险性是产生风险的首要条件,一般看作直观性风险。脆弱性是指承灾体在灾害发生后的止损性能力,人类作为承灾体的最重要主体,脆弱性可看作人类的年龄、性别组成、经济情况、医疗卫生及应急救援能力。承灾体作为灾害的被动接受者,其脆弱性强度将起到对灾害风险的放大或缩小作用,直接影响到灾害风险的大小。敏感性是指人类赖以生存的“自然-社会”环境对灾害风险形成具备敏感的致变作用,如管网密度、地形高差、地形起伏的细微变化将直接影响地面积水情况的分布,进而改变灾害的风险等级。通过以上描述,灾害风险(R)也可以表述为由H、E、S的交集构成的集合,如图1所示。
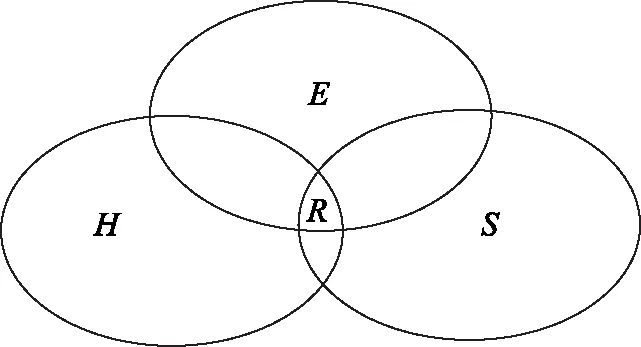
图1 灾害风险构成图
2 模糊综合评价原理及步骤
2.1 模糊数学与模糊集合
2.1.1模糊数学的概念
在传统的数学集合论中,一个指定的集合和对象,通常将二者的关系描述为对象要么属于这个集合,要么一定不属于这个集合。这种“非此即彼”的关系体现了数学的确定性,成为经典数学的明显特征。确定性的描述有着准确、直观的优势,便于辅助人们判断事件的特征和属性。但是,在日常生活中存在很大难以准确判断的事件。比如人们评价事物“胖与瘦”、“亮与暗”等特征时,很难有一个准确的评价标准。于是我们会加入有“偏瘦、很瘦、微胖、超胖”以及“黑暗、微亮、透亮”等模棱两可的描述词,这些描述词体现了事件对象的不确定性,即模糊性。
模糊数学由模糊集合衍生,其在数学、机械电子、地理信息、环境科学等相关领域得到了较好的应用。模糊数学的精髓是“隶属度函数”概念的引入,隶属度可以理解成“非此即彼”关系的缓和,即其试图在“此”和“彼”的关系过渡中建立界定关系的“刻度”。暴雨内涝灾害风险本就是一个不确定性问题,因此模糊数学可以恰当地对其进行表述。
2.1.2模糊集合
模糊集合的出现就是为了弥补经典集合中对于模糊性元素隶属关系判定的劣势,模糊集合可具体这样描述:定义A为论域U上的一个集合,x为集合中任一元素;再定义uA为集合A的隶属度,uA(x)为任意x与A对应的隶属度值,且uA(x)∈[0, 1]。集合A的隶属度值可以表达为下式:
(1)
上式得出:当uA(x)=0时,认定元素x不属于A。当uA(x)=1时,则认定x属于A。当uA(x)∈(0,1)时,则认为x可能属于A,也可能不属于A。uA(x)越接近于1,说明x更优先隶属于A,即更倾向属于A;uA(x)越接近于0,则说明x更倾向不属于A。
2.2 隶属度函数和权重系数
2.2.1隶属度函数
隶属度函数是描述元素特性与元素集合隶属度关系的一种数学方法,是模糊特性转向定量分析的预处理过程,故而隶属度函数的确定成为模糊集合论展开的重要步骤。由于模糊集合中的元素具有差异性,且元素的特性也具有多样性,所以尝试找到一个普适性的隶属度函数来描述各个元素和特性是不现实的。对于暴雨内涝风险,由于大多数指标和风险呈线性关系,因此常采用升、降半梯形、三角形分段函数作为隶属度函数,其函数图像见图2。
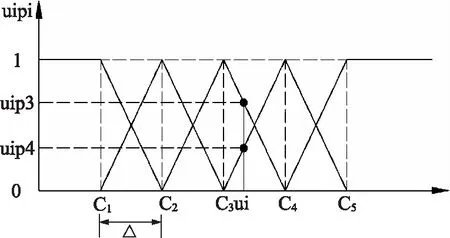
图2 分段隶属函数的图像
图2的横坐标为指标的间断点,纵坐标为指标ui与风险等级pi相对应的隶属度uipi。由图2可以看出,对于C3、C4之间的ui指标有两个纵坐标值uip3、uip4,且uip3明显大于uip4。这说明ui对p3(中度风险)的隶属度高于p4(较高风险),按照最大隶属度原则,也就是说ui更倾向于评估为较高风险。
2.2.2权重系数
本文以层次分析法确定指标的权重矩阵和系数。层次分析法将目标问题看作多因素的结果,这些因素分层次阶梯隶属,同级因素又相互联系、共同作用,最后形成层次结构体系。层次分析法需将目标问题A分为目标层、准则层、指标层三层结构,然后赋予权重矩阵并计算权重系数。权重矩阵需进行一致性校验,其过程如下:
(1)一致性校验。以n阶权重矩阵为例,其一致性指标表示如下:
(2)
式中,λmax为最大特征根。
(3)
式中,C.R为一致性比例;R.I为随机一致性指标(可查随机一致性指标计算表)。
若C.R值≤0.1,则认为矩阵满足校验条件。否则,需重新赋予i、j标度值以校验矩阵。
2.2.3模糊综合评价步骤
模糊综合评价法是一种逻辑性较强的多指标评价法,其主要流程如下:
(1)创建目标问题的因素集合U=(u1,u2,…,ui),其中i为因素个数。
(2)建立目标问题的评语集合P=(p1,p2,…,pj),其中j为评语级数。
(3)确定各因素的隶属度函数F=(f1,f2,…,fj),其中f为子隶属度函数。
(4)构建模糊矩阵R,即隶属关系矩阵。模糊矩阵R是集合U中的各因素对集合P中的各评语等级的隶属度,故而矩阵R的阶数为i×j,其形式如下式:
(4)
(5)按照前文方法,确定权重矩阵A:
A=(A1,A2,…,Ai)
(5)
(6)将权重矩阵和模糊矩阵进行复合计算,通常采取乘法运算,得到复合模糊矩阵B:
B=A○R
(6)
式中,○为模糊算子,取M(•,⊕)。
(7)按最大隶属度原则对矩阵B进行最大隶属度计算,作出模糊综合评价。
模糊综合评价法的技术流程见图3。
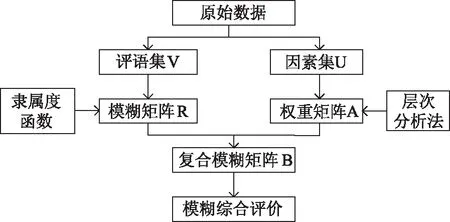
图3 模糊综合评价法技术流程
3 城市暴雨内涝灾害风险评价指标体系
模糊综合评价法是指标体系法的一种评价方法,可对指标体系的各指标进行定性与定量分析。从灾害风险理论得出,“暴雨内涝风险”这一目标问题是多指标、多因素共同作用的集合,且各指标关系错综复杂,涉及领域广泛。因此,在进行暴雨内涝风险分析时,就要将这一目标进行指标分解、各指标关系及权重梳理,最后再构建完整的指标结构体系。指标体系的构建是一个严谨而精细的过程,指标的选取方法、指标的结构层次以及指标的量化准则直接关系到指标体系的评价结果。
3.1 指标选取原则
指标选取的方法和原则对于指标体系的评价结果的好坏起着基础性和决定性作用。因此,指标体系在选取指标时应符合以下原则:
(1)系统性及全面性原则。暴雨内涝灾害是一个复杂而庞大的系统,而暴雨内涝风险又具备“自然-社会”双重属性。所以在进行指标选取时应以灾害风险理论为依据,全面考虑危险性、敏感性、脆弱性这三大风险因素,综合体现暴雨内涝风险的内在因素。
(2)客观性及代表性原则。在日常生活中,由于个人的认知能力有限,可能对某一事物的认知存在局限,导致认知不全面。客观性就是指在选取指标时要避免由于局限的认知所导致的主观臆断,以偏概全。因此,在指标选取时应该客观调查,集思广益,如通过问卷调查法和专家头脑风暴法对指标进行筛选。代表性是指选取的指标应能明显地反映暴雨内涝风险的本质特征,暴雨内涝风险有多种因素构成,如果全部纳入指标体系,则涉及到极为庞大的数据与逻辑关系。所以,就要对这些因素进行关系梳理,分清隶属关系和主次影响,选择有代表性的因素作为指标体系的构成指标。
(3)可获得及可操作性原则。用于构建指标体系的指标,其数据应便于收集,如通过水利志、影像遥感等方式获得数据,即数据的可获得性。指标的可操作性指用于评价体系的指标之间应有可比性,且最终能够在统一的平台和工具中实现数据处理和比较。
(4)可量化性原则。指标体系的最终成果是目标问题的定量或半定量评价。因此,实现这一成果的前提是指标的可量化性,这就要求各指标的计量单位应符合国家或国际上的计量规定。
(5)普适性原则。本指标体系的评价对象为城市暴雨内涝风险,指标的普适性指其对这一范畴的通用性。因此,要求被选取的指标为研究对象的通用属性,不因地域差异出现指标不适用的情况。
3.2 指标体系建立
3.2.1层次结构划分
城市暴雨内涝风险模糊综合评价指标体系是一个多指标系统,通过目标问题分解、指标关系梳理,最终可将指标体系构建成三个层级:
(1)目标层:即拟解决的目标问题集,以暴雨内涝的风险等级为目标层,反映的风险大小。
(2)准则层:即组成目标问题的因素类指标集,在本指标体系中,暴雨内涝风险由危险性、敏感性、脆弱性三大因素组成,故将其作为准则层。
(3)指标层:即基础性指标集,隶属于准则层中各因素类指标集。指标层中的指标是实现目标问题的基础,按照隶属类别可分为:以积水情况为一类的致灾因子指标,以下垫面属性为一类孕灾环境指标和以社会、经济因素为一类的承灾体指标。
3.2.2指标选取
积水情况属于致灾因子危险性指标,它反映暴雨内涝灾害的直接风险,由积水深度、积水面积、积水时间三个指标组成。积水深度体现了地表产、汇流能力和排水管渠过流能力的差值,暴雨灾害风险很大程度上取决于积水深度的高低。积水时间体现了暴雨灾害持久性和时效性,而积水面积则反映了暴雨灾害风险的时空分布和作用范围。
孕灾环境敏感性指标代表了下垫面的属性,它由地面高程、不渗透率、地形坡度三个指标组成。一般来说,地面高程较低的区域更易积水,即地面高程也会影响到于暴雨灾害的风险值。不渗透率体现了下垫面的透水能力,不渗透率较高的区域可能面临更大的积水风险。地面坡度一方面决定了洪水的流向,另一方面决定了洪水的流速,坡度陡的区域蕴含了更大的灾害风险。
承灾体脆弱性指标以社会经济和人身安全为考量依据,包含建筑密度和兴趣点密度两个指标。城镇的人口的流动性增加了人口密度的获取难度,而建筑是人类居住和工作的场所,所以在本次研究中,采用建筑密度侧面体现人口密度。笔者将城市的工、商、学、医等单位定义为为兴趣点,兴趣点密度则为单位面积上的兴趣点个数。兴趣点密度体现了区域的经济繁荣程度和减灾能力,如果学校、医院、厂区等区域受淹,城市的社会经济和居民的人身安全将难以保障。
综上所述,城市暴雨内涝风险模糊综合评价指标体系将积水深度、积水面积、积水时间、地面高程、不渗透率、地面坡度、建筑密度、兴趣点密度八个指标纳入指标体系,建立的指标体系结构如图4所示。
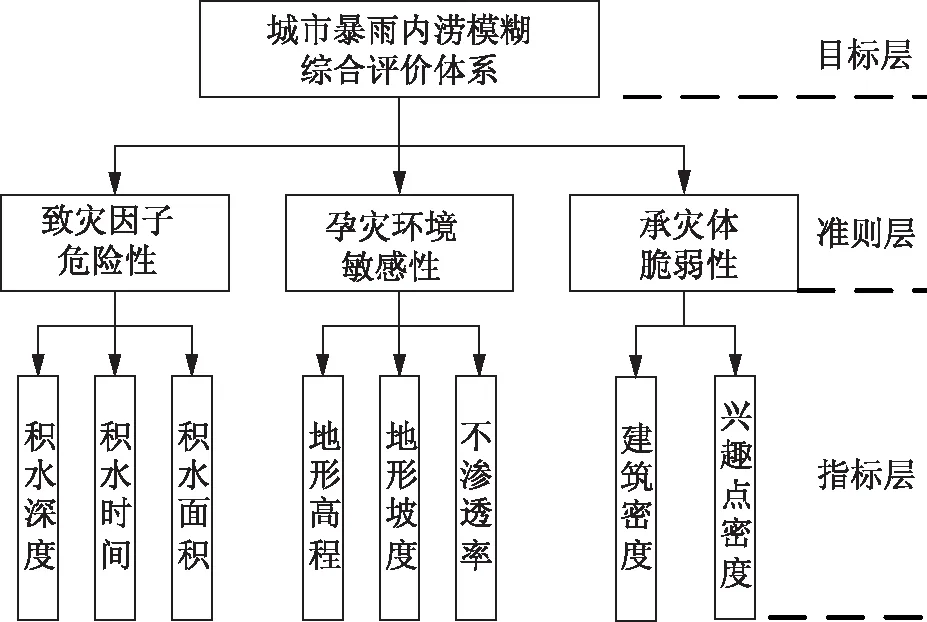
图4 城市暴雨内涝风险模糊综合评价体系
3.3 指标体系定量评价
依据层次分析法的计算原理和上一小节的构建的指标体系,本指标体系的所确定的指标层和准则层权重系数如下:
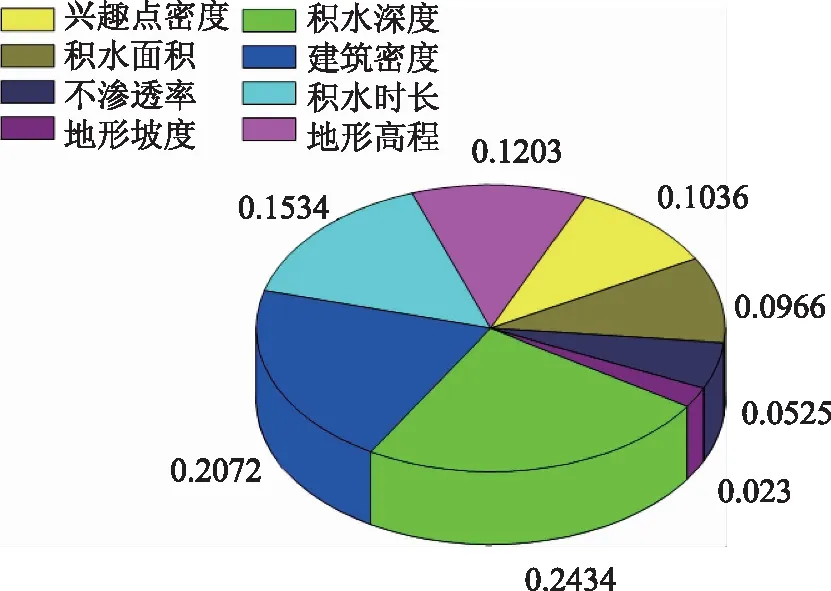
图5 指标层权重图

图6 准则层权重图
由图5、图6可以看出,指标层八个指标积水深度的权重最大,为0.2434,地面坡度的权重最小,为0.0230;准则层中危险性的权重最大,为0.4934,敏感性的权重最小,为0.1958。以上权重均在值0.1的情况下求得,说明权重的计算结果合理。
对于隶属度计算和风险等级划分,由于指标的多样性决定了指标单位的迥异性,如积水深度的单位是m,而积水时间的单位是h或min。这就要求多种指标需采用归一化方法处理,从而使各指标无量纲化,最终才能进行指标的定量计算和评价。而升、降半梯形、三角形分段函数刚好能将各指标归一化,且可以根据间断点计算各指标对于不同风险等级的隶属度。隶属度计算后,按照最大隶属度原则对八个指标进行权重和隶属度的叠加计算,从而确定每个区域的风险等级。
4 结论与建议
暴雨内涝灾害是一种常见的自然灾害,风险评价的目的是为了尽可能地辅助决策者减灾、避灾。由于暴雨内涝灾害风险是气象、下垫面、人文及经济多重因素共同作用的结果,因此在构建指标体系时应全面考虑指标间的关系,筛选出最具代表性的指标。由于指标权重对风险评估结果有着至关重要的影响,所以在确定权重时应进行多方专家论证和打分。此外,由于模糊综合评价法与内涝风险的不确定性有着很高的契合度,因此模糊综合评价法在内涝风险评估方面具备很大的优势。
