可控移相器附加阻尼控制器设计研究

2019-12-09付俊波常宝立王新宝黄志光

浙江电力 2019年11期

付俊波，常宝立，曹路，王新宝，黄志光

（1.南京南瑞继保电气有限公司，南京 211102；2.国家电网华东电力调控分中心，上海 200120）

0 引言

随着用电负荷的持续增加，输电网也得到了快速发展，尤其以长距离、大功率的电能输送特点在输电网中表现得尤为明显。这种输电结构导致区域间电网容易出现低频振荡问题，成为限制电网输送容量且影响电网安全稳定运行的因素之一。针对低频振荡问题，常规的手段通常采取限制开机减少功率输送的方式或者事故后切机措施，但这些方式对系统经济运行不利，为了满足系统运行对低频振荡的要求需要付出较大的代价。电力电子技术的发展为解决这类问题提供了新的解决思路，如统一潮流控制技术、可控串补、柔性直流输电技术均可用于解决电网的低频振荡问题。但阻尼控制器的信号选择是阻尼控制器设计需要考虑的重要因素，文献[1]中提到了统一潮流控制器的阻尼控制方法，用于限制低频振荡的问题，但没有明确附加阻尼控制的输入优劣比较，且统一潮流控制器造价昂贵。文献[2]研究了TCSC（可控串联补偿装置）的低频振荡控制器设计方法，对可控移相器的阻尼控制研究具有一定的借鉴意义，但也未明确阻尼信号的优劣选择。文献[3]研究了可控移相器的本体建模，没有涉及到可控移相器的阻尼控制研究。从已发表的文献来看，对可控移相器的研究主要侧重于控制模型、系统应用等方面，对可控移相器的阻尼控制研究相对较少。晶闸管控制的可控移相器因为调节速度快，具备阻尼控制能力。但阻尼控制输入量众多，有电压、功率、频率等信号量，哪种输入量对可控移相器阻尼控制与设计效果更好，如何设计可控移相器阻尼控制函数是本文的研究重点。

1 可控移相器的基本原理

电网中2 个母线节点通过高压输电线路互联，忽略线路损耗时，线路上的有功潮流如图1所示。

图1 两个母线节点通过输电线互联

图1 可用公式表达为：

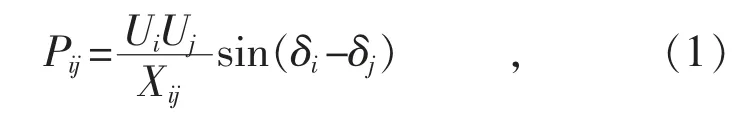
式中：Pij为节点i 流向节点j 的有功功率；Ui，Uj分别为节点i 和节点j 的母线电压幅值；δi，δj分别为节点i 和节点j 的母线电压相位；Xij为联络线路的等效电抗值[4]。

由式（1）可知，线路上传输的有功功率主要由节点电压、相角和线路阻抗决定，通过控制输电线路的电压、阻抗以及相角就可以改变线路传输的功率。在大型电网中，节点电压、幅值受很多因素的制约（如负载和设备的耐压等），一般在额定值附近变化不大，因此可通过调节电压相角来实现对有功潮流的调节[5]。

移相器是通过在输电线上串联一个幅值、相位均可调的补偿电压实现移相的装置。图2（a）为移相器的结构，ET（励磁变压器）提供三相输入电压，BT（串联变压器）输出三相补偿电压。如图2（b）所示，补偿电压Vp幅值和相位的变化，将改变V2的幅值和相位，从而控制输送的有功功率和无功功率[6]。

典型的移相器主要有两种类型，QBT（正交调节器）和PAR（相角调节器）。欧洲（尤其是英国）广泛采用QBT，而美国大部分采用PAR。如图3所示，PAR 的端口电压幅值相等（忽略损耗），而QBT 输出的补偿电压UT与输入电压相差输入度。

图2 移相器基本原理

图3 装有移相器的系统模型

2 可控移相器的类型选择

可控移相器由机械式移相器发展而来，利用电力电子器件替代有载调压机构，实现输出补偿电压的快速调节，可控移相器又可分为分级调节可控移相器及连续调节可控移相器。

2.1 分级调节可控移相器

高压大容量可控移相器的典型结构如图4 所示，其控制回路由有载调压机构替换为晶闸管换流阀，并联变压器的副边由多抽头型式更改为多绕组型式，每个绕组均与由4 组反并联晶闸管组成的桥接回路连接[7]。

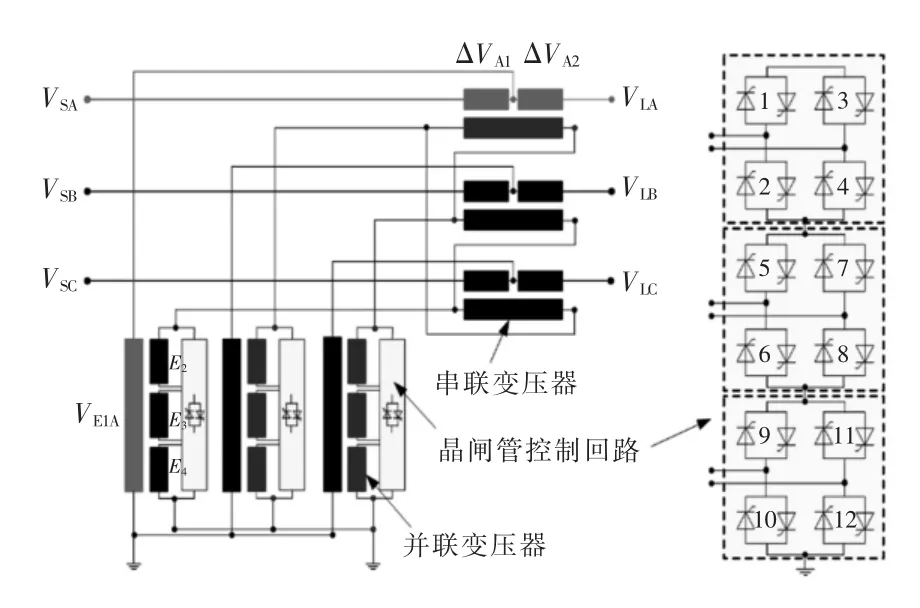
图4 分级调节可控移相器典型结构

图4 结构形式的可控移相器，其可调级数取决于并联变压器副边绕组的数量和变比，如2 个变比为1：3 的绕组，可调级数为±4 级；3 个变比为1：3：9 的绕组，可调级数为±13 级；可调级数越大，每级的调节精度越高，但同时变压器的绕组数量及电力电子器件的数量也随之增加，成本越高[8]。

分级调节可控移相器可实现补偿电压的快速调节，在满足系统稳态潮流控制需求的同时，可参与系统动态稳定的调节，如阻尼系统振荡、增强系统暂态稳定性等；其控制相对较简单，工作时无谐波，但只能实现分级调节，无法连续平滑调节。本文需要分析的可控移相器的阻尼控制也正是基于这一结构[9]。

2.2 连续调节可控移相器

连续调节可控移相器其变压器的主体结构与分级调节可控移相器类似，但其并联变及阀组的结构如图5 所示。

图5 连续调节可控移相器控制回路结构

并联变压器副边仅2 个抽头，分别与两组反并联的晶闸管阀连接，通过连续控制晶闸管SW1和SW2的触发角，使SW1和SW2轮流导通，可实现输出电压基波分量幅值在U1和U2之间连续变化[10]。

由于晶闸管需要过零关断的特性，因此对晶闸管的开通关断必须根据负载的状况合理控制，所需控制策略非常复杂；同时由于电压在U1和U2之间不停变化，会向系统注入大量低次谐波，必须相应安装滤波器；这种结构的可控移相器只能实现正向电压的输出，不能实现双向调节。因此连续调节的移相器无法用于实际工程中，仅作为理论研究[11]。

3 可控移相器的阻尼控制传递函数

从已发表的文献看，对这种电力电子设备进行低频振荡控制的主要有统一潮流控制器、柔性直流装备、可控串补、静止无功补偿器。它们的共同特点在于通过快速可关断的电力电子器件控制，可跟随低频振荡的频率响应。同样，基于晶闸管控制的可控移相器也可以通过对晶闸管的开通关断控制改变移相器的档位，进而改变可控移相器串入线路的电压和功率[6]。

图6（a）说明了用传输角控制实现阻尼功率振荡的控制效果和控制要求。图6（b）开始的一个功率下跌表示系统受到扰动的激励，并假定在这个扰动下引发了功率振荡。其中图6（a）为传输角在稳态值δ0附近的有阻尼和无阻尼控制振荡波形；图6（b）为传输功率P 围绕稳态值P0附近的有阻尼与无阻尼振荡波形[12]。

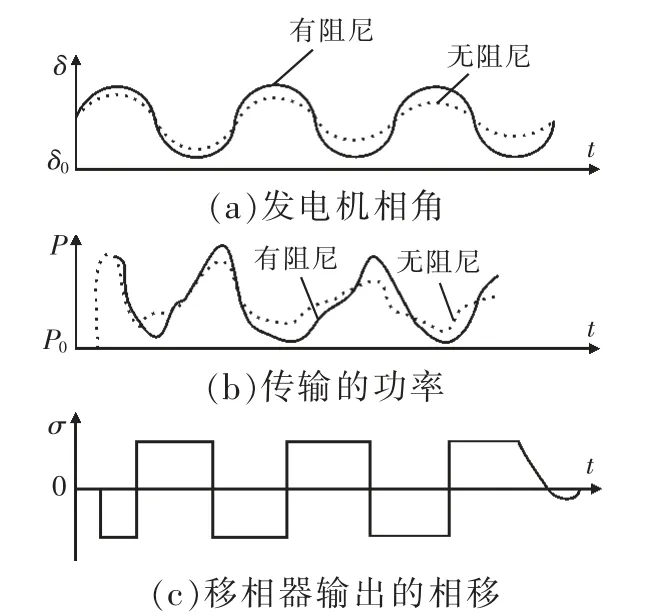
图6 阻尼振荡控制

设σ 角的运行范围为－σmin≤σ≤σmax，对应的δ 的变化范围为0＜δ＜π/2，则图6（c）表示移相调节作用对σ 角的控制输出。当dδ/dt＞0 时，σ 为负值，P-δ 曲线向左移，表示传输线受端传输角和传输功率的增加；当dδ/dt＜0 时，σ 为正值，P-δ曲线向右移，因此总的传输角和传输功率减少[13]。

可控移相器的附加阻尼控制的基本结构类似于电力系统稳定器的结构，传递函数由稳态信号隔直、相位超前补偿、稳定器增益和稳定器限幅环节四部分组成。

（1）稳定信号隔直：隔直环节可理解为高通滤波器，主要目的是滤出故障后的直流分量。

（2）移相环节：移相环节是所有设备设计控制时的主要环节，其目的是将阻尼控制的输入信号量通过相位的补偿后得到的输出能量与低频振荡的趋势相反，来有效抑制低频振荡。

（3）控制器的增益：增益环节对阻尼控制有着重要意义，增益的大小决定了向系统提供阻尼的作用的大小。

可控移相器的附加阻尼控制器的基本结构如图7 所示。X 为附加阻尼控制器的输入信号，一般可以取联络线功率波动、发电机转速、系统频率等作为附加阻尼控制器的输入信号。经过控制器转换为输出为移相角度，然后移相角度转换为档位来控制可控移相器[14]。

图7 可控移相器附加阻尼控制的基本结构

4 可控移相器附加阻尼控制参数设计

现有的机电暂态程序中，移相器的模型仅有带漏抗和移相角度的稳态模型，无法反映移相器的阻尼控制功能，因此需要搭建可控移相器的自定义模型。现有的机电暂态程序中，PSS/E 可以实现模型的自定义，因此在该软件中搭建可控移相器的附加阻尼控制模型。本模型的附加阻尼控制传递函数搭建如图8 所示。

本模型支持移相器所在线路的过载控制，以线路有功、断面功率和母线频率为输入信号的阻尼控制。阻尼控制输出的移相角度与移相器当前（或初始）的角度相加作为最终的移相角度。

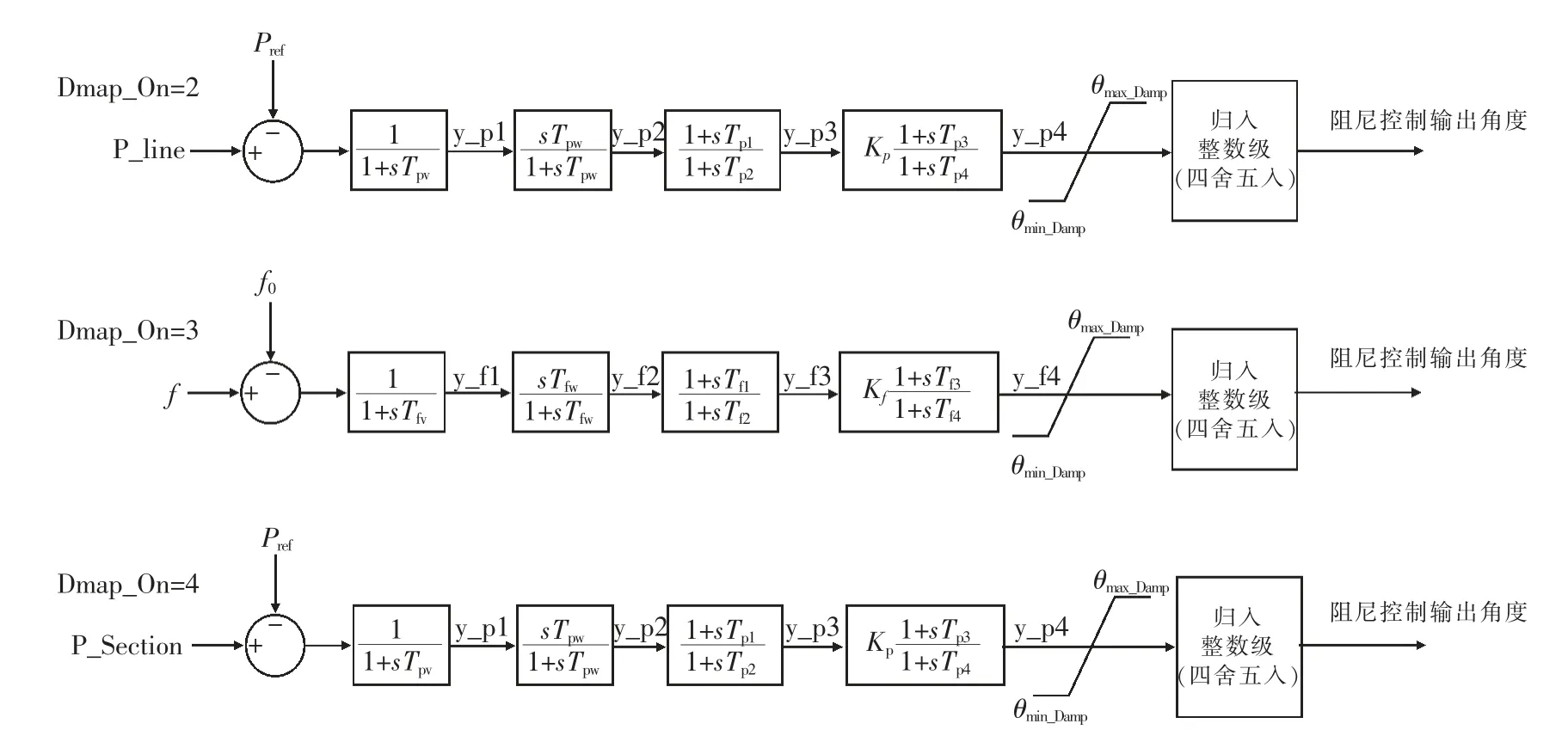
图8 PSS/E 中搭建的可控移相器阻尼控制传递函数

4.1 频率作为输入量的可控移相器参数设计

在自定义模型中，可以采用可控移相器安装线路的母线频率作为阻尼控制的输入量，在采用母线频率作为输入量时需要滤出主导的低频振荡频率，然后将采取隔直、移相、比例放大环节后输出，图9 为以频率作为输入量的可控移相器阻尼控制传递函数。

图9 以频率为输入量的传递函数

图9 中：输入f 为检测到的母线频率；Tw为隔直环节传递函数，一般可取0.02；K 为比例放大系数；T1，T2为设计的超前滞后环节时间常数；m 为超前滞后环节的阶数；θmin，θmax为移相角度的最小最大限幅值；θ 为实际输出的移相角度；T为移相的档位，可取13 档；INT（X）为四舍五入取整数档位输出到可控移相器。

4.2 功率作为输入量的可控移相器参数设计

若考虑以线路功率作为输入量，则传递函数设计简单得多，线路功率与档位调节呈现同相位或180°的反相位关系，仅需要隔直和比例放大环节即可抑制故障后引起的低频振荡问题。

图10 中的各个参数与图9 中相同，但少了超前滞后环节的设计。即使网架结构改变导致低频振荡的频率发生变化，采用功率作为输入量的阻尼设计也仍然可以抑制低频振荡。

图10 以线路功率为输入量的传递函数

5 案例分析

以华东电网2018 年夏季最大方式为例，福建电网通过1 000 kV 榕城—莲都特高压双回线和500 kV 宁德—金华双回线功率外送，如图11所示。当外送功率达到450 万kW，榕城—莲都N-2后，潮流大规模转移至宁德—金华双回线引起暂态功角电压失稳问题，考虑切除1 台600 MW 机组后，功率表现为0.256 Hz 低频振荡，振荡阻尼2.7%。按照目前对阻尼的划分，属于弱阻尼，需要继续追加切除1 台600 MW 机组后振荡阻尼才能满足在3%以上的要求。但切机不利于系统的经济运行，因此考虑在宁德—金华双回线安装可控移相器，通过可控移相器在故障后进行功率调节以提高系统的振荡阻尼水平。

图11 浙江福建联络断面

经初步分析，可控移相器的调节角度可初步设定为±5°，分别考虑以宁德站的母线频率和宁德—金华双回线路的功率作为附加阻尼控制的输入，分析各自不同输入量对抑制阻尼振荡的效果。

5.1 频率为阻尼控制输入量

若考虑以宁德站母线频率作为附加阻尼控制输入，通过相频特性分析，得到以频率作为输入量的传递函数如图12 所示。

图12 宁德—金华双线可控移相器附加阻尼控制传递函数

可控移相器的附加阻尼控制采用该传递函数进行仿真分析，在第5 s 投入阻尼控制功能。

从图13 中可以很明显看出，可控移相器投入以频率作为输入量的阻尼控制后，宁德—金华站振荡功率的幅值迅速衰减，对线路功率进行prony 分析后，得到投入阻尼控制后，阻尼比由2.7%提高到6.5%。移相器调节的角度变化曲线如图14 所示。

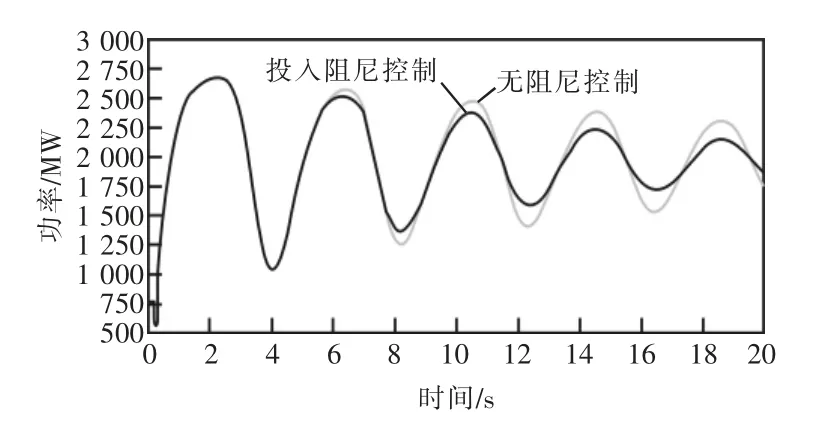
图13 频率为输入量的阻尼控制对振荡功率的影响

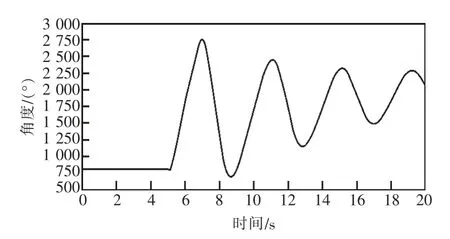
图14 投入阻尼控制后移相器角度变化曲线

采用该附加阻尼控制时，需要根据系统主动的振荡频率来设计超前滞后环节时间常数，但当网架结构改变时，电网区域间主导的振荡频率可能也会发生改变，对应超前滞后环节的时间常数也需要对应改变后才能适应新的低频振荡频率。

5.2 线路功率为阻尼控制输入量

若考虑以宁德—金华线路功率作为可控移相器附加阻尼控制输入，则阻尼控制的传递函数设计得更为简单，仅需要隔直环节，设置隔直时间常数T=0.02，比例放大环节设置的放大系数K=-0.001。该环节设计不需要超前滞后环节。因此设计的传递函数结构清晰简单，图15 为采用该输入量控制前后对改善线路故障后阻尼的效果对比。