基于小电流法的电流互感器现场测试技术
2019-12-09李航康王新燕许灵洁朱重冶
李航康,王新燕,许灵洁,陈 骁,郭 鹏,朱重冶
(1.国网浙江省电力有限公司电力科学研究院,杭州 310014;2.国网浙江德清县供电有限公司,浙江 湖州 313200;3.宁波三维电测设备有限公司,浙江 宁波 315032)
0 引言
测差法是测试电流互感器误差最常用的方法,不仅准确度高,且量值能够溯源,是电流互感器误差测量中首选的方法[1]。因此,在条件许可的情况下,应尽量选用测差法来测量电流互感器的误差。然而由于场地、电源等客观条件的限制,有时无法满足测差法所需要的条件,特别在现场测试时,由于电源限制无法提供很大的电流(2 000 A 以上),或者无法把笨重的设备(电流源、标准互感器、导线)搬运到现场,使得很难在现场用测差法对大电流互感器进行完整的误差测试,导致现场校验结果不理想,工作效率低下。针对以上情况,除了采取等安匝方法外[2],有关制造厂家研制了几种不同于测差法原理的等效测量方法,主要分为以下两大类[3-5]:
(1)低校高法
利用互感器的互易原理,即把电流互感器视为同变比的电压互感器,在电压互感器的一次侧(原电流互感器的二次侧)施加某一电压V1时,在二次侧产生二次电压,并产生误差εv,而将互感器作为电流互感器时,在其一次侧(作为电压互感器时的二次侧)施加某一电流为I1,在其二次侧产生感应电势为V1,此时电流互感器的误差εi与εv相等。采用这一原理的电流互感器校验方法通常称为低校高法[6-8]。该方法的优点是设备体积小巧,但明显的缺点是抗干扰能力差且无法进行计量传递,只能通过对有限个数的互感器进行测量后,与测差法的结果进行比对,缺乏测差法所具有的广泛有效性。
(2)负荷外推法
如果不具备在x%额定电流点测量误差的标准装置,可以通过增加二次负荷的方法间接测量,所以该方法又称负荷外推法[9-10],测量时选定的电流不小于额定电流的20%。设选定的电流百分点为m%,电流互感器的额定二次负荷为ZB,二次绕组电阻和漏电抗为Z2,分别在二次负荷ZB,电流百分点m%以及二次负荷2ZB+Z2,电流百分点0.5m%下测量电流互感器的误差,得到f1,δ1和f2,δ2。然后在二次负荷:(x/m)ZB+(x/m-1)Z2,电流百分点m%下测量电流互感器的误差,得到f3,δ3。被检电流互感器x%电流百分点下的误差按下式计算:

负荷外推法是测差法与参数测量相结合的一种方法,由于其内置的标准电流互感器、互感器校验仪、负荷箱可以得到计量传递,所以该方法得到了一些电力计量部门的认可,缺点是电子式负荷箱制造工艺复杂,故障率偏高,整机重量比低校高法的增加了不少。
本文采用的小电流法是测差法装置的一种延伸,内置的校验仪、标准电流互感器、普通电流负荷箱可以进行计量传递,过程中无需精密调节负荷箱,而且在1%以上即可工作,降低了工作电源容量,相比以上2 种方法更加适合现场的工程应用。
1 通用误差公式的推算
以上提到的3 种电流互感器误差的现场测试方法中,都借助于电流互感器误差的数学模型式(1),(2),而这一模型的基础是图1 所示的电流互感器的等效电路[11]。

图1 电流互感器等效电路
从图1 的等效电路推导电流互感器误差的计算公式为:

因为Ist为二次总电流,应有:

式中:n2/n1=N;N 为互感器实际变比。
所以:

因此:

设互感器的额定变比为SR,根据互感器误差的定义:

因为│Y(Zb+Z2)│是一个远小于“1”的量,可以把按函数展成麦克劳林级数:就是电流互感器以图1 作为等效电路的误差的级数表示法。
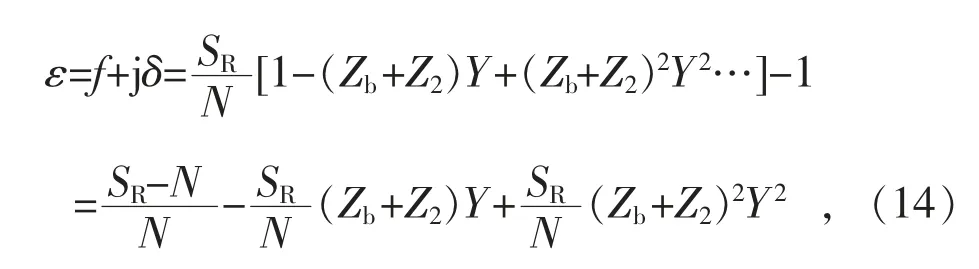
在式(14)中舍去Y(Zb+Z2)的二次及二次以上项,并在第二项中取SR/N=1,则得到:
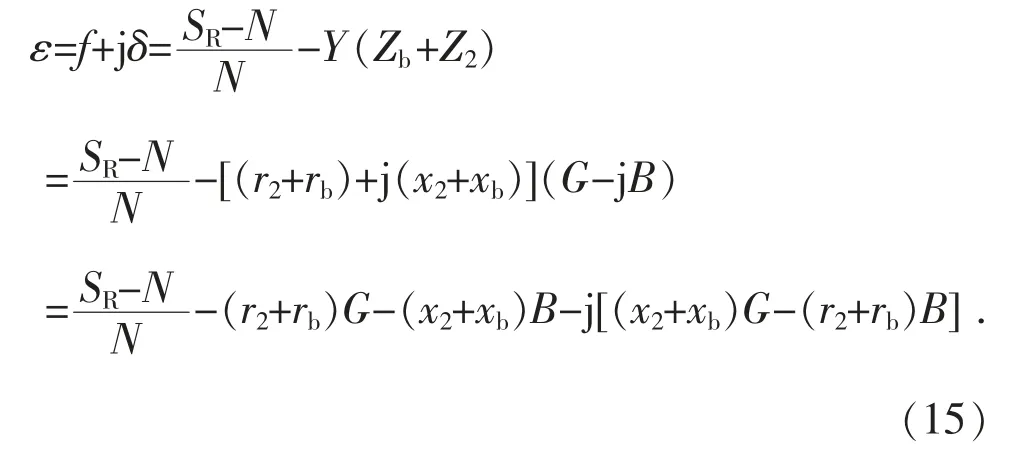
于是就得到如下通用误差公式:

2 小电流法的实施
2.1 励磁导纳的测量
在上面通用误差公式中,SR为被测互感器的额定变比,为已知数;Zb=rb+jxb为测试条件给出的二次负载,为已知数;Y=G-jB 为二次绕组的励磁导纳,可以由下述方法测得:
(1)计算二次负载电流Ict。设二次额定电流为I2n(一般I2n=5 A 或1 A),测量点的二次电流Ict与I2n之比为x%,x%为待定的工作点,已知。则Ict=x%·I2n。
(2)计算二次绕组励磁电压Vct:

式中:Z 为二次回路总阻抗。
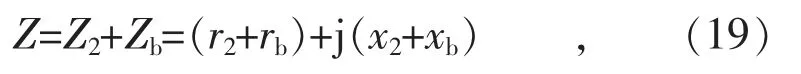
式中:rb,xb为给定的负载;r2,x2为未知数。
(3)按图2 所示测量导纳:
Yx=Gx-jBx,下标x 表示该数据为在工作电流x%·I2n时的数据。在测量G,B 的过程中可以看出:随着工作点x%的变化,二次绕组两端的励磁电压也随着变化,得出的G,B 也在变化。从实测数据可以看出,G,B 的变化对Vct的变化是非线性的,因此每一个工作点的导纳必须实测。
2.2 其他参数的测量
2.2.1 测差法及小电流法
从式(16),(17)可知,两式的右端还有r2,x2,N 为未知数,需要逐一求出。
直流电阻r2按图2 所示电路进行测量:在二次绕组中串入一测量电阻R0(阻值在0.5 Ω 左右),在一端与地之间加直流电压VD,使流过R0的电流在0.2~0.5 A 即可。则直流电阻:
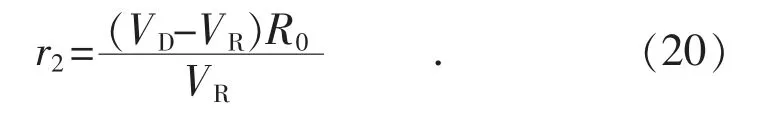

图2 导纳及电阻测量示意图
同样的接线,将直流电压改为交流电压源,可以求得各点的导纳值。
在测量过直流电阻后,互感器铁芯可能被磁化,必须进行退磁。退磁方法为:在二次绕组两端加一交流电压,一次开路。交流电压从0 V 慢慢升至20 V 左右,再慢慢降到0 V,反复进行几次即可。
N,x2的求取仍将借助测差法来解决。在较低的测量点(如20%的额定二次电流),一般的测试设备(即使在现场)还是能满足测试要求的,因此就提出了在较低的测试点用测差法,实测互感器的误差,然后再用误差的计算公式推算出大电流测试点的误差,即所谓的小电流法。
首先对式(16)进行仔细分解。在比差f 的表达式中包含3 个部分:一是(SR-N)/N 匝比误差,这对一个已绕制定型后的互感器而言是个常数,不随工作电流的变化而改变;二是二次绕组的内阻抗对比差的影响;三是二次负载对比差的影响。
后二项的影响是随着工作电流变化而变化的,原因是G,B 是随工作电流变化而变化的。因此,互感器误差随着不同工作点而变化的原因就是由G,B 引起的。
在测试设备供流能力许可的条件下,选取一测试点n0%(n0尽可能取大一些,有利于Yn0的测量,也有利于推算大电流工作点误差的准确性的提高),用测差法,实测互感器的空载误差fn0,δn0,此时式(16),(17)可写成:
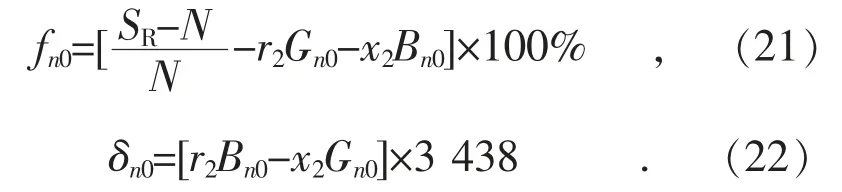
设待测点为x%,则互感器在待测点在带负载Zb=rb+jxb时的误差记为fx,δx,根据式(16),(17)有:

由式(21)—(23),式(22)—(24)得:
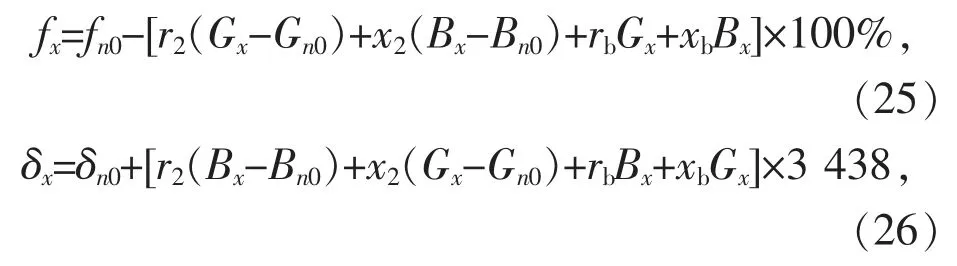
就是小电流法的数学模型。
式(25)为fx的计算公式,它包含有三部分内容:
(1)小电流实测点n0%的实测空载比差fn0,fn0中不仅包含式(21)中表达的内容,还包含了影响误差的其它因素,如分布电容等。这些因素对误差的影响在各测试点是个常数。在实测fn0时,已计入fn0中,所以在fx的表达式的其它地方不再出现,包括匝比误差(SR-N)/N。因此实际变比N 不再出现在fx的表达式中,避开了N 的求解问题。
(2)由于在n0%及x%二点励磁导纳的变化引起的比差的变化r2(Gx-Gn0)+x2(Bx-Bn0)。
(3)由负载Zb=rb+jxb对误差造成的影响:rbGx+xbBx。
现在再观察一下式(25),(26),未知参数只有二次绕组的漏抗x2了,它不仅直接影响式(25),(26)的计算,而且影响Yn0=Gn0-jBn0,Yx=Gx-jBx的测量。
直接测量或计算出x2是困难的。从表面看,在式(22)中,δn0,Gn0,Bn0,r2都已实测得到,可以直接计算获得x2,其实不然,因为在测试导纳Yn0时,下标n0表示在工作点n0%的值。
在计算确定Vctn0时,Vctn0=n0%·I2n·Z,Z 为回路总阻抗:

在空载(Zb=0)情况下,把式(25)改写成:

2.2.2 逐步副近法
对式(28)采用逐步逼近法:
(1)选取n0%,n0/2% 2 个点(n0尽可能取大些),用测差法实测互感器的空载误差,得到fn0,δn0,fn0/2,δn0/2。
(2)取x2=x2′为初始值(x2′可取0,或取x2′=r2,或其它值),

计算励磁电压:
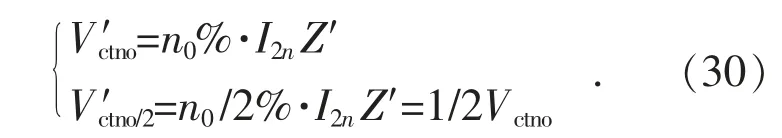
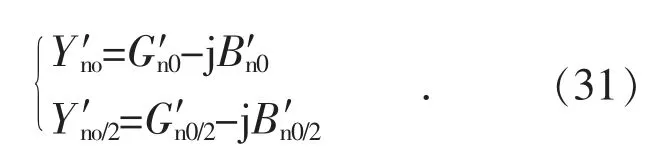
(4)将fno,fno/2,r2,代入式(28),计算得:
当然,也可以把式(26)在空载下改写成:

以式(33)为基础用逐步逼近法求解x2,2 种结果应该一致。
这里并没有证明用逐步逼近法一定会收敛,也没有讨论收敛的速度。但一般而言,只要初值选得适当,逼近过程很快能完成,如若发散,则可重设初值再试。
3 测试过程实例
下面以一个实例来说明小电流法测互感器误差的全过程。
例1:电流互感器的额定变比为1 000/5,额定容量为30 VA,cosφ=0.8,准确级为0.2 级。现有的测试设备的最大功率为750 VA,最大输出电流为600 A。
测试步骤:
(1)按图2 测二次绕组的直流电阻r2,在图中,取R0=0.5 Ω。
加电压VD=0.260 4 V,测得VR=0.155 V,计算得:
(2)取n0%=40%,n0/2%=20%,并在这2 点处用测差法测互感器的空载误差f40,f20,δ20,δ40:
f40=0.045%,δ40=2.65′;
f20=0.031%,δ20=3.25′。
(3)采用式(28),用逐步逼近法求解x2(由于过程太过冗长,故从略),求得x2=0.3,并在最后一步逼近时,测得n0%处的导纳为Y40=0.385-j1.71 mΩ。
(4)在求得x2后,即可在额定负载及下限负载下计算各测试点的励磁电压,测量励磁电流,计算励磁导纳:
计算额定负载阻抗:
计算下限负载阻抗:
计算额定负载下的二次回路总阻抗:
Z=(0.34+0.96)+j(0.3+0.72)=1.3+j1.02。
计算下限负载下的二次回路总阻抗:
Z*=(0.34+0.24)+j(0.3+0.18)=0.58+j0.48。
计算额定负载下的各测试点的励磁电压:
Vct5=5%×5×1.652 4=0.413 1 V;
Vct20=20%×5×1.652 4=1.652 4 V;
Vct100=100%×5×1.652 4=8.262 0 V;
Vct120=120%×5×1.652 4=9.914 4 V。
按图2 所示方法,在额定负载下在各测试点测试励磁导纳:G5=0.712,B5=3.015;G20=0.361,B20=1.335;G100=0.35,B100=1.124;G120=0.345,B120=1.110,单位均为mS。
计算下限负载下的各测试点的励磁电压:
(5)完成上述工作后,把上述所得数据依次代入式(25),(26)就能得出各测试点比差和角差。计算结果列于表1,为了比较小电流法的测量结果,对被测互感器用测差法在各测试点进行测试,其结果也列于表1。

表1 电流互感器误差测试数据对比
通过对比,可以看出小电流法测量与测差法结果基本一致,比差差异小于0.05%,角差差异小于2′,满足现场的使用要求。
4 小电流法的适用范围及误差控制
小电流法适用于在现场对电流互感器进行误差的测量校准,特别是现场电源容量或其他条件不满足传统测差法要求的场合。该方法主要误差来源包括起始测试电流太小造成的测试误差、漏抗测量计算出现的偏差、现场环境电磁场干扰造成的影响等。为此提出以下几点注意要点和改进措施:
(1)选取空载实测点n0%时,尽可能选n0大些(在电流源及标准互感器承受范围内)有利于空载导纳的测量。一般应使n0%尽量靠近20%。因为工作点大于20%以后,互感器的性能趋于平稳,在20%点测试合格的互感器,在100%,120%点测试一般都是合格的。
(2)一次电流源的输出容量及标准互感器的电流承受能力要选取合适:过大,会造成设备体积庞大,重量沉重,不利于现场运送和使用;过小,会限制对大电流互感器的测量。一般可选取最大被测互感器额定一次电流的20%。
(3)在求解x2过程中,有时因工作点低(二次电流小),二次绕组阻值小,使得计算出的二次励磁电压很低,影响励磁导纳的准确测量,从而影响x2的测量准确度。此时,可在二次回路中串接一电阻r0,来提高二次励磁电压。r0的值并入r2,使r2′=r2+r0。当然,在逼近x2过程中测得的励磁导纳不再是空载时的导纳,不能在式(25)、(26)中直接使用。
(4)仪器可在导纳测量和误差测量环节引入异频测量的概念,在45 Hz 和55 Hz 2 种工作频率下测得的结果平均后代替50 Hz 情况下的数据,以消除现场电磁场环境影响带来的测量误差[12]。
5 结语
当精度要求达到0.05S 级,采用小电流法的电流互感器现场测试仪将在电力部门有着广泛的应用。为了满足便于携带的需要,通常将电子源、校验仪、负荷箱、标准电流互感器、控制器等集中安装在一个机箱内,这样的源功率通常在3~4 kVA 左右,配合合适的大电流导线,使装置输出10%以上的额定电流,基本上能够满足220 kV,5 000 A 及以下的电流互感器现场测试的需求,相比于传统的测差法升流装置,要在220 kV 的高度上输出5 000 A 的电流,需要的电源容量将在100 kVA 以上[13-14],考虑到设备和现场电源的限制,小电流法装置带来的便利是很明显的,同时由于采用了普通的自动电流负荷箱,使得装置在计量方面也有相当好的可溯源性,如果需要测量具有较长管道的GIS 电流互感器[15-16],可以将装置的电子源部分与其他部分分离,这样只要适当提高源的容量,使得对现场电流互感器的适应能力接近理想,测试对象除了GIS,也可以包括电流达到数万安培的发电机出口的电流互感器[17]。
