含可破碎填料的填石路基压实仿真
2019-12-09丁智勇李国政张通化徐信芯
丁智勇,李国政,张通化,徐信芯
(1.长安大学 道路施工技术与装备教育部重点实验室,陕西 西安 710064;2.东风康明斯发动机有限公司,湖北 襄阳 441000)
0 引 言
填石路基可将开凿路堑、爆破隧道及开采矿山时产生的弃石重新利用,起到保护水文、农田,改善当地环境的作用,具有社会和经济双层效益[1]。国内学者对填石路基的施工做了一些研究,但施工技术仍处于探索过程中。随着计算机技术的发展,相应的模拟软件随之出现。Saussine等通过完全接触动力学,对多边形颗粒材料在重复荷载作用下的沉降状况进行了模拟,结果表明了离散元法在解决材料沉降问题上的可行性[2];Karrech建立三维离散元模型,研究了循环载荷下粒料的行为,表明通过优化计算过程可以将颗粒的流动计算时间减少[3];涂帅选用Hertz-Mindlin模型,仿真分析高性能级配碎石的应力、应变特性,探究级配型碎石密实过程中的自锁条件,并建立了相应的多尺度关联法[4];王团结利用PFC三维离散元软件,研究了土石混合料细观与宏观参数对压实效果的影响,提出以孔隙率作为土石混合料离散元模型压实效果的评价指标[5];方磊在考虑颗粒单元之间接触性质的基础上,采用随机离散元法分析了激振力、频率对压实度的影响[6];黄宝涛使用二维离散元法,探究了路基填料在振动压实下,空间组构、力学特性的演变过程[7];王建通过三维离散元软件,分析了非弹性颗粒在循环载荷作用下的瞬态变化,对碎石材料在振动作用力下的运动规律进行研究[8]。
离散元数值模拟是模拟碎石块体等土结构压实的一种有效方法,但在模型建立方面存在一些不足,如:在对土颗粒建模时都是以球形为单元,与现实颗粒形状不符;在数值分析中,忽略颗粒破碎的影响,不能很好地反映实际压实情况,仿真误差大。本文基于EDEM软件对大粒径、复杂形状且可破碎颗粒进行压实仿真,反映填石路基的压实性质。
1 颗粒模型的建立
1.1 刚性颗粒生成
石料爆破开采后,通过5~20 mm筛孔的石料占10%,此外50~200 mm的颗粒占60%,由于压路机压实作用范围有限,因此文中岩石颗粒粒径范围为5~160 mm,建立扁平状和棱锥状颗粒模型,如图1所示。填料各粒径分布占比为正态分布[9-10],如图2所示。岩性为石灰岩,参数[11]见表1。

图1 不同形状颗粒

图2 粒径分布
1.2 可破碎颗粒生成
为真实地反映填石路基的碾压特性,建立可破碎颗粒模型。通过EDEM 应用程序编程接口,编译

表1 石灰岩参数
生成颗粒替代插件,供EDEM软件调用,并以此生成可破碎颗粒模型。利用EDEM颗粒工厂生成若干大粒径颗粒,通过颗粒黏结插件把小颗粒粘接在一起,形成具有一定强度和形状的岩石颗粒,替代原来的大粒径颗粒,示意如图3所示。其岩石强度通过小颗粒间的黏结力值表示,其破碎遵循莫尔强度理论,计算公式为
式中:τ为最大切应力;σ为最大正应力;Kn为正向刚度系数;Kt为切向刚度系数;V为泊松比;E为岩石弹性模量;r为Friction小颗粒半径。
图3 颗粒替代示意
本文中Friction小颗粒半径为5 mm,将颗粒参数代入式(1)~(3)得τ=1.01×108N·m-2、Kn=4.16×109N·m-3、Kt=2.08×109N·m-3。
2 填石路基模型
根据文献[5]及相关规范,路基尺寸设置为1.60 m×0.9 m×0.72 m,铺层厚度控制在0.6 m左右。采用上面已建立的非球形刚性颗粒和可破碎颗粒对路基填充,可破碎颗粒选用Hertz-Mindlin with Bonding本构模型。填石路基各碎石填料颗粒混合后,碾压选用Hertz-Mindlin 接触本构,参数为软件本构模型的配置参数,填料组成如表2所示。基本接触参数(恢复系数、静摩擦系数、滚动摩擦系数)需进行“虚拟试验”标定,标定方式采用堆积角试验,通过正交组合,设定包括标准文件在内的10组组合数据,最后得到接触参数,如表3所示。数值模型采用三维离散元软件EDEM建立,将振动轮与路基接触面作条形处理。模型为长方体有侧限,在顶面分别建立颗粒工厂,生成填料和加载板墙体单元,如图4所示。填料平衡静止后,进行预压整平及后续振动荷载的施加。
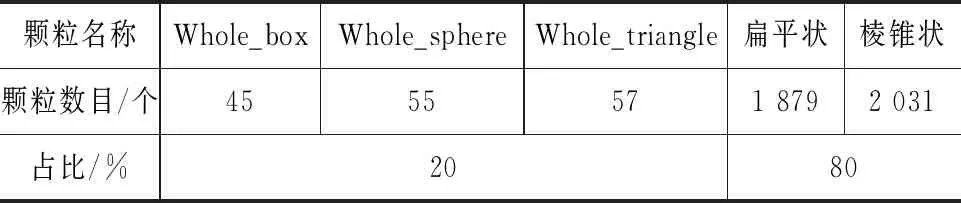
表2 填料组成

表3 接触参数

图4 路基模型示意
由于在离散元软件中不能给墙体单元直接施加荷载,只能施加位移,控制加载速度,以达到加载的效果。根据能量等价公式[12-15],P0=F(t)v(t),即v(t)=P0/F(t),因此文中通过控制墙体单元加载速度,实现振动荷载加载。
3 模拟过程及结果
3.1 压实过程模拟
首先,按照正态分布和填料组成情况生成仿真颗粒,并在载荷施加前确保颗粒达到重力平衡态。通过控制加载板将平衡后突起的填料整平,确保后期加载均匀,以防“逃逸”,最后通过Geometry Bin功能创建检测区,控制加载板,改变相应参数,先静压2遍,后循环振动碾压。碾压模拟情况如图5、6所示。

图5 碾压2遍

图6 碾压6遍
3.2 振动频率影响效应分析
激振力设定为200 kN,记录振动频率为28、35、48 Hz时的路基压实状况,振动频率对孔隙率的影响如图7所示。
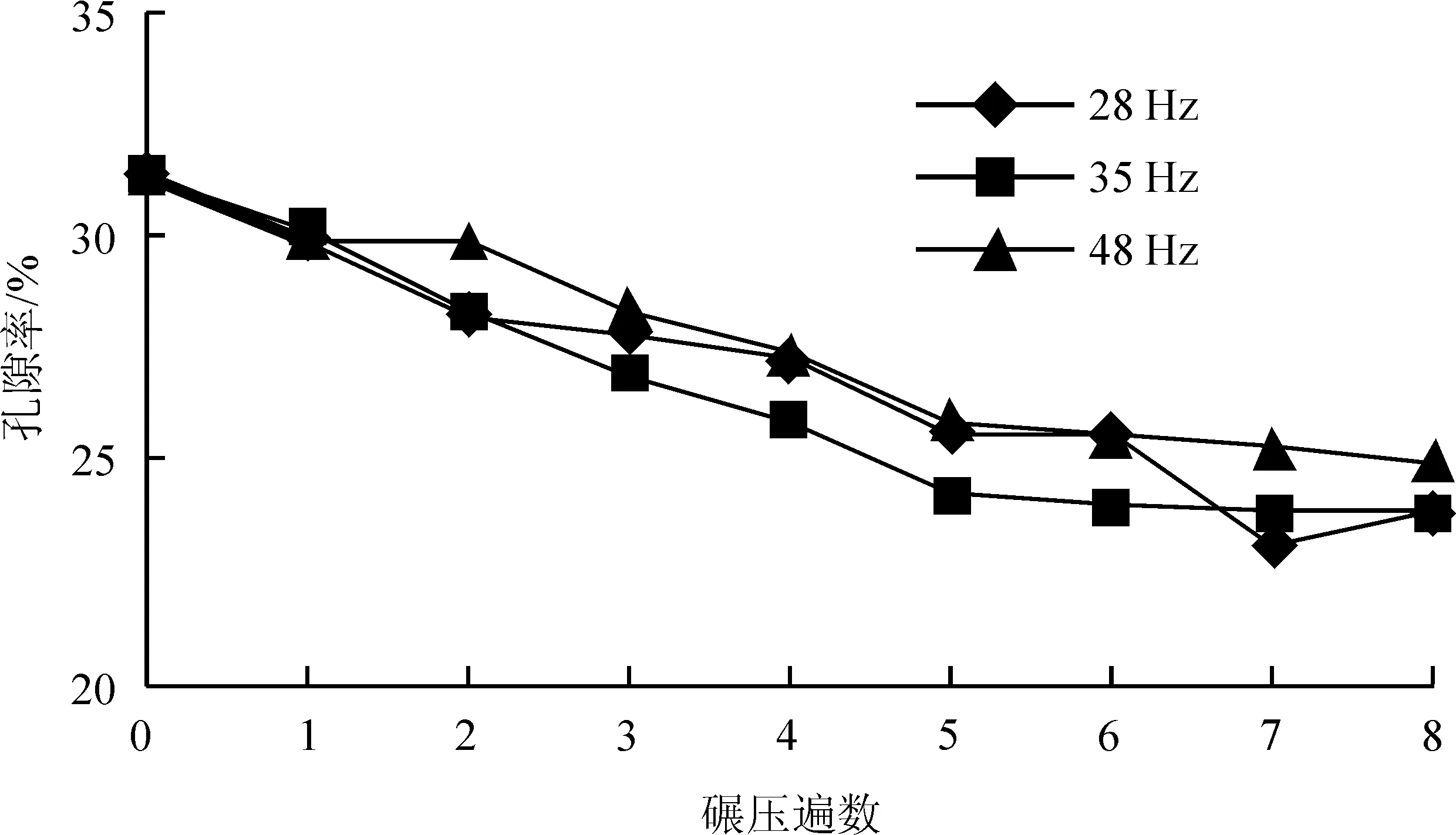
图7 振动频率对孔隙率的影响
从图7中可以看出,振动频率对最终的压实效果有影响。振动频率为35 Hz时,碾压后孔隙率最低;振动频率为48 Hz时,压实程度相比最低,可见振动频率并非越高越易压实。观察图7可以看出:随碾压遍数增多,孔隙率降低,碾压6遍左右,孔隙率基本稳定在一定范围,变化幅度较小;路基在实际碾压中,若激振力参数不变,碾压6遍左右基本已达到最佳压实效果,再增加碾压遍数的工程意义不大。
3.3 激振力影响效应分析
振动频率设定为35 Hz,记录模拟激振力200、270、340 kN下路基压实状况,结果如图8所示。由图8可知:激振力越大,最终孔隙率越小,但不同激振力之间最终孔隙率之差相比不同频率最终孔隙率之差小。可见,频率对压实效果影响较大。从图8可以看出:频率一定,不同激振力下,随碾压遍数的增加,密实度提高;碾压超过5遍,孔隙率变化减小;在激振力为270、340 kN的情况下,碾压超过6遍后,孔隙率出现轻微反弹,路基上层可能出现填料松散、过压实的情况;对比激振力200 kN和270 kN,其路基压实效果相差不大,对比激振力270 kN和340 kN,大激振力下路基更密实。
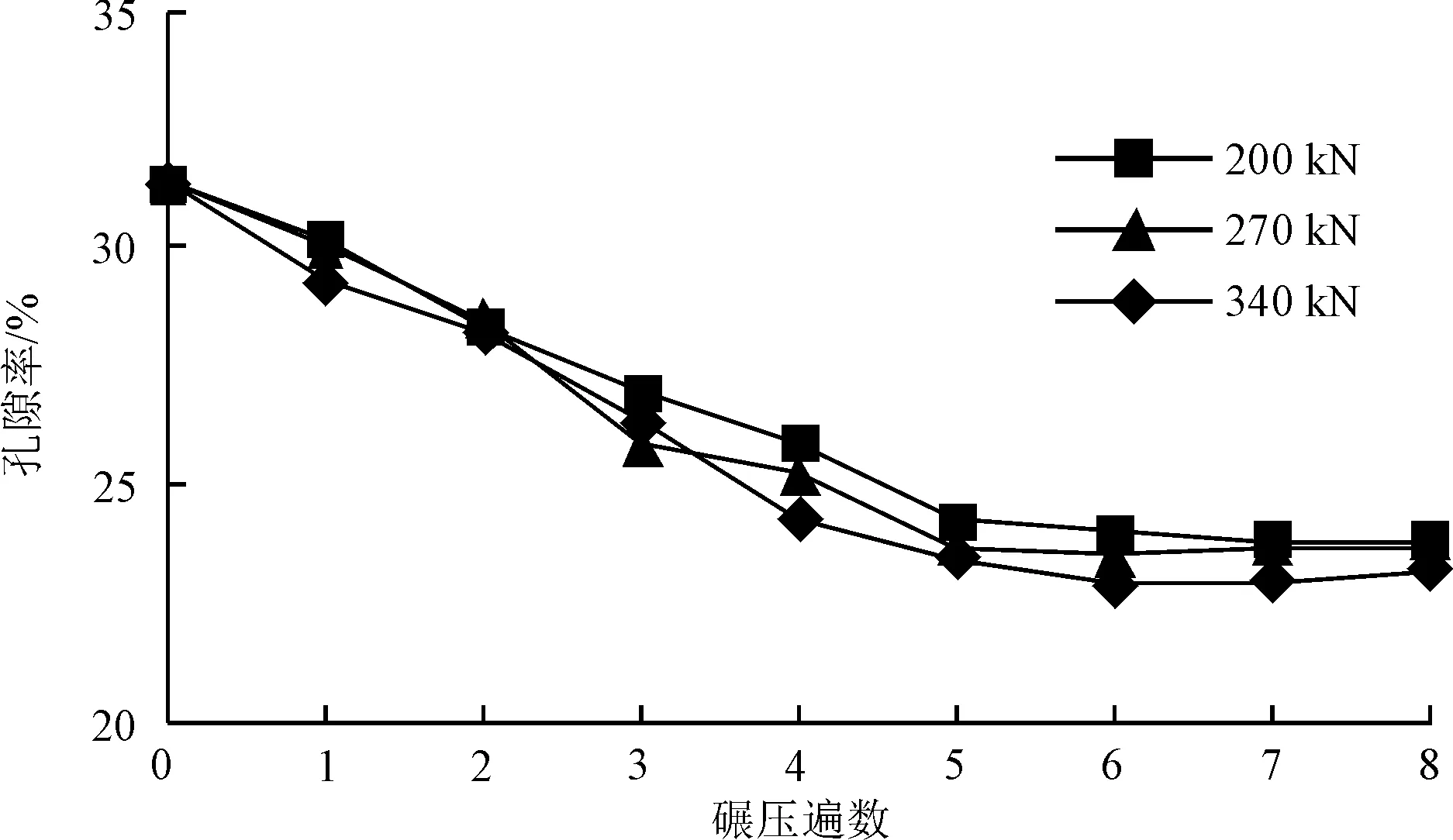
图8 激振力对孔隙率的影响
3.4 颗粒破碎过程分析
利用EDEM自带的对颗粒黏结键断裂统计功能,将断裂总键数与生成总键数之比作为破碎率的量化指标。颗粒黏结键共生成106 110个,为了分析颗粒破碎过程,选用(0,1,0)切面作为示意面,对隐藏扁平状和棱锥状颗粒,只显示大颗粒的内部黏结键,35 Hz、200 kN下填料破碎率与碾压遍数关系如表4、图9所示,破碎过程如图10所示。
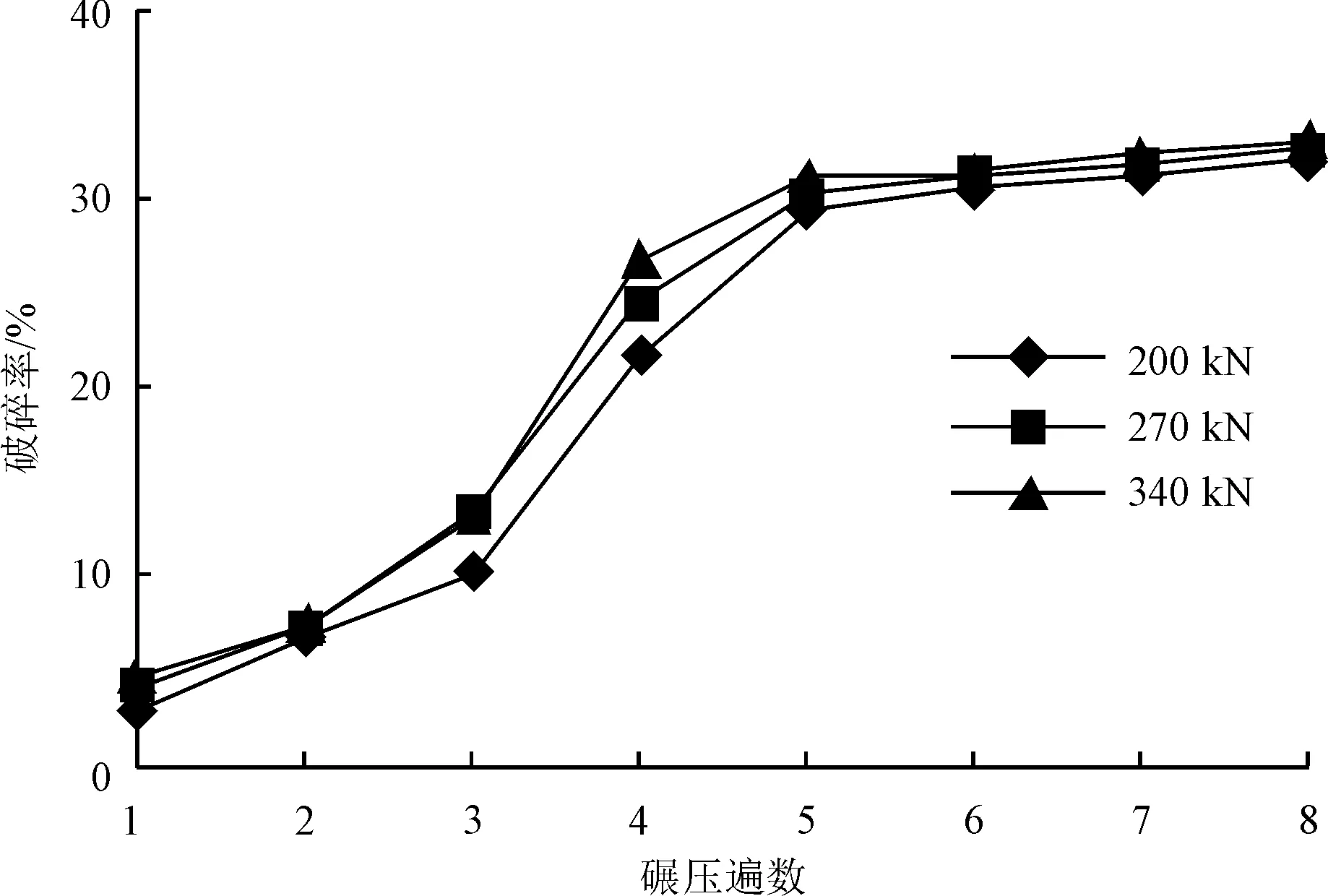
图9 破碎率与碾压遍数关系曲线

图10 颗粒破碎分布

碾压遍数200 kN破碎率/%270 kN破碎率/%340 kN破碎率/%平均破碎率/%12.94.24.73.9326.87.37.57.20310.213.413.212.27421.724.526.824.33529.430.231.230.27630.531.331.531.10731.231.832.331.77832.032.633.132.56
对比不同遍数下的颗粒破碎分布可以看出:颗粒的破碎主要集中在铺层上部,越接近振动源,破碎越明显。正方体、三棱柱、球体3种颗粒,以棱柱形颗粒破碎最多。对比分析3种颗粒体积,棱柱形的体积为554 093 mm3,球体颗粒体积为523 333 mm3,正方体颗粒体积为224 286 mm3,棱柱形的体积最大,其受到的总合力最大,并且棱角较多的颗粒应力分布不均,易断裂。
结合图9、10和表4可看出:颗粒碾压1遍,平均破碎率为3.93%,说明破碎率低,颗粒堆积松散,颗粒以下移运动为主;碾压2、3遍,断裂键数量增多,破碎率提高至12.27%,颗粒变形较大,部分颗粒发生破损;碾压4~5遍,平均破碎率达到30.27%,在当前设定的碾压参数下,颗粒破碎基本完成;碾压6~8遍,破碎减缓,破碎率只增加了2.29%。由此可将颗粒破碎过程整体分为四大阶段,即运动阶段、变形阶段、破损阶段、稳定阶段。
4 试验验证
为验证仿真的可靠性,参考文献[15]的现场压实试验结果,即:碎石填料为隧道爆破产生的弃渣;路基松铺厚度控制在50 cm,选用YZ20J-3型振动压路机,参数见表5,碾压方式为先静压1遍、再微振1遍、后强振3遍;现场铺设厚度为0.2 mm的聚乙烯塑料薄膜,采用灌水法检测孔隙率,每20 m作为1个断面,共设9个测点,数据如表6所示。
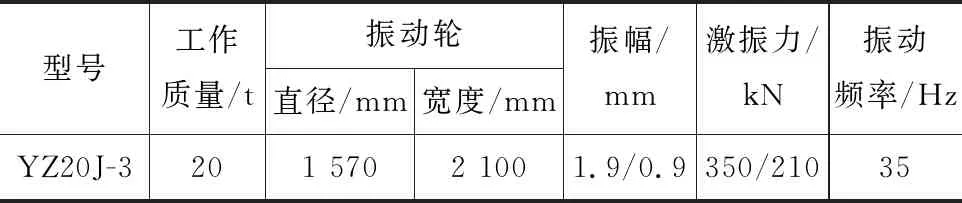
表5 振动压路机参数
由表6可知,参考文献的路基松铺后,均值在29.42%,仿真填料初始生成的孔隙率为31.36%,两者相差1.94%。主要原因是:实际松铺中,由于有推土机进行摊铺、平地机进行整平,相当于进行了预压;现场碾压完成后孔隙率平均值为22.55%,仿真中填料在碾压6遍后的孔隙率平均值为23.44%,相差仅为0.89%;现场实际碾压后孔隙率平均降低6.22%,仿真模拟的孔隙率平均降低7.92%,两者相差1.7%。可见模拟结果与实测值非常接近,孔隙率变化趋势如图11所示。
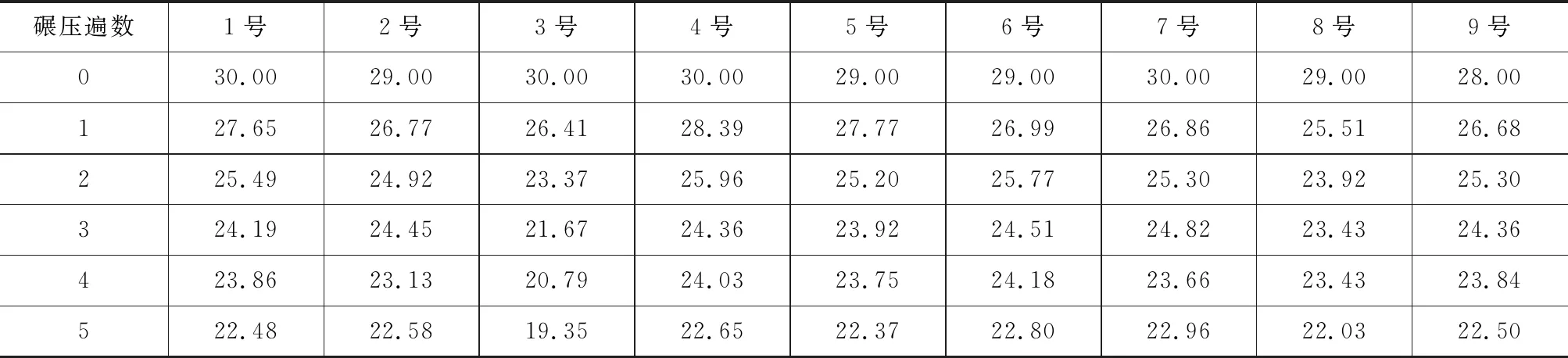
表6 孔隙率现场试验结果 %
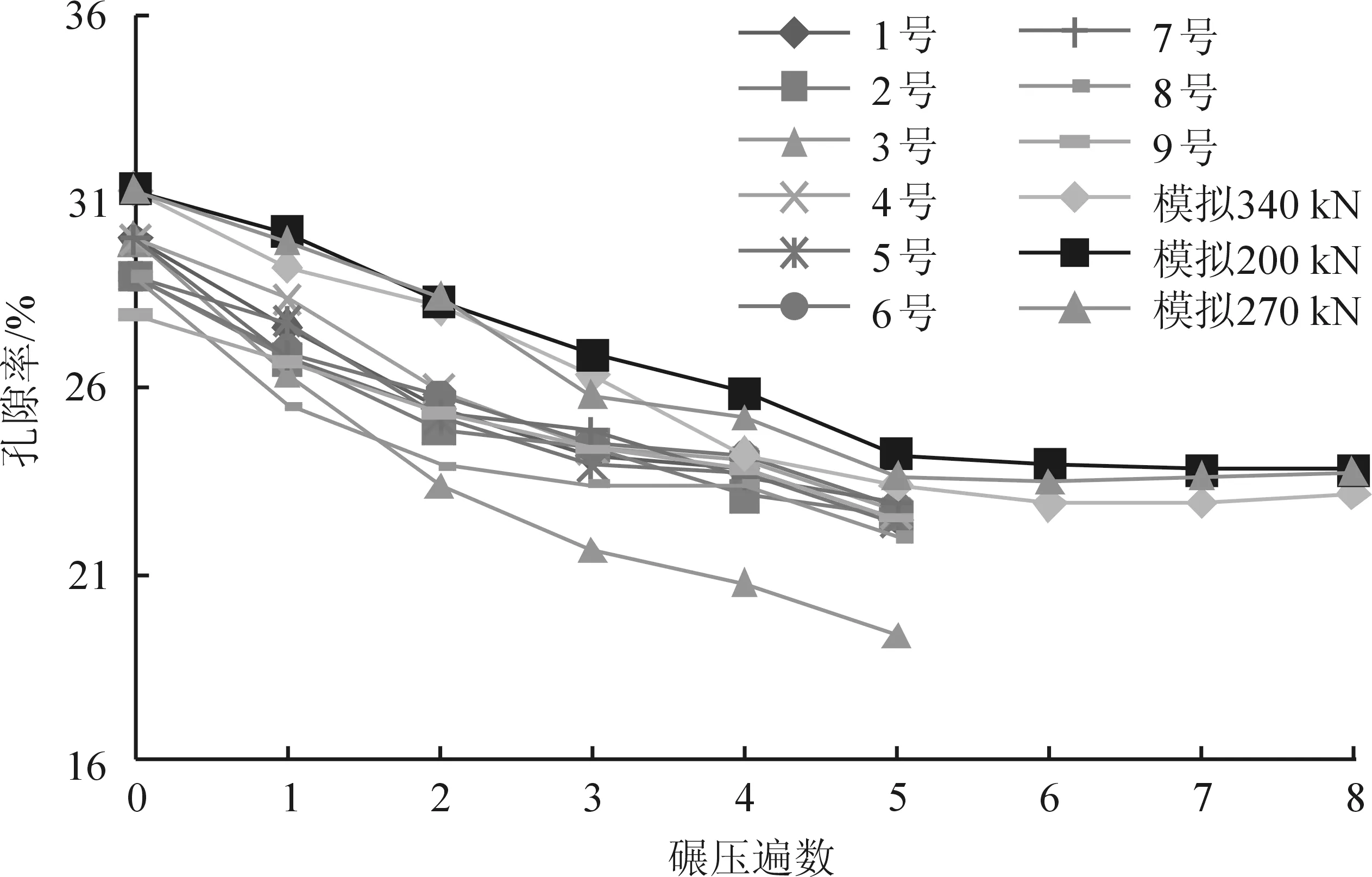
图11 孔隙率参考数据与仿真结果对比
从图12中可以看出,模拟所得路基压实孔隙率变化趋势与参考实测孔隙率变化趋势相同。孔隙率在碾压前3遍变化幅度较大,碾压第4、5遍,孔隙率趋向稳定,变化不大。
5 结 语
(1)振动频率过高或过低都不利于路基密实,仿真得出35 Hz振频下密实效果最佳。激振力大可以更好地促进颗粒的流动和密实,获得更好的压实效果。碾压遍数对设备做功的有效利用非常关键,路基碾压过程中,压实遍数控制在5、6遍最佳。
(2)路基压实过程中颗粒整体可分为运动、变形、破损、稳定四大阶段;填石颗粒破碎集中在蹍压过程的第4、5遍;在压实过程中,不同形状的颗粒破损情况不同,同等岩石强度下,棱角多、体积大的颗粒破损最大。
(3)通过比较仿真模型与参考文献的实测孔隙率发现,仿真初始孔隙率与实际仅相差1.94%,碾压后孔隙率仅相差0.89%,孔隙率降低量平均相差1.7%,且两者孔隙率整体变化趋势相同,证明用可破碎颗粒的压实离散元法模拟填石路基压实过程具有可行性。
