三相电动机的动态特性分析

2019-12-06

防爆电机 2019年6期

(万高(南通)电机制造有限公司，江苏南通 226015)

0 引言

采用直接法起动三相电动机，所需设备少、成本低且方法简单。但采用此种方法频繁起停电动机会对电动机的使用寿命产生影响[1]。因此分析电动机的起动过程，并准确计算出电动机的动态特性曲线对电动机的选型与设计有着极其重要的意义。

采用稳态法对电动机的起动过程进行分析虽然简单可行，但无法准确描绘出整个起动过程中电动机的状态[2]。在一些对电动机起动容量及起动时间有限制的工况下，则需要利用动态理论来分析电动机起动过程。以ABC坐标系为基础，建立电动机起动过程的动态方程组，通过对此动态方程组的求解，便可到动态理论下电动机的机械特性曲线。根据得出的机械特性曲线及拟合后的负载曲线即可精确求得电动机到达稳态运行时的时间。

1 三相电动机动态方程组

三相电动机从初始零转速加速到额定转速的过程中，其动态方程组为一变系数非线性微分方程组[3]。在建立电动机的动态方程前，先要将绕组中的电流定义为动态变量最后通过数值法求解[4]。以ABC坐标系为基础建立出的电动机动态方程组，便于依据电流值对计算结果进行检测与核对。根据ABC坐标系下定转子三相绕组在空间与相位上的关系可建立如下的状态方程组[5]

(1)

式中，u、i—电机的电压和电流矩阵；us、is—定子绕组的端电压及电流矩阵；ur、ir—转子绕组的端电压及电流矩阵；R、L—电机的电阻及电感矩阵；Rs、Rr—定子和转子绕组的电阻矩阵；Ls、LR—定子和转子绕组自感矩阵；Msr、Mrs—定子和转子绕组互感矩阵；θ—定转子绕组之间的夹角；Ω—电机的角速度；P0—电机的极对数；J—总转动惯量；RΩ—电机的旋转阻力系数；TL—负载转矩。

根据牛顿第二定律，可得出旋转运动系统的转动方程式

(2)

式中，Te—电动机的电磁转矩。

ABC坐标系下的电动机电磁转矩方程[6]可表示为

(3)

式(1)、式(2)、式(3)组成了以ABC坐标系为基础，建立的电动机起动过程动态方程组。

3 三相电动机起动过程的分析

三相电机起动时，其转子电流值远大于额定状态下的电流值，使得电动机定转子铁心出现过饱和的现象。此外，起动过程中电动机的转速又是时变的。所以在对电动机的起动过程进行分析时必须对电动机转子的各物理量进行校正[7]，其校正公式可表示为

(4)

式中，Rrs、Rrn—起动时和额定运行时转子绕组电阻；Xrs、Xrn—动态和稳态时刻电动机转子的绕组漏电抗；s、sn—电动机动态和稳态运转时的转差率。

三相电动机将负载从零转速加速到稳态工作转速的过程中，由于转速的时变性，故式(1)即为一变系数非线性方程组。通常可通过数值法对其进行求解。设电动机转速零时刻为t0，此时电动机定转子电流为is(t0)=0，ir(t0)=0。根据给定的初始值并结合数值法对电动机的动态方程组进行求解，直至电动机到达稳态运行状态为止。此外根据电动机达到稳态时的计算次数以及时间步长可求出电动机的起动时间t=nh。采用此种方法时，时间步长h取值越小计算精度越高，但计算量会大大增加。实际计算表明，对于三相电动机，时间步长取0.0003s到0.0005s比较合适。

4 计算结果及分析

以一台1000kW、2极、50Hz电机为例，根据上述三相电动机动态特性方程组并结合数值法对此电动机的动态机械特性以及起动时间进行解析计算。计算前需将表1给出的负载参数进行拟合以便准确求得电动机的起动时间。图1、图2分别为稳态理论和动态理论下得出的机械特性曲线。

表1 负载转速与转矩关系

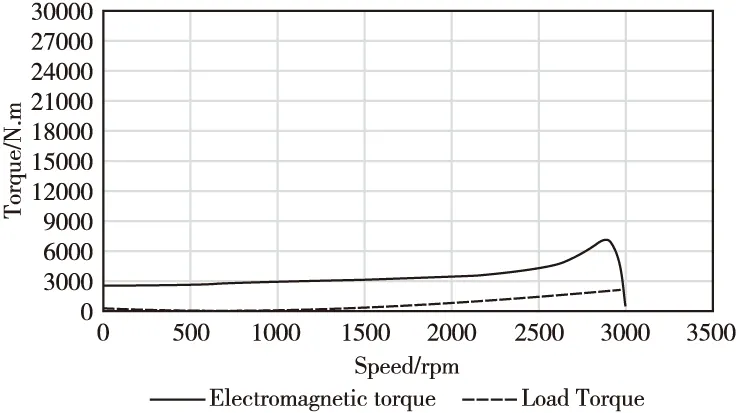
图1 稳态机械特性曲线

图2 动态机械特性曲线

分析计算出的稳态和动态机械特性曲线可以了解到，稳态特性曲线和动态特性曲线总的变化趋势是相似的。但在初始时刻定子绕组电流中既有基频交变分量又有非周期低频交变分量。此非周期低频交变分量会与转子电流会产生一静止的磁场，此静止磁场与基波磁场相互作用产生交变的电磁转矩，因此在电动机起动初期动态特性曲线电磁转矩中包含很强的脉振分量[8]。采用稳态法计算电动机的机械特性曲线时则无法表述这一现象。在起动中期，随着电流中非周期性分量的消失，稳态特性曲线和动态特性曲线中的电磁转矩值几乎是相同的。当转速到达到临界转速附近时，稳态特性曲线中的电磁转矩将会稍大于动态特性曲线中的电磁转矩。试验表明，电动机的实际起动时间更接近于用动态法求出的起动时间，这说明了动态理论在分析电动机起动过程及起动时间时的准确性。