AlxIn1-xAs电子结构和光学性质的第一性原理研究
2019-12-06张振东黄延彬李志宏罗子江
张振东, 王 一, 黄延彬 , 李志宏,杨 晨, 罗子江, 郭 祥, 丁 召
(1. 贵州大学大数据与信息工程学院, 贵阳 550025; 2. 贵州财经大学信息学院, 贵阳 550025;3. 半导体功率器件可靠性教育部工程研究中心, 贵阳 550025; 4. 贵州省微纳电子与软件技术重点实验室, 贵阳 550025)
1 引 言
近几十年来,III-V族化合物半导体材料获得了广泛关注及研究[1]. 其中,InAs材料因其高电子迁移率(33000 cm2/V s)及窄带隙(0.36 eV)等性质,在等离子体滤波器、光电集成、高速/高频器件及太阳能光伏器件领域应用广泛[2]. 然而,由于InAs衬底的制造成本高且重复率低,因此在成本较低的衬底(如GaAs)上生长InAs层成为更好的选择,而为了解决InAs与GaAs高达7.2%的晶格失配量,在两者间生长缓冲层就很有必要[3]. 目前,生长AlInAs缓冲层的工艺已很成熟[4],其能确保良好的绝缘性能. 此外,Solov’ev等人[5]对AlxIn1-xAs缓冲层的设计及MBE生长条件进行了研究,通过变化组分(x范围为0.17-0.95)以改善其表面结构的形态特征. Loke等人[6]研究了生长温度对AlxIn1-xAs(x范围为0.79-0.95)缓冲层表面形貌的影响. Sorokin等人[7]研究了不同组分AlxIn1-xAs(x范围为0.21-0.95)缓冲层下,In0.75Ga0.25As/AlInAs量子阱结构的应变弛豫机制. Kujofsa等人[8]比较了各组分下AlxIn1-xAs及InxGa1-xAs两种材料体系的平衡弛豫情况. 然而,当前关于AlxIn1-xAs材料光电性质的系统研究还很少,本文将对各组分AlxIn1-xAs的晶体结构,电子结构和光学性质进行计算,并对其各项性质随组分变化的趋势进行研究,为AlxIn1-xAs材料在实际中的应用提供一定的理论依据.
2 计算模型和方法
2.1 晶体模型
本文采用16个原子的2×1×1超胞作为计算的对象,如图1为InAs的晶体模型,在此基础上,利用Al原子替换不同数量的In原子可以得到不同组分的AlxIn1-xAs(x=0,0.125,0.25,0.375,0.5,0.625,0.75,0.875,1)晶体. 然而,一些组分的AlxIn1-xAs模型种类众多,若将其尽数计算将会是巨大的工作量,考虑到在研究各种组分对材料性质的影响时,可以忽略对称类型的因素[9],因此,对各组分AlxIn1-xAs晶体我们将只选取一种模型进行计算,选取模型的对称群属分别为:F-43M(InAs /AlAs)、P-42M(Al0.125In0.875As /Al0.875In0.125As)、P2221(Al0.25In0.75As /Al0.75In0.25As)、P222(Al0.375In0.625As /Al0.625In0.375As)以及P2(Al0.5In0.5As).

图1 InAs超胞模型Fig. 1 Supercell for calculation of InAs
2.2 计算方法
本文中的计算将在Materials Studio软件的CASTEP模块下进行,交换关联势选择LDA +U和CA-PZ.U值选取在As-4p上,设置值为2.75 eV. 在结构优化设置中,设定自洽精度为5.0×10-6eV,原子最大相互作用力为0.01 eV/Å,原子最大位移为5.0×10-4Å,最大内应力为0.02 GPa. 此外,设置平面波截断能Ecut为450 eV,取k网格的大小为2×4×4. 此外,本文研究的几种元素的价电子组态为:Al(3s23p1),In(5s24d105p1),As(4s23d104p3).
3 计算结果与讨论
3.1 晶体结构
3.1.1驰豫情况
建立各组分模型时,引入的Al原子将打破原InAs晶体结构的平衡,为获得准确的晶体结构,须先对各模型进行结构优化. 优化结果显示,Al原子的引入将使晶格结构发生畸变[10],不同组分晶体的键长键角将会发生不同程度的变化,本文对此进行了统计,定义驰豫度R[11]为
(1)
式中Oa表示晶体优化前的参数,即原本InAs晶体的参数,Ob则表示晶体优化后的参数.R为正值表示优化后的参数增大;R为负值则表明优化后参数减小;优化前后参数不变则R为0. 表1统计了不同组分下AlxIn1-xAs晶体的In-As键、Al-As键、Al-As-Al键角及In-As-In键角的驰豫度,由此可以获得各体系原子结构的变化情况.
数据显示,随Al原子引入而新形成的Al-As键比原本结构的In-As键更短,这主要归因于Al的原子半径相对In原子更小,因此同样与As原子成键时的键长更短;同样,In-As键也会略微缩短,随着Al组分的增加,缩短幅度加大;新形成的Al-As-Al键角相较原本结构的In-As-In键角更大,且在Al组分为0.75时达到最大值,此后增大幅度迅速回落直至恢复原本大小;此外,In-As-In键角将减小,减小的幅度同样在Al组分为0.75时达到最大.
表1 不同Al组分下各参数的驰豫度
Table 1 Variation of the relaxation degree of each parameter with different aluminium proportions
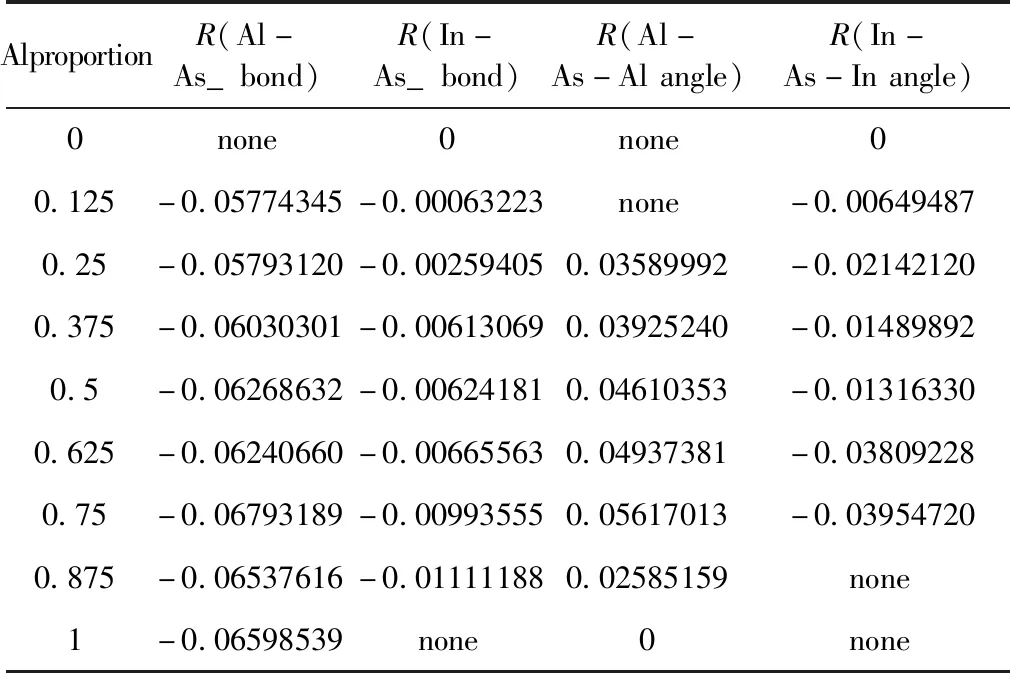
AlproportionR(Al-As_bond)R(In-As_bond)R(Al-As-Alangle)R(In-As-Inangle)0none0none00.125-0.05774345-0.00063223none-0.006494870.25-0.05793120-0.002594050.03589992-0.021421200.375-0.06030301-0.006130690.03925240-0.014898920.5-0.06268632-0.006241810.04610353-0.013163300.625-0.06240660-0.006655630.04937381-0.038092280.75-0.06793189-0.009935550.05617013-0.039547200.875-0.06537616-0.011111880.02585159none1-0.06598539none0none
3.1.2晶格常数与晶胞体积
温度为300 K时,InAs与AlAs的晶格常数分别为6.0583 Å和5.66139 Å[12],与二者的实验值相比,本文计算误差仅为0.51%和0.56%,这表明计算参数设置合理,计算精准度较高. 不同组分下AlxIn1-xAs晶体的晶格常数变化规律可由Vegard定律总结[13],如式(2)所示,其中x为Al原子的组分:
aAlxIn1-xAs=x·aAlAs+(1-x)·aInAs
(2)
Vegard定律是一个近似的经验法则,其认为在恒定的温度下,物质的晶格常数与其组分元素的浓度存在线性关系. 图2(a)展示了AlxIn1-xAs晶格常数随Al组分由0至1变化的情况.
其中红色实线(Vegard)表示满足Vegard定律的晶格常数变化曲线,而蓝色虚线(Caculation)则表示计算结果的变化曲线. 图2(a)显示,计算得到的晶格常数的变化趋势基本符合Vegard定律,只是在组分x为0.25-0.75范围时,计算值略小于理论值. 其原因可能为这几种组分下的AlxIn1-xAs晶体中Al和In原子数量相当,晶格失配现象较为凸显,因此软件在结构优化时产生了误差.
此外,图2(b)显示AlxIn1-xAs的晶胞体积随Al组分的增加将迅速减小,这是由于AlxIn1-xAs晶体α、β和γ角均呈90度,其体积与晶格常数的三次方呈线性关系造成的.
3.2 电子结构
3.2.1能带结构
对模型进行结构优化后,对各组分AlxIn1-xAs晶体的能带结构进行了计算,图3展示为其中四种组分的AlxIn1-xAs晶体能带情况.
图3(a)为InAs晶体的能带图,其为直接带隙结构,由图4展示的分波态密度可知,其价带最顶峰的能态源于In和As原子P轨道的贡献,而导带最底峰的能态则由In和As原子的S、P轨道共同贡献. 此外,图3(b)、(c)、(d)分别展示了Al0.25In0.75As、Al0.5In0.5As、Al0.75In0.25As等三种组分的晶体能带结构,随着Al组分增加,AlxIn1-xAs晶体不仅产生了新的能带,且带隙值不断增大. 图3(b)显示Al0.25In0.75As的能带依旧具有直接带隙结构,此时Al组分较少,InAs仍占据Al0.25In0.75As晶体主导地位,因此导带的最低点和价带的最高点均位于Gamma点;而当Al组分超过0.5时,AlAs将逐渐占据主导地位,导带最低点有从Gamma点位置转移到高对称点R位置的趋势,能带也将逐渐转变为间接带隙结构. 本文计算的各组能带结构与实验结果吻合良好[14].
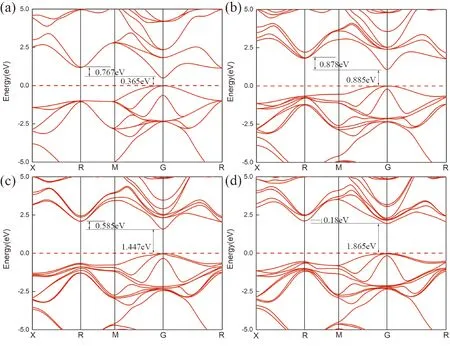
图3 AlxIn1-xAs体系能带结构Fig 3 Band structure of AlxIn1-xAs
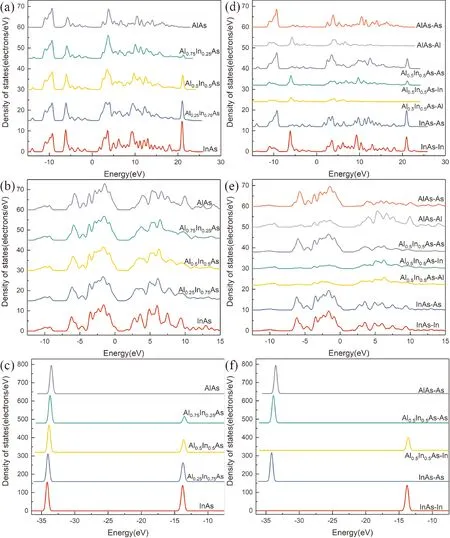
图4 AlxIn1-xAs体系分波态密度Fig. 4 Partial density of state ofAlxIn1-xAs
3.2.2分波态密度
对各组分AlxIn1-xAs晶体计算其分波态密度,计算结果如图4所示,其中图4 (a)、(b)、(c)分别对应各组分AlxIn1-xAs晶体在S、P、D轨道上的态密度,而图4 (d)、(e)、(f)则分别展示了各原子在S、P、D轨道上的态密度.
计算结果显示,各组分AlxIn1-xAs晶体的态密度区别明显. 由图4(a)可知,在S轨道上,InAs在能量为21 eV附近存在一个局域态,图4(d)显示其由In的5S轨道电子和As的4S轨道电子贡献,当In原子逐渐被Al原子取代时,此局域态的可容纳电子数逐渐减少. 同时,-10 eV附近的局域态主要由As原子贡献,而-6 eV附近的局域态由Al原子和In原子贡献. 图4(b)显示在P轨道上,各组分AlxIn1-xAs晶体的分波态密度情况类似,而由图4(e)展示的各原子对态密度的贡献来看,AlAs与InAs的各组成原子对其P轨道态密度均有贡献,而Al0.5In0.5As则由As原子提供绝大部分贡献. 图4(c)显示在D轨道上,InAs在能量为-34 eV附近存在一个局域态,图4(f)显示其由As原子单独贡献,且此局域态随着Al组分增加,发生蓝移现象[15]. 能量在-13 eV附近的局域态由In原子单独贡献,随着In组分降低,此局域态将逐渐减小直至消失. 此外,Al原子对D轨道的能态密度没有贡献.
3.3 光学性质
众所周知,材料的光学特性可以通过介电函数来描述,通过它可以获得各种光谱信息[16],其表达式为:
ε(ω)=ε1(ω)+iε2(ω)
(3)
其中ε2为介电函数的虚部,其大小能够直观反映电子受激跃迁的程度,虚部值越大,则代表电子越容易吸收光子并发生跃迁. 介电函数虚部ε2的表达式如下:
δ(Ej, k-Ei, k-w)d3k
(4)
其中e是电子电荷,m是自由电子的质量,ω是入射光子的频率,i和j分别代表初始状态和最终状态,M是偶极矩阵.fi表示第i态的费米函数分布.
实部ε1则与介质中储存的能量有关,根据Kramers-Kronig变换,介电函数实部ε1可以由虚部ε2得到:
(5)
本文分别计算了Al0.25In0.75As、Al0.5In0.5As及Al0.75In0.25As等三种组分的介电函数虚部ε2,结果如图5(a)所示.
计算结果显示,Al0.25In0.75As与Al0.5In0.5As在3eV附近存在介电函数虚部峰,结合Al0.5In0.5As分波态密度结果,如图5(b)所示,此峰值是由As-4p态与As-4s态之间的电子跃迁产生的,此过程在图中标记为①. 相较之下,Al组分更高的Al0.75In0.25As的介电函数虚部向高能区域偏移,这与其禁带宽度更大的趋势相对应. 同样,Al掺杂Mg2Si等半导体材料时,对其介电性质也有着相似的影响[17].
根据式(6),吸收系数可由介电函数推导定义,作为对照,本文依旧选取Al0.25In0.75As、Al0.5In0.5As及Al0.75In0.25As等三种组分进行计算,结果如图6所示.
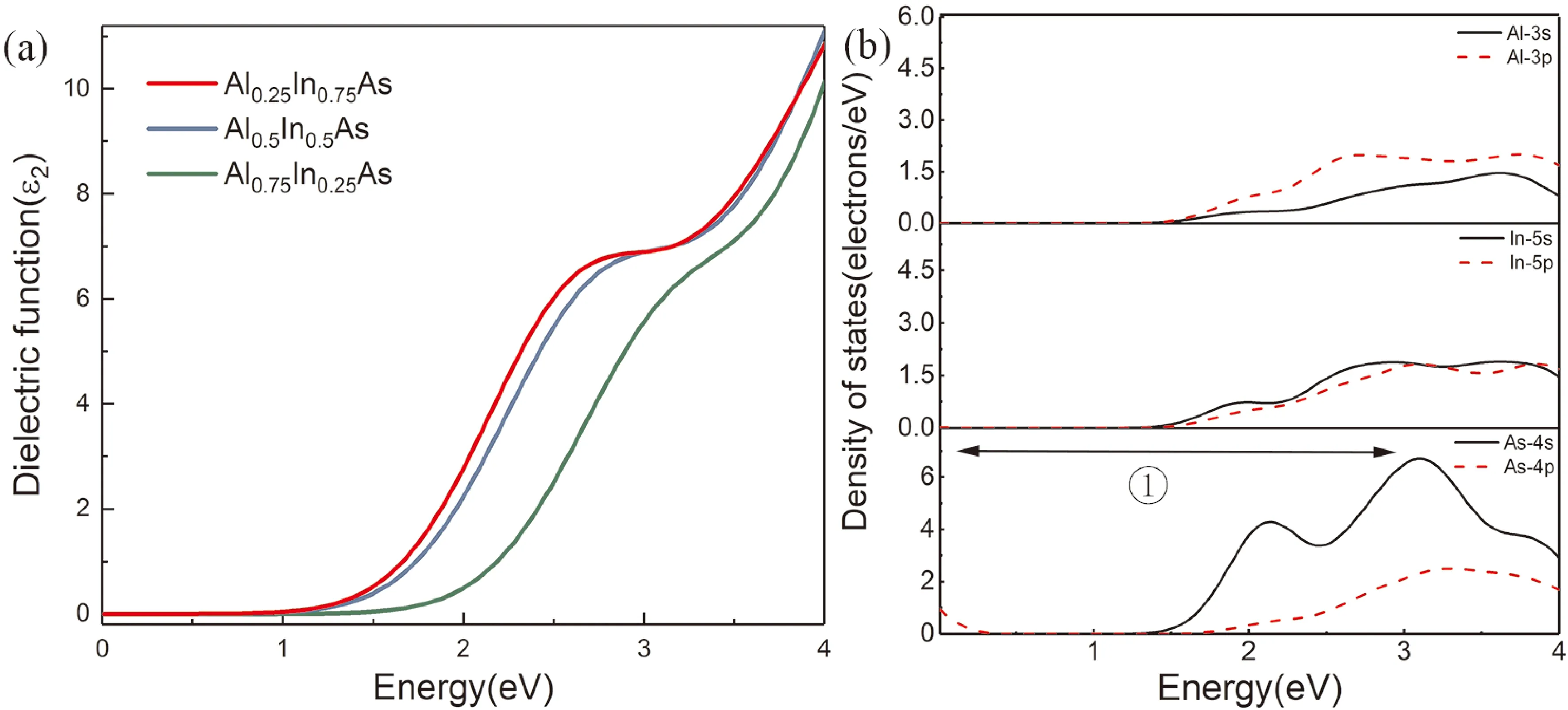
图5 AlxIn1-xAs体系的介电函数及Al0.5In0.5As分波态密度Fig. 5 The dielectric coefficient for AlxIn1-xAs and PDOS of Al0.5In0.5As

图6 AlxIn1-xAs体系的吸收系数Fig. 6 The absorption coefficient for AlxIn1-xAs
(6)
与Al0.5In0.5As相比,In组分更高的Al0.25In0.75As在可见光范围内吸收强度更大,这缘于其更小的禁带宽度,价带电子被激发至导带所需的能量更少,因而吸收光谱边缘红移,光谱响应范围更广. 同理,由于存在更大的带隙,Al0.75In0.25As的吸收边缘相较Al0.5In0.5As发生蓝移,吸收边约为1.8 eV,与其带隙宽度基本一致.
4 结 论
基于密度泛函理论,对各组分AlxIn1-xAs的晶体结构,电子结构及光学性质进行计算. 计算结果显示,随Al组分增加,AlxIn1-xAs晶体各键长将不同程度地缩短,新形成的Al-As-Al键角相较原本的In-As-In角更大,而In-As-In键角变小. 此外,晶格常数随Al组分x的变化情况符合Vegard定律,随Al组分x的增加,AlxIn1-xAs晶胞体积迅速减小,禁带宽度变宽,且能带有从直接带隙结构转变为间接带隙结构的趋势,不同组分下的AlxIn1-xAs晶体态密度区别明显. 此外,在可见光范围内,更高In组分的AlxIn1-xAs晶体因存在更窄的带隙,在介电函数虚部及吸收系数上有更好的表现,光吸收能力更强,且光谱响应范围更广.
