地震作用下锚固滑坡的动力响应特性研究

任 祥，汪班桥，李 楠

(1.苏交科集团(甘肃)交通规划设计有限公司， 甘肃 兰州 730010；2.长安大学 地质工程与测绘学院，陕西 西安 710054)

工程实践表明，格构锚杆是一种有效的边坡(滑坡)支护方式，不仅抗滑显著，在抗震方面也具有明显的优势[1]，汶川地震、唐山地震以及日本Hanshin-Awaji地震调查后的结果均发现锚固工程在震后仍然有效，基本未出现明显地质灾害.因此充分了解锚固边坡的地震响应、格构锚杆的抗震机理对于高烈度地区边坡防护的抗震设计尤为重要.

目前，很多学者依据数值模拟、振动台试验等手段针对锚固边坡进行了研究，并取得一些研究成果.汪班桥、郝建斌[2-3]使用硅胶材料模拟土体开展格构锚杆支护滑坡的小型振动台试验，研究了地震作用下锚杆的受力机制和锚固滑坡的加速度、位移响应，但地震波在硅胶材料的传播特性能否真实反映土体的传播特性值得商榷.蒋良潍[4]采用振动台模型试验对坡面效应的产生机理及锚固控制机理进行了初步研究，但对锚杆的动力响应没有分析.赖杰[5]依托振动台模型试验，研究了抗滑桩和锚杆联合支护下的边坡抗震性能，对同一锚杆的受力特性进行了分析，但并未涉及到不同位置的锚杆受力特性.QI Wenjin[6]、DONG Jianhua[7]利用数值模拟软件研究了地震作用下预应力锚杆边坡动力响应，分析了预应力对边坡地震性能的影响.叶帅华[8]同样利用数值模拟软件研究了动力作用下地震烈度、锚杆长度和锚杆间距等对边坡稳定性的影响.然而，模拟成果得不到试验验证，难以直接指导工程设计.

为更合理的进行锚固滑坡抗震设计，本文依托大型振动台模型试验，以格构锚杆支护、有明显滑面的土质滑坡为研究对象，对不同强度地震激励作用下锚固滑坡的加速度响应、各层锚杆的受力特性等规律进行研究，以期更好地为工程实践服务.

1 振动台试验设计

试验在西安建筑科技大学结构抗震试验室进行.主要技术参数：最大载重20 t；台面尺寸4.1 m×4.1 m；工作频段0.1～50 Hz；最大位移：水平X向±15 cm，水平Y向±25 cm，竖向±10 cm；最大加速度：水平X向±1.5 g，水平Y向和竖向±1.0 g.

模型箱由角钢和厚1cm的可透视有机玻璃板构成，箱体长×宽×高为：2.05 m×1.5 m×1.3 m.填筑模型前，于箱底部铺粘一层碎石，以减少箱土接触面的相对位移；箱体前后两侧分别黏贴5 cm厚的聚乙烯泡沫板以减小边界效应.

1.1 相似比设计及相似材料选定

试验原型为一高7 m的土质滑坡，坡度为60°，锚杆间距为2 m×1.5 m.依据试验条件，设定试验的几何相似比7，试验模型的坡高为1m，锚杆间距为0.29 m×0.22 m，如图1所示.相似关系按照量纲分析法进行推导，选取长度、密度、加速度作为基本控制量，其中，Sp=1,Sa=1,Sl=7，其余物理量利用π项式和相似准则方程导出，如表1.

土体力学性质复杂，随组分、应力状态、荷载水平和加载频率等的不同而变化，并在低应变水平时就开始出现非线性，很难找到一种能全面考虑这些特性和影响因素的模拟材料[9].本试验模型的滑床及滑体均采用西安地区的黄土分层夯筑而成，压实系数0.93，实际夯实后的土体重度18.9 kN/m3，含水率14.6%；滑带由铺设于滑床上一层厚2～3 mm的干细土模拟.

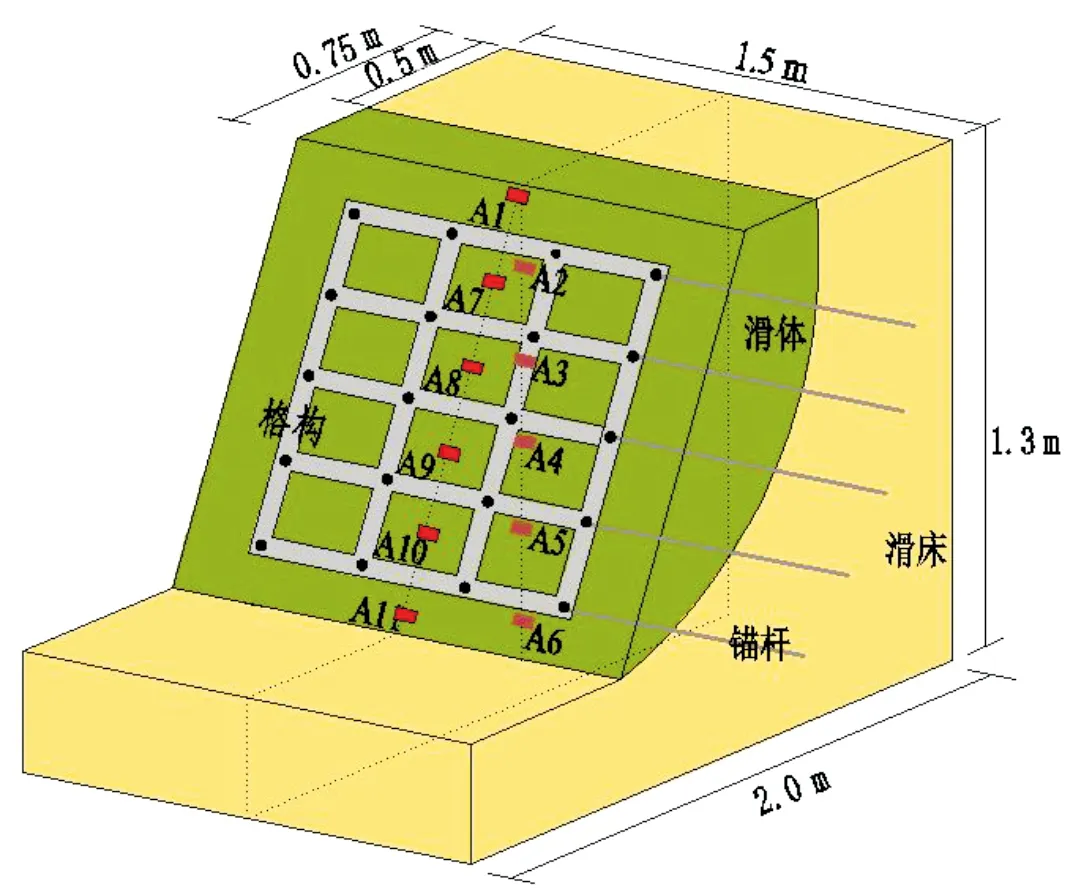
图1 模型立面图Fig.1 Elevation drawing of the model

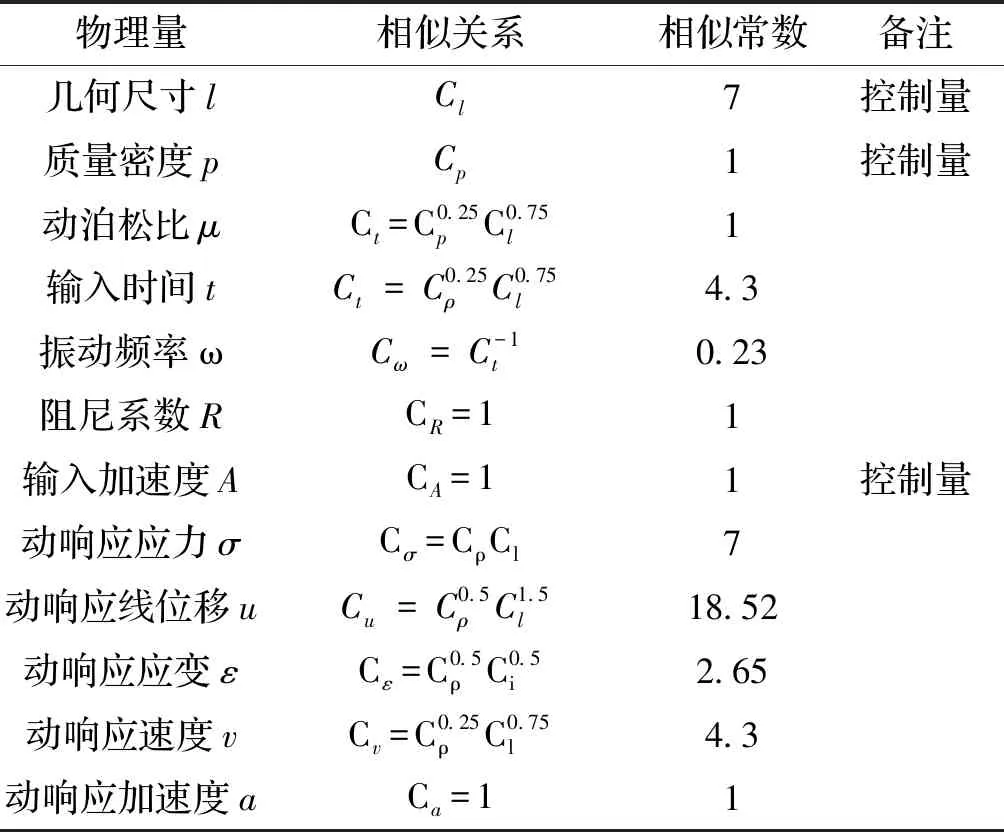
物理量相似关系相似常数备注几何尺寸lCl7控制量质量密度pCp1控制量动泊松比μCt=C0.25pC0.75l1输入时间tCt=C0.25ρC0.75l4.3振动频率ωCω=C-1t0.23阻尼系数RCR=11输入加速度ACA=11控制量动响应应力σCσ=CρCl7动响应线位移uCu=C0.5ρC1.5l18.52动响应应变εCε=C0.5ρC0.5i2.65动响应速度vCv=C0.25ρC0.75l4.3动响应加速度aCa=11

锚杆和格构是在几何相似比Sl=7的基础上，按规范设计计算确定的.锚杆类型为全长无粘结压力型锚杆，锚孔直径为2 cm，采用光面消除应力的Φ6 mm钢筋模拟杆体，2 cm厚的Q235圆环钢板，通过螺帽固定在端头模拟承载板，钢筋上涂抹凡士林后缠裹塑料胶带以实现锚筋与砂浆脱粘模拟全长无粘结特性.灌注砂浆配合比为水：水泥：细砂=40:29:145.格构梁的制作是通过浇筑绑扎好的铝筋笼(4Φ6)来完成，其中混凝土强度等级为C10，配合比为水：水泥：细砂：细石=0.8:1:2.96:3.76，截面尺寸为40 mm×50 mm.

1.2 测点布设

为监测不同高度处锚固滑坡的加速度响应，在坡内(测点A1、A3、A4、A5、A6)及坡面(测点A7、A8、A9、A10、A11)埋设11只加速度传感器，如图1.振动台台面上安装1只加速度传感器作为激励控制.

为监测锚杆的轴力响应，锚杆的杆身黏贴4只应变片(BE-120)，具体位置如图2.

图2 杆身应测点布设Fig.2 Layout of the measuring points of anchor

1.3 激励地震波

试验激励波有：汶川波(中国四川、2008年)、EL Centro 波(美国加州、1940年)，其加速度时程及傅里叶谱如图3所示.由于水平地震作用显著降低边坡稳定性，是结构破坏的主要因素，因此本试验地震波均为单向水平输入.

试验加载机制采用逐级增大加载强度的方式进行，输入加速度峰值顺序依次为0.05 g、0.1 g、0.15 g、0.2 g、0.3 g、0.4 g、0.6 g.为获取锚固滑坡的自振频率f、阻尼比、振型等动力特性，试验开始前、加速度峰值改变时及试验结束后分别对模型进行峰值为0.035 g的白噪声频谱扫描.

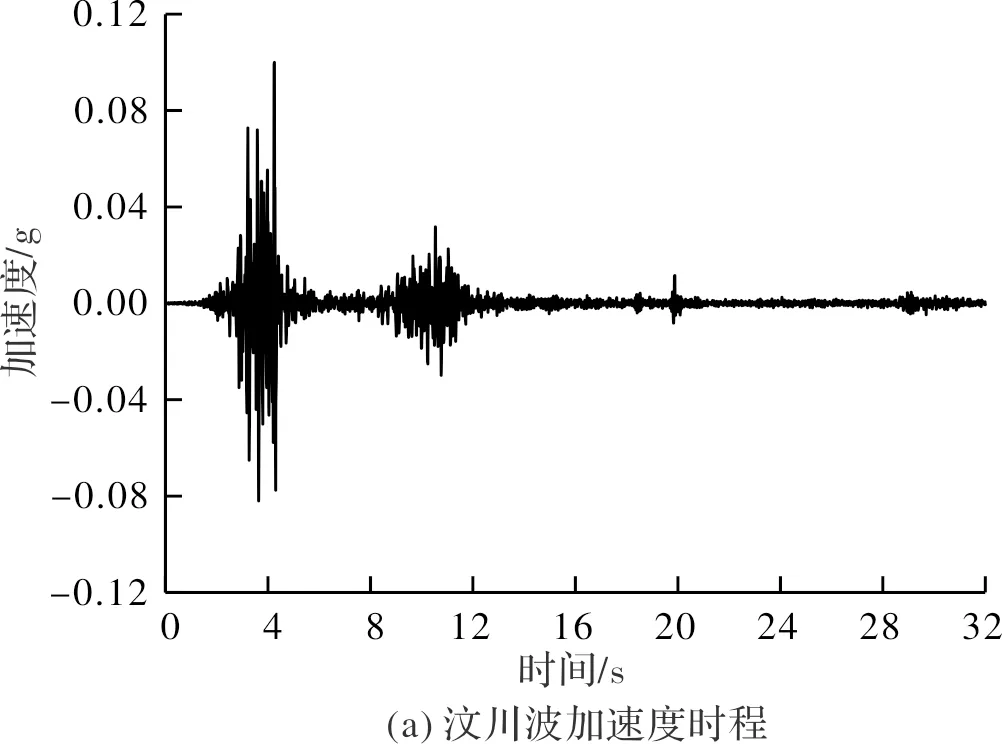
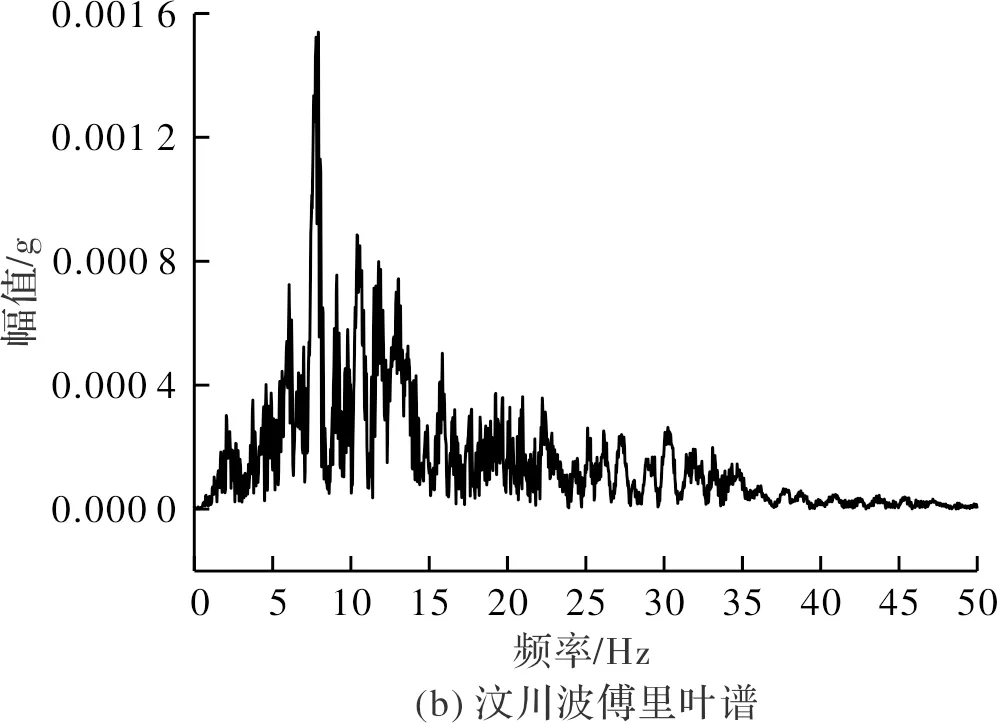
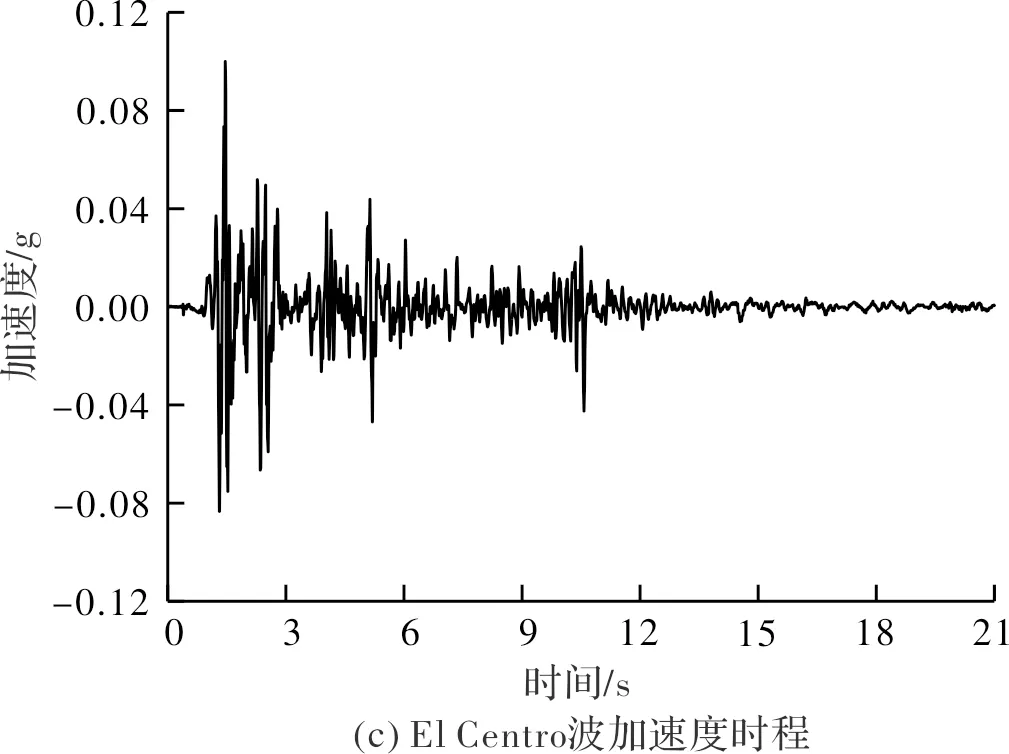
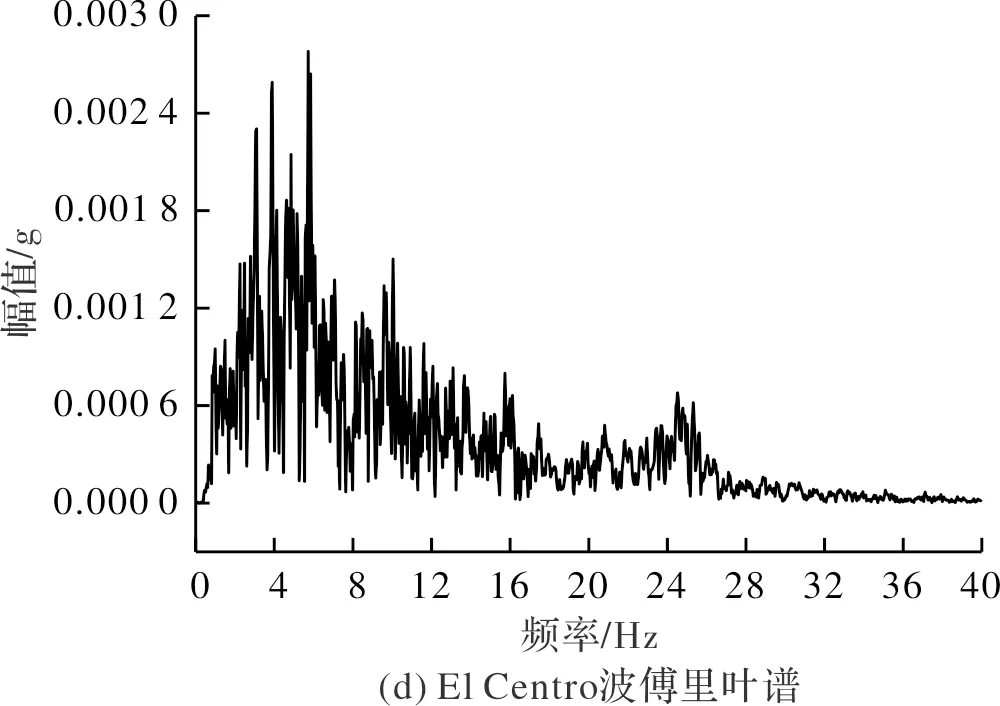
图3 输入地震波的加速度时程曲线及傅里叶谱Fig.3 Acceleration time history and Fourier spectrum of seismic waves

2 试验结果分析

2.1 同高程坡内测点与坡面相应测点的PGA对比分析

黄润秋等[4、14]通过振动台试验及野外调查发现自然边坡地震失稳一般表现为浅表崩滑，呈现出“剥皮型”灾害特点.为分析地震激励作用下锚固边坡的坡面效应，将传感器上的加速度响应峰值与台面输入的加速度峰值比值定义为PGA放大系数(全文下同)，对同一高程坡内测点与坡面相应测点的PGA放大系数进行对比分析.以汶川波为例，表2为各级加载强度下同一高程处坡内测点与坡面相应测点的PGA值.

加载强度从0.05 g逐步升至0.6 g，各测点的PGA值也不断增大；但无论是在低强度还是在高强度加载下，坡面各测点(A7、A8、A9、A10、A11)与坡内相应测点(A2、A3、A4、A5、A6)的加速度响应非常接近，并未出现自然滑坡中的坡面效应；试验过程中也未发现格构锚杆支护的坡面土体出现松动、裂缝、“剥皮”等现象.这主要是因为地震波激励作用下，锚杆主动支护边坡，格构梁、锚杆及坡内土体成为一体，共同抗滑；较高的整体性抵消了地震波在坡面反射引起的坡面效应.

2.2 同列测点加速度响应分析

以坡内同列测点A1、A2、A3、A4、A5、A6为例，对锚固滑坡在不同加载强度下的加速度响应进行分析.图4(a)(b)、图5(a)(b)分别为汶川波和El Centro波激励下各测点PGA及PGA放大系数随加载强度的变化曲线.

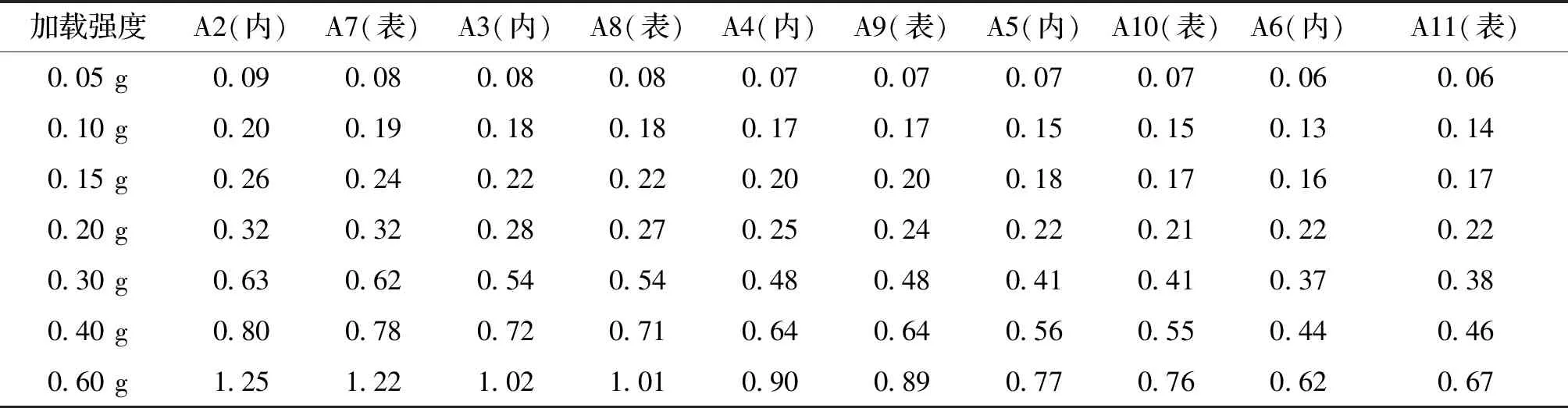
表2 汶川波激励下各测点PGA值

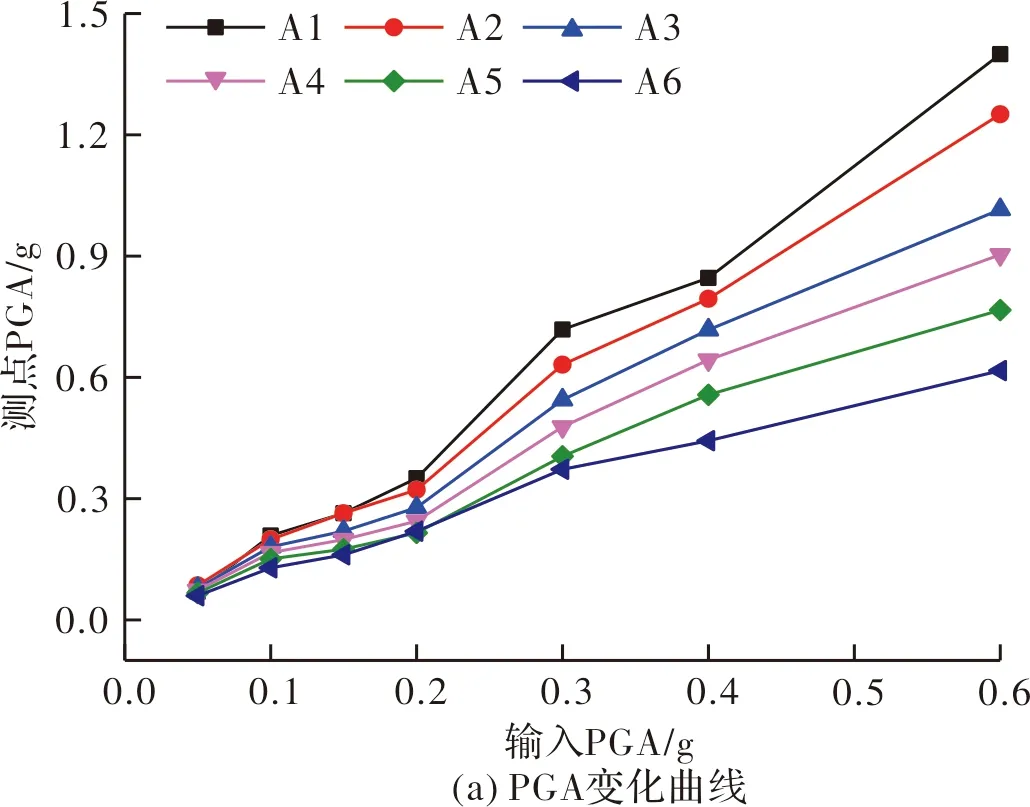
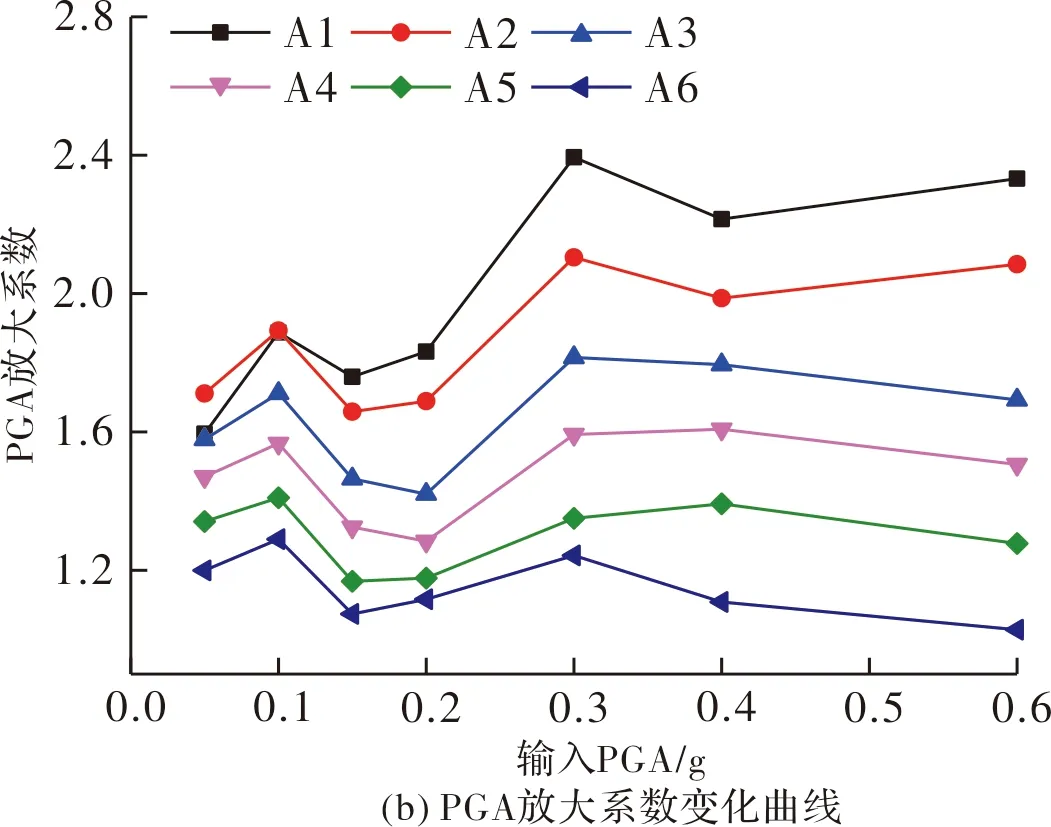
图4 汶川波激励下各测点加速度响应随加载强度的变化Fig.4 Acceleration response of measuring points with the loading magnitude at Wenchuan wave

(1)地震波激励强度从0.05 g逐步升至0.6 g，不同高程各测点的PGA曲线和PGA放大系数曲线变化趋势一致；均呈现“高程放大效应”，即高程越高，加速度响应越强；与锚固滑坡 “上大下小” 的加速度振型一致.

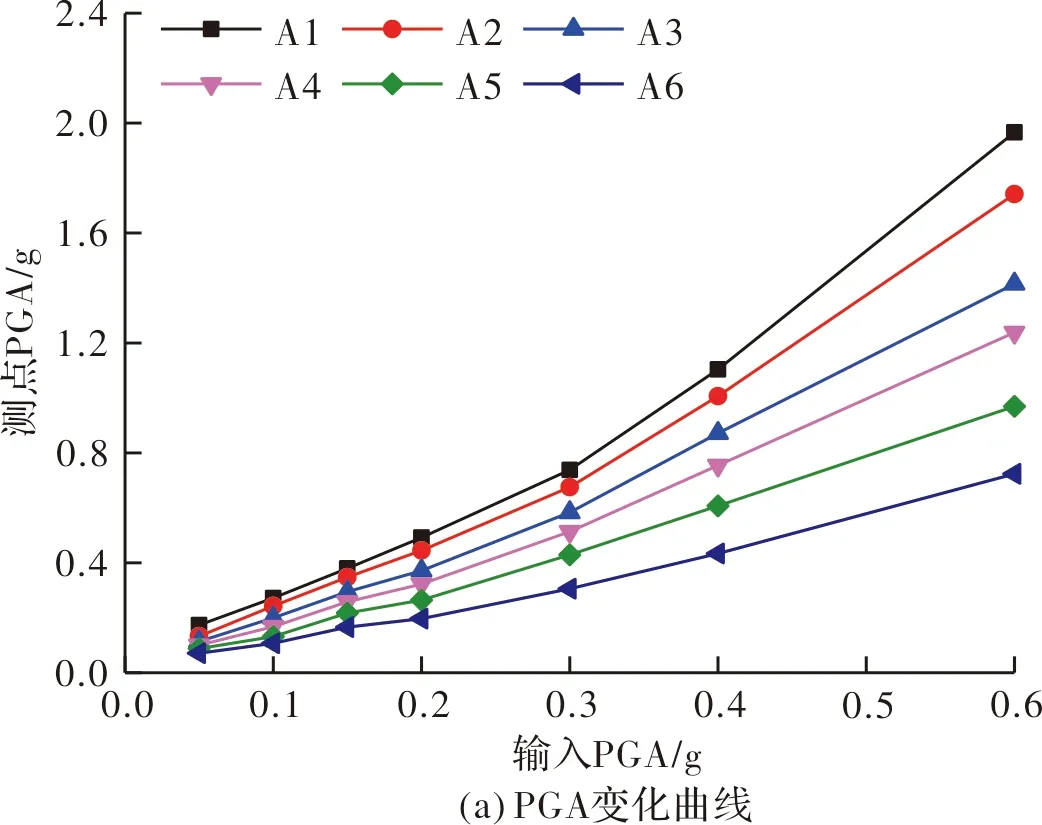
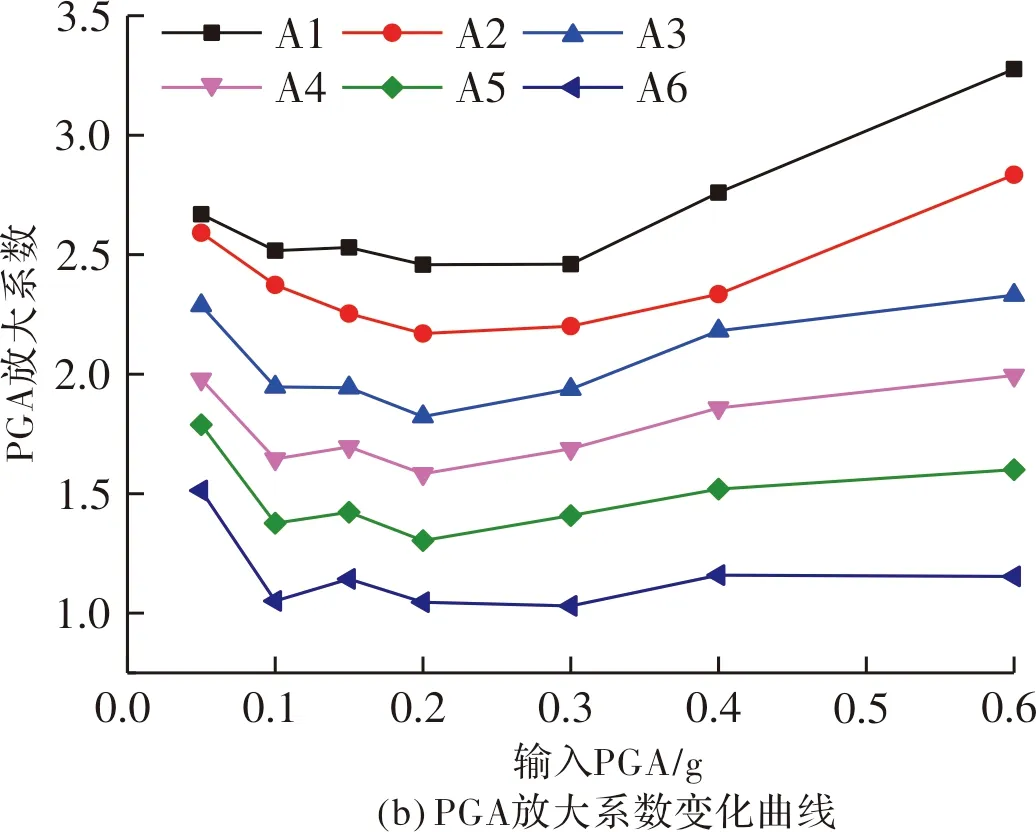
图5 El Centro波激励下各测点加速度响应随加载强度的变化Fig.5 Acceleration response of measuring points with the loading magnitude at El Centro wave

(2)无论是El Centro波激励还是汶川波激励，随着激励强度增大，锚固滑坡各测点PGA值均逐渐增大.低强度地震波激励作用下(0.05～0.2 g)，随加载强度增大，测点PGA值增长较缓慢，不同高程处的测点PGA曲线比较密集，锚固滑坡各层监测点的地震响应差异较小.0.2 g之后，各测点加速度响应均得以增强，且各层测点PGA曲线分布相对稀疏，说明在较高量级地震作用下锚固滑坡的高程效应越来越显著，各层监测点的不协调变形增大.

(3)地震波不同，频谱特性不同，其在土体内部的传播特性也有差异.因此，在El Centro波和汶川波两种不同的激励作用下，随加载强度的增大，锚固滑坡呈现不同的非线性放大特征，但总体趋势较接近.低强度加载(0.05～0.2 g)下，锚杆格构支护结构的主动抗滑抗震作用还未完全发挥，模型土体出现非线性，其抗剪强度及剪切模量逐渐减小，土层水平剪切作用自下而上的传播速度降低， PGA放大系数有所减小.中、高强度加载时，锚杆格构发挥的作用增强，锚杆、格构和滑坡土体协同工作、相互牵制，整体性增强，各测点PGA放大系数有所增加.

整体而言，随加载强度的增大，PGA曲线和PGA放大系数曲线越来越分散，锚固滑坡的上下不协调变形越来越明显，各测点的高程放大效应也随之越来越显著.

2.3 锚杆的动力响应分析

试验锚杆设计为5层4列，自上而下分别为第一层(顶层)、第二层、第三层、第四层、第五层(底层)，由于试验模型为对称结构，本文以第二列锚杆为例进行分析.为方便比较不同层锚杆的轴力响应，取每根锚杆上S1、S2、S3和S4测点的轴力峰值平均值作为锚杆的轴力峰值.测点轴力与应变之间的换算关系如式(1).

F=EAε

(1)

式中：F为轴力；E为锚筋弹性模量，本试验取2×105N/mm2；A为锚筋面积，取28.26 mm2；ε为测点应变.

图6、图7分别为汶川波激励和El Centro波激励下各层锚杆的受力情况随加载强度的变化曲线.

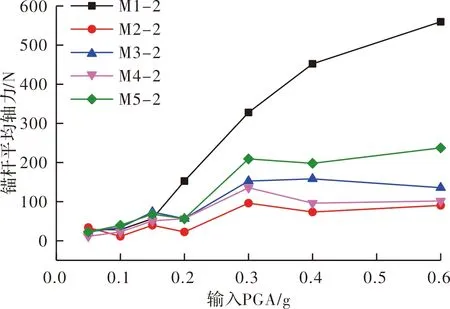
图6 汶川波激励下各层锚杆平均轴力峰值随加载强度的变化Fig.6 Stress characteristics of anchors and lattice beams with the loading magnitude at Wenchuan wave

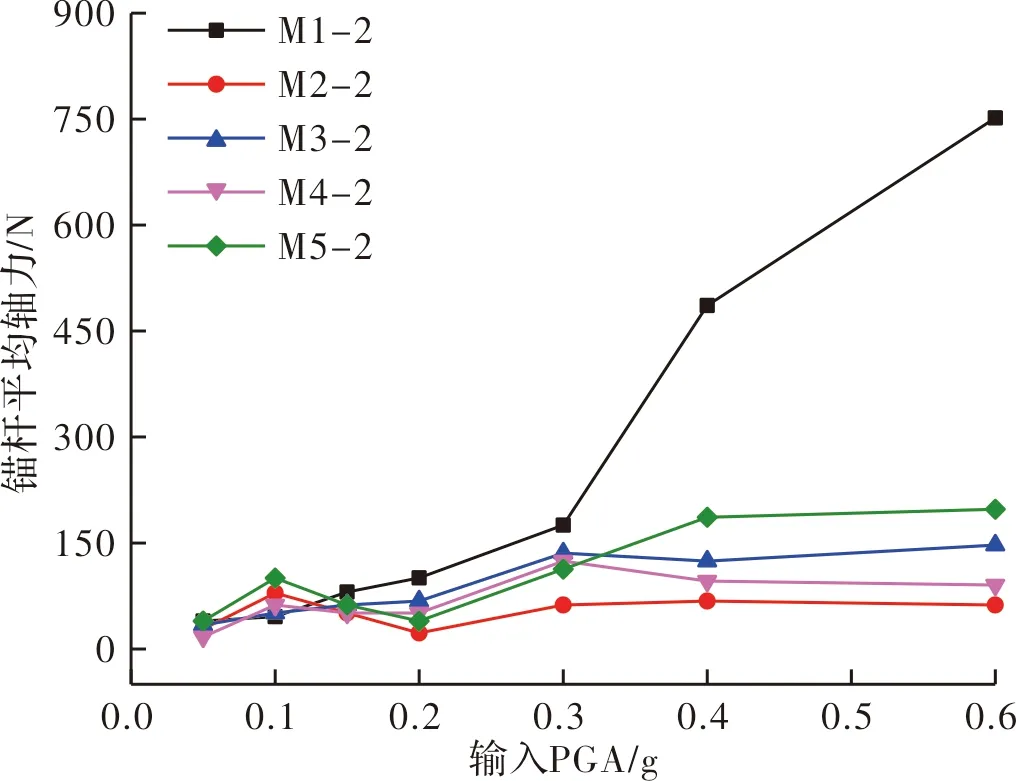
图7 El Centro波激励下各层锚杆平均轴力峰值随加载强度的变化Fig.7 Stress characteristics of anchors and lattice beams with the loading magnitude at El Centro wave

和2.2节加速度响应结果吻合，0.05～0.15 g低强度加载下，各层锚杆的动力响应差异不大，锚杆平均轴力峰值曲线分布密集，且数值较小.0.2～0.3 g加载时锚固滑坡的上下不协调变形开始增大，锚杆主动抗震抗滑作用略有增强，顶层锚杆的轴力值开始增大；0.4～0.6 g高强度加载时，锚固滑坡上下不协调变形明显，顶层锚杆的锚固力急剧增大.

总体而言，低强度加载下，锚杆主动抗震抗滑特性未完全发挥，各层锚杆的轴力峰值差异不大，底层锚杆的轴力峰值略高于其他四层.这与静力加载下锚杆格构的受力情况接近，坡脚处剪应力较集中、底层锚杆受力相对较大[16].随着加载强度的增大，锚杆主动抗震抗滑特性增强，各层锚杆受力情况发生了调整，最终调整为“第一层(顶层)>第五层(底层)>第三层>第四层>第二层”，且顶层受力随载强度增大而增大的趋势越来越明显，其他四层则趋于稳定.

因此，在抗震抗滑设计时，除遵循“强腰固脚”的原则外，还应特别注意增大顶部锚杆和顶层横梁的安全储备；另外，滑体顶部容易在高强度地震下发生崩塌，建议在高烈度地区进行格构锚杆支护滑坡时，加长顶部锚杆、种植根系发达的植物或坡顶垂直打入微型桩进行支护.

3 结论

通过大型振动台试验，研究了汶川波和El Centro波各加载强度作用下格构梁锚固滑坡的加速度响应、锚杆的受力特性等动力响应规律.

(1)坡体各高程测点的加速度响应 “上大下小”， 与锚固滑坡 “上大下小” 的加速度振型一致.同一高程处坡面与坡内加速度响应接近，锚固结构的支护在一定程度上避免了自然边坡中普遍存在的坡面效应，对滑坡起到了有效的抗震效果.

(2)低强度加载下，各测点PGA放大系数随着加载强度的变化略有减小；中、高强度加载下，锚杆格构主动抗震抗滑特性增强，锚杆格构梁锚固滑坡的整体性增强，各测点PGA放大系数随加载强度的变化表现为逐渐增大然后趋于稳定.

(3)随着加载强度的增大，锚杆主动抗震抗滑特性增强，各层锚杆受力情况发生了调整，最终调整为“第一层(顶层)>第五层(底层)>第三层>第四层>第二层”，且顶层受力随载强度增大而增大的趋势越来越明显，其他四层则趋于稳定.

(4)由于本次试验仅做了一组锚杆格构支护滑坡模型，没有做同等条件下的自然滑坡，因此未能更详细、更具体的对比有无锚杆格构支护滑坡的动力特性差异，这是本文试验的一个缺陷.