基于L1/2正则化理论的地震稀疏反褶积
2019-12-06康治梁张雪冰
康治梁,张雪冰
(1.成都理工大学地球物理学院,四川成都610059;2.加拿大多伦多大学物理学院,安大略多伦多,ON M5S 1A7;3.吉林建筑大学测绘与勘查工程学院,吉林长春130118)
随着油气勘探开发的不断深入,小尺度(薄互层)岩性油气藏的识别已成为愈发重要的问题[1],在褶积模型的假设下,要求能够从地震信号中反褶积出准确的反射系数信息,包括它的位置和振幅[2]。有限频地震信号的反褶积常常是一个多解问题,而在实际应用中,地质模型的成层性决定了我们需要的是具有稀疏性质的解[2]。压缩感知理论的信号恢复问题就是求解信号在某个基底下的稀疏表示系数,这与地震反褶积有类似之处。VELIS[2]将模拟退火算法和线性最小二乘法相结合,求取反射系数序列中脉冲的时间位置和振幅,然而模拟退火算法非常耗时,应用于大规模数据的计算成本较高。匹配追踪(MP)算法可用于稀疏问题的求解,YANG等[3]利用MP算法实现了压缩感知框架下的重力信号恢复,但MP算法通常在信号超稀疏且噪声不显著时才有优势[4]。目前广泛使用的稀疏问题求解办法是L1正则化约束。ZHANG等[5]认为地震反射系数可以用一系列代表楔状模型的奇偶字典线性表示,求取表示系数时使用L1范数进行稀疏性约束,实现了模型约束意义下的反演。OLIVEIRA等[6]使用L1正则化约束实现了衰减介质中的稀疏反褶积。余慧敏等[7]利用L1正则化约束实现了压缩感知框架下的探地雷达成像。蒋川东等[8]实现了基于L1范数的低场核磁共振T2谱稀疏反演。然而,压缩感知理论的一些实践表明,在稀疏恢复能力和适应噪声方面,L1正则化不是最佳的稀疏正则化[9],这也启示我们必须在地震稀疏反褶积中寻找更好的稀疏约束方法。
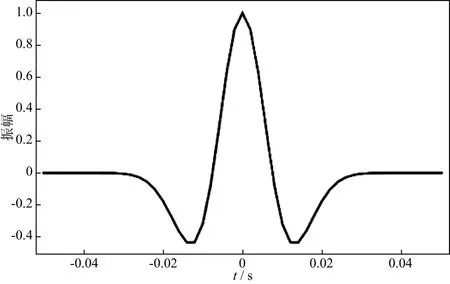
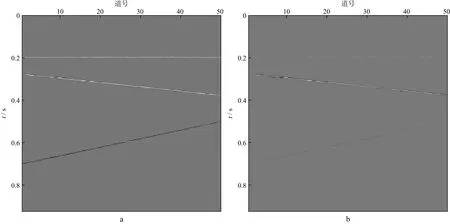
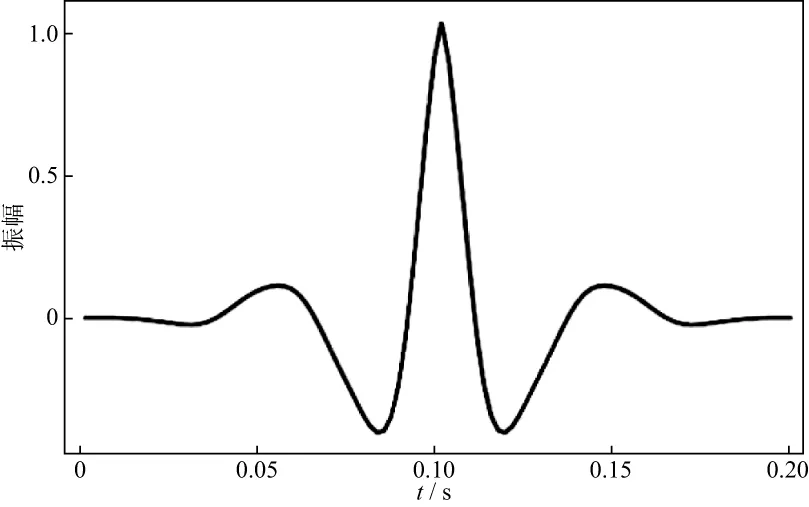
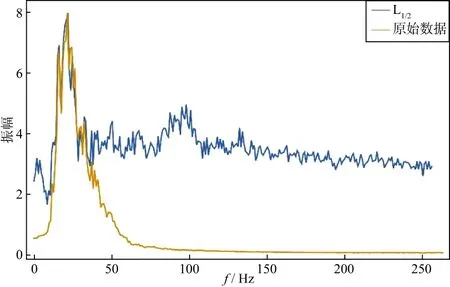
XU等[10-12]对非凸的Lq(0 在自激自收条件下,ROBINSON[17]提出利用褶积模型描述地震响应,地震记录可近似看作是地震子波与地层反射系数的褶积结果,即: s(t)=w(t)*r(t)+n(t) (1) 式中:s(t)表示合成地震记录;w(t)表示地震子波;r(t)表示反射系数序列;n(t)表示随机噪声。在矩阵格式下(1)式可以表达为: s=Wr+n (2) 式中:W为卷积核矩阵。求取反射系数问题通常存在多解性,然而层状地层的假设决定了反射系数r是一个稀疏脉冲序列,于是反褶积问题可以描述为在约束条件下的稀疏求解问题。 min‖r‖0s.t.s=Wr+n (3) 式中:‖r‖0是L0范数,代表向量的非零项系数的个数。类似(3)式的稀疏问题也可以从压缩感知理论导出。由压缩感知理论可知,当信号在某个基底下能稀疏表示时(如余弦变换基、小波变换基),可以用低于奈奎斯特采样率的方式感知信号,且仍能高概率地恢复出信号[18]。压缩感知的信号恢复问题可以表示为: min‖x‖0s.t.y=φψx+ε (4) 式中:ψ表示基底;φ表示测量矩阵;y表示测量值(维度小于原始信号维度);x表示原始信号的稀疏表示系数;ε表示噪声。可令A=φψ。(3)式和(4)式都可以直接建模为L0正则化问题[12],以反褶积为例: (5) 式中:λ是正则化参数。我们面临的问题是,L0正则化问题是一个NP-hard问题,无法直接求解。已有的许多关于压缩感知和稀疏反演的文献中,问题((5)式)通常凸松弛为L1范数问题[12]: (6) L1范数问题是凸优化问题,常见算法包括梯度投影法、同伦法、迭代收缩阈值法、近似梯度法和增广拉格朗日乘子法[19]。本文使用迭代收缩阈值算法(iterative shrinkage-thresholding algorithm,ISTA),BECK等[20]给出了该算法的详细推证。ISTA算法源自一般化的最小化问题: (7) (8) 式中:tk为步长。对于L1范数问题((6)式),f(x)=‖s-Wr‖2,g(x)=‖r‖1,(8)式进一步转化为: (9) 问题(9)由于变量可分,rk的每一个分量可以通过求解一个简单的软阈值函数Tsoft得到: rk=Tsoft[(rk-1-2tkWT(Wrk-1-s)] (10) 同时算法收敛要求步长tk满足tk∈(0,1/‖WT·W‖)。 尽管L1范数约束已被广泛使用,但压缩感知领域的研究结果表明,使用L1范数约束不能保证有最稀疏的结果,也不能确保在较小采样率的情况下精确恢复信号[12],此外,从地震稀疏反褶积得到的结果也能发现,L1范数约束得到的结果在幅值上与真实反射系数的拟合度也有不足[21]。 针对L1范数存在的问题,XU等[10-12]系统地研究了形如(11)式的Lq正则化问题,提出了“L1/2正则化理论”。 (11) XU等[10-12]通过压缩感知研究方面的大量计算证实,q∈(0,1/2]时,Lq正则化性能没有显著差异,q∈(1/2,1]时,Lq正则化性能递减,他们的工作揭示了L1/2正则化在各种稀疏约束中的突出的代表性现象。L1/2正则化是非凸的,常规的凸优化工具难以求解,XU等[12]基于严格的数学分析给出了求解L1/2正则化问题的特定阈值迭代算法,使得该问题能快速高效地求解。该算法的迭代格式为: xn+1=Hλ(B(xn)) (12) Hλ(x)=(hλ(x1),hλ(x2),…,hλ(xn))T (13) 其中,hλ(·)定义为: (14) XU等[12]有针对性地对比了L1/2正则化和L1正则化在压缩感知信号恢复问题研究方面的性能差异,在有噪声和无噪声条件下,L1/2正则化的恢复精度都更高,且对欠采样的稳健性更强。这些工作为我们提供了另一种地震稀疏反褶积的思路,即将L1/2范数作为反射系数的稀疏约束项,并用该特定阈值迭代算法进行求解。 本文假设子波已知,实验中选取主频为30Hz的雷克子波(图1)。在实际处理中,子波可以从地震记录中通过盲提取获得,如利用高阶统计量的方法[22]。 在各类正则化问题中,正则化参数λ对反演效果有显著的影响。通常依赖经验来设定λ,为了对比在常规取值范围内、不同λ条件下L1/2范数约束和L1范数约束的反演效果,构建了一个简单的反射系数序列(图2a),时间采样间隔为2ms,合成对应的地震数据,并加入15%的噪声,结果见图2b所示。本文使用SRE(signal-to-reconstruction error)来评价反演效果,SRE定义为: (15) 图1 实验中使用的子波 图5a是构建的另一个反射系数模型,图5b是对应的加入了15%噪声的合成地震记录。分别用L1和L1/2范数约束进行反褶积,结果如图6a和图6b所示,图7a和图7b是对应的反演结果与真实反射系数的残差。综合图6和图7可以看出,这两种稀疏约束均能得到较准确的反射系数模型形态特征,但L1/2范数约束的残差更小,能更好地保护反射系数幅值。 图2 简单的稀疏反射系数模型(a)及其含噪的合成地震数据(b) 图3 SRE值与λ的关系(横坐标为对数坐标) 图4 SRE值与噪声水平的关系 图5 简单反射系数模型(a)及其含噪的合成地震记录(b) 图6 采用L1(a)和L1/2(b)正则化约束得到的反褶积结果 图7 采用L1(a)和L1/2(b)正则化约束的残差 利用Marmousi2 P波速度模型的局部(图8红色方框中)构建了一个反射系数模型,如图9a所示。图9b和图9c分别为对应的不含噪声的和含20%噪声的地震记录,共150道,时间采样间隔为2ms。 图10是采用不含噪声的数据反演得到的结果,其中图10a是采用L1范数约束得到的结果,图10b是采用L1/2范数约束得到的结果。大体来看,采用这两种方法都能得到反射系数模型主要格架,但从标注红色方框的部分可以看出,采用L1范数约束得到的结果中存在反射系数缺失的情况,不利于横向连续性的保持和弱反射系数的保护,而采用L1/2范数约束能较好地保存反射系数信息,横向连续性好,刻画地层尖灭的能力更强。 图11是采用含噪声的数据反演得到的结果,其中图11a是采用L1范数约束得到的结果,图11b是采用L1/2范数约束得到的结果。由于噪声的存在,此时采用这两种方法反演的质量相比无噪声情形下的结果都有所下降。从红色方框指示的位置可以看到,采用L1范数约束得到的反射系数模型存在明显的层位缺失的现象,有的弱反射层被整体破坏;采用L1/2范数约束得到的反射系数模型虽然也存在缺失或振幅削弱的地方,但尚能保存大致轮廓,对地层格架特征的描述依然优于L1范数约束。 图8 Marmousi2 P波速度模型(空间采样间隔为1.25m) 图9 反射系数模型(a)和不含噪声的合成记录(b)及含噪声的合成记录(c) 图10 采用不含噪声数据的反演结果a L1正则化约束的结果; b L1/2正则化约束的结果 图11 采用含噪声数据的反演结果a L1正则化约束的结果; b L1/2正则化约束的结果 为了验证上述数值实验结果,对某实际二维地震数据进行了应用测试,其叠加剖面如图12所示。图13 是用统计性方法从实际地震记录中提取的子波。该区域薄层发育,纵向分辨率的提升十分必要。 图14是L1/2正则化约束反演结果,从标注红色方框的部分和箭头指示位置来看,L1/2正则化约束能够较好地揭示某些薄层结构的稀疏反射系数,有较强的刻画薄层和微小透镜体(箭头指示的部分)的能力,也能较好地保持原始地层模型的纵向展布特征。图15 展示了反褶积前、后地震数据频谱的变化,可以看出,采用本文方法反褶积之后,子波影响得到了有效消除,地震资料有效频带宽度显著提高,剖面的地层结构分辨率得到了明显提升。 图12 实际地震数据叠加剖面 图13 从实际地震记录中提取的子波 图14 采用L1/2正则化约束反演结果 图15 反褶积前、后的地震数据频谱 本文将用于压缩感知领域的L1/2正则化理论引入到地震稀疏反褶积中,采用了它的特定阈值迭代算法进行求解,形成了一种新的非凸正则化约束的稀疏反褶积方法。理论合成数据测试结果表明,L1/2正则化的表现优于L1正则化,适应噪声的能力更强,能更好地保护弱反射系数振幅。实际资料应用结果表明,L1/2正则化突出的稀疏表达能力,使它能够很好地刻画薄层结构和透镜体,为地震资料高分辨率处理提供了有力的工具。当然,作为一种数据处理手段,无论采用何种算法,反褶积的结果都需要其它手段验证,如测井信息的标定,这是实际工作中不能忽视的。 稀疏问题在地震信号处理中普遍存在,如基于原子库的信号稀疏分解,将信号用一系列具有特定时频特征的原子稀疏表示,可以达到去噪的目的,用L1/2正则化理论求取稀疏表示系数,有助于分离有效信息和噪声,这也是下一步研究方向之一。1 方法原理
1.1 稀疏反褶积


1.2 L1/2正则化理论
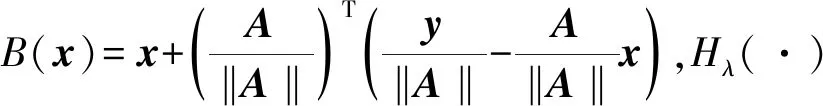
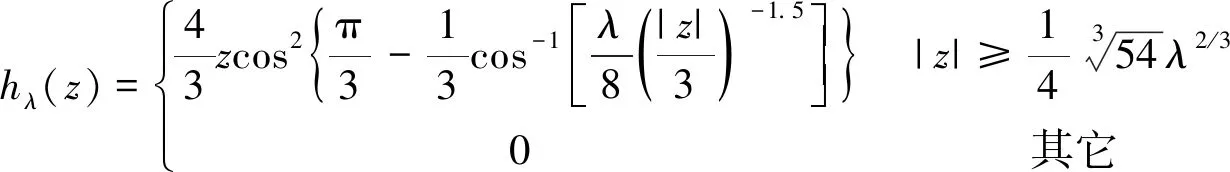
2 数值实验
2.1 简单模型






2.2 复杂模型
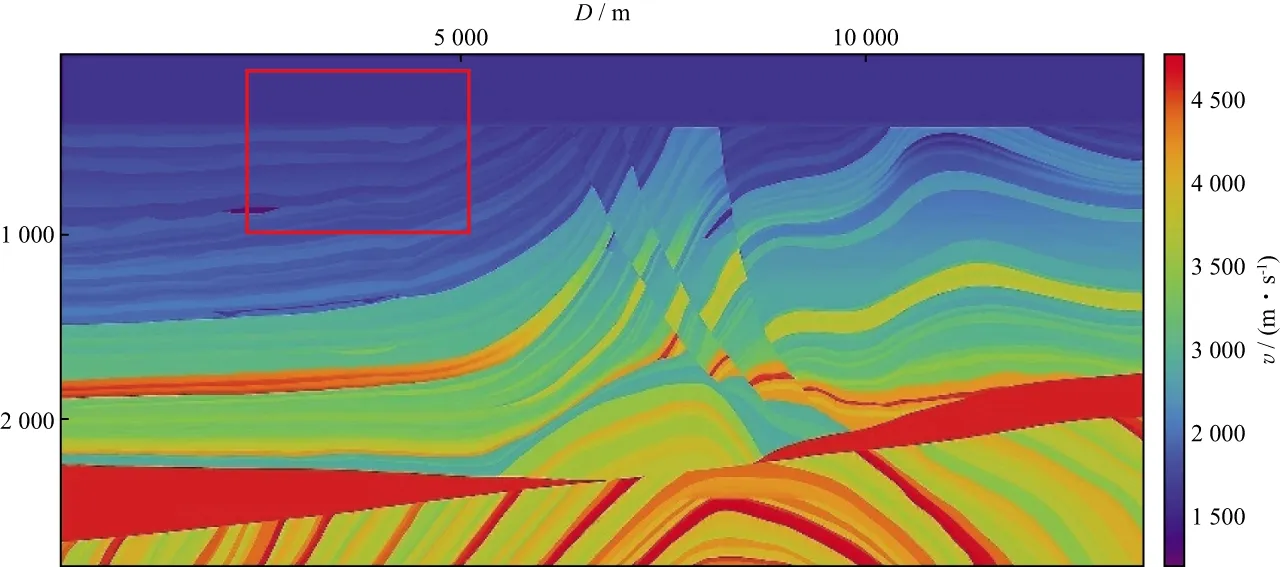
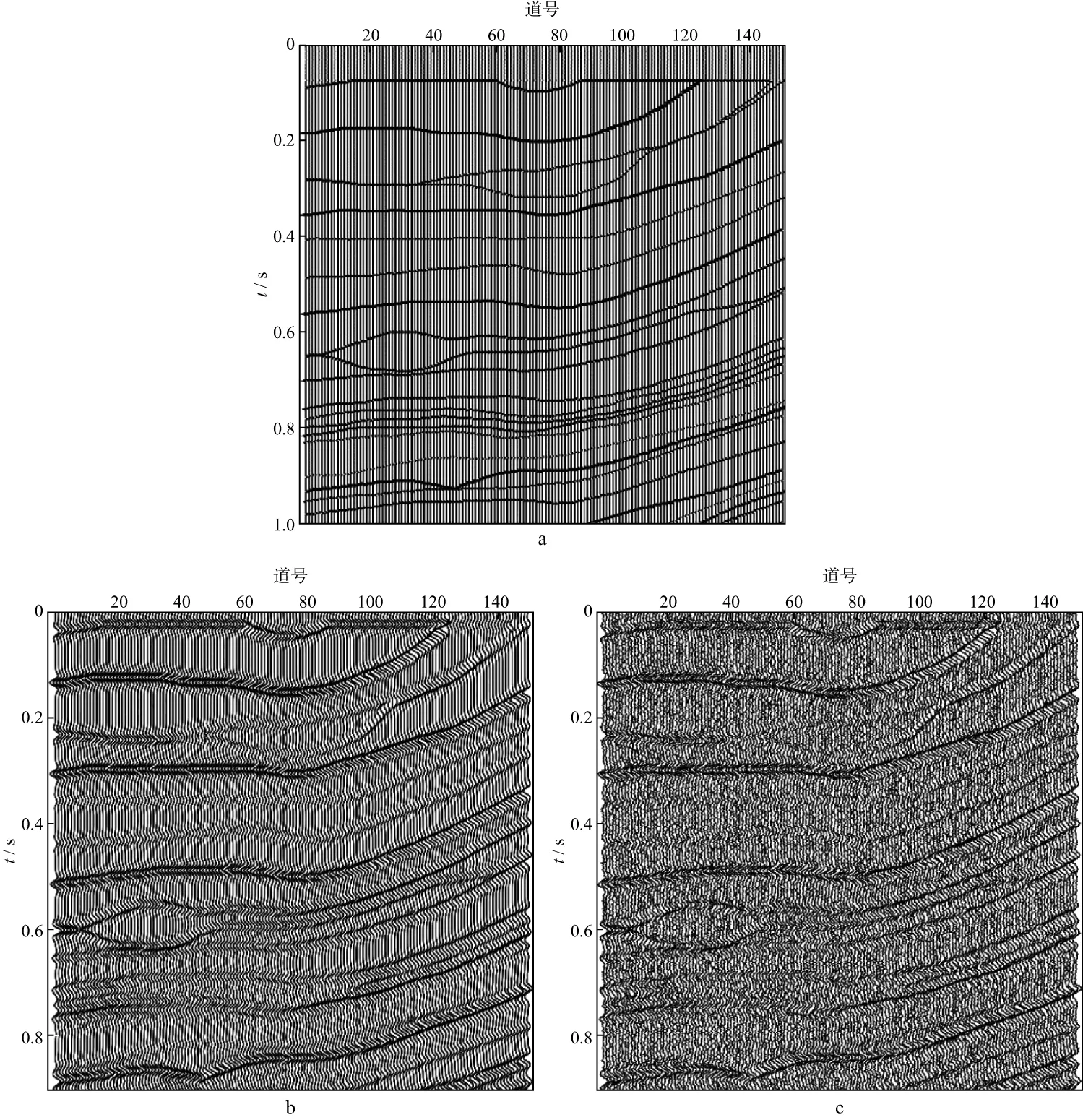


3 实际数据测试


4 结束语
