一种基于改进快速扫描法的多尺度近地表层析方法

蔡杰雄,王静波

(1.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103;2.中国石油化工股份有限公司勘探分公司,四川成都610041)

初至波走时易识别且稳定,在叠前偏移[1]、微震定位[2]等领域得到了广泛应用,尤其在复杂地区的初至波层析近地表建模[3-5]中得到了很好的应用。但在复杂、大数据地震勘探条件下,目前的初至波层析速度建模精度难以支撑静校正、真地表偏移等技术的实际应用。因此,提高初至波层析速度建模精度和效率迫在眉睫。

对于复杂工区的初至波层析,传统的弯曲法[6]和打靶法[7]计算效率低,且存在射线阴影区。VIDALE[8-9]基于波前面求解程函方程计算初至波走时,采用全局计算策略保证了计算的正确性,提高了计算效率,利用局部计算方法提高了计算精度和稳定性。在全局计算策略中,VIDALE[9]提出了盒式扩展法,计算效率高,但该技术无法适应地下介质速度剧烈变化情况;SETHIAN[10]提出了快速推进法(Fast Marching Method,FMM),通过模拟波前面并不断排序寻找走时最小的点向外计算,能够适应强变速介质,但极大地降低了计算效率;ZHAO[11]提出了快速扫描法(Fast Sweeping Method,FSM),在不同方向进行扫描,从而获得初至波走时在全空间的分布,该方法可以在任意维度进行计算,在局部计算方法相同的情况下,有效提升了计算效率[12]。在局部计算方法中,VIDALE[8]采用一阶差分格式;TRIER等[13]引入逆风有限差分法求解程函方程,以提高计算的稳定性;ZHANG等[14]和XIONG等[15]分别将差分格式扩展到三阶和五阶,以提高计算精度;ASAKAWA等[16]提出了线性插值法,采用线性插值和惠更斯原理计算局部走时;张赛民等[17]采用抛物型插值提高计算精度。但上述方法都没有结合波前扩展方法,引入了大量无用计算,影响计算效率。孙章庆等[18]利用“窄带”技术减少了无用的走时和射线信息计算,但是该技术需要排序,限制了方法的计算效率。

在反演方面,线性反演方法的主要思想是采用线性近似建立层析方程组,通过不断修改和迭代获得最终的速度模型。但是层析方程组数据量庞大且严重病态,难以保证计算的正确性和稳定性。另一种方法是基于局部最优化思想,通过对目标函数的局部线性化近似获得速度的修改方向与步长,然后通过迭代实现非线性反演问题的线性化求解。获得梯度的主要方法有伴随状态法[4,19]和散射积分法[20]。前者无需进行射线追踪,但其预条件在射线走时层析成像中不易实现;后者通过显式地计算核函数,并与走时残差向量相乘实现梯度的计算,但与传统的层析成像方法相同,散射积分法面临内存占用大的问题。李勇德等[21]充分利用矩阵元素的物理意义和Hessian矩阵的特性,在射线层析中引入了改进散射积分法[22],有效降低了层析过程中的内存占用;刘玉柱等[23]利用不同偏移距作为权函数提高浅层反演精度;刘小民等[24]将基于胖射线理论的初至波走时层析流程应用于叠前深度偏移。

为提高初至波层析的计算精度和效率,在正演方面,在传统快速扫描算法的基础上,提出基于改进快速扫描法的初至波走时计算方法;在反演方面,在改进散射积分算法的基础上,实现了多尺度反演策略。最后将提出的近地表建模方法应用于丁山工区实际资料处理,验证了方法的有效性。

1 改进的走时计算方法

1.1 基于双线性插值的局部计算方法

如图1所示,当A,B,C,D点的走时tA,tB,tC,tD已知时,需要计算点F的走时。为了简单起见,仅讨论网格间距(h)相等的情况。假设走时符合双线性假设(如图1所示,平面波在x,y两个方向上均为线性变化),则E1,E2,E点的走时tE1,tE2,tE可以表示为:

(1)

此时点F的走时可以表示为:

(2)

其中,s表示慢度。将公式(1)代入公式(2)可得:

(3)

根据费马原理,点F的走时是公式(3)的最小值,对公式(3)分别求x,y的偏导数并令其偏导数等于0可得:

(4)

方程(4)是一个走时计算的超越方程,没有解析解。张东等[25]采用网格界面剖分法求得固定节点上的近似解;刘锋等[26]通过最速下降法求得数值解;孙章庆等[18]利用平面波假设构造更简单的公式求得解析解。本文借鉴孙章庆等提出的方法进行求解。

图1 双线性插值法局部图解[18]

平面波先经过C点,然后经过D,B点到达A点,由平面波假设可得这4个点的走时方程:

tA-tD=tC-tB

(5)

则公式(4)化简为:

(6)

分析其单调性并整理得:

(7)

但是这种方法仅适用于平面波的情况,为了使其精度更高,在不符合平面波假设的区域可以利用一阶迎风差分格式进行计算。

为了考虑射线所有可能的方向,需要计算点F相邻的所有面元,但计算效率很低,可以采用迎风策略,选择射线最可能的方向进行计算。具体方法如下:

1) 假设点F的空间位置为(i,j,k);

2) 选择在z方向上靠近点F的两点中走时较小的为点A(如图1所示),其走时tA=min(ti,j,k+1,ti,j,k-1);

3) 选择在x方向上靠近点A的两点中走时较小的为点B(如图1所示),其走时tB=min(ti+1,j,Ak,ti-1,j,Ak),其中,下标Ak表示点A的z坐标;

4) 选择在y方向上靠近点A的两点中走时较小的为点D(图1),其走时tD=min(ti,j+1,Ak,ti,j-1,Ak);

5) 由点D和点B共同确定点C,其走时tC=tBi,Dj,Ak,其中,Bi表示点B的x坐标,Dj表示点D的y坐标;

6) 按照步骤2)到步骤5)的方法可以确定点F的走时值,比较该走时值与计算前的走时值,选取较小的值作为该点计算结果。

1.2 数值模型计算

为比较改进快速扫描法与传统一阶差分形式快速扫描法的优劣,本文分别将两种方法应用于简单均匀模型、复杂起伏地表模型。

1.2.1 简单均匀模型

模型大小为1000m×1000m×1000m,炮点位于(500m,500m,500m),网格间距为10m×10m×10m,采用1000m/s均匀速度。图2给出了在不同截面位置本文方法与传统方法的误差分布。由图2可见,本文方法零误差的范围和角度都好于传统方法。传统方法仅在水平和竖直方向误差较小,但本文方法在水平方向、45°方向和135°方向误差都较小。在计算效率不受影响的前提下,本文方法的最大相对误差降低为传统方法的48%,同时本文方法计算时间为0.82s,传统方法为0.83s,计算效率几乎没有改变。

1.2.2 复杂起伏地表模型

图3给出了2.5维起伏地表Marmousi模型,模型大小为7450m×1000m×3000m,网格间距为25m×10m×10m,炮点位于(2500m,500m,0)。共5条接收线,线间距200m。每条测线检波器x坐标最小为1250m,最大为6250m,道间距25m。图4a为采用本文方法得到的y=500m处的走时等值线,在起伏地表情况下,本文方法计算结果没有出现奇异值,且正常产生了回转波,说明本文方法适应起伏地表复杂速度模型。

为了提高计算效率,仅计算炮检距范围内地下2000m深度内的走时,结果如图4b所示。本文方法计算全部走时场需4.21s,计算2000m深度范围走时场需3.36s,传统方法计算全部走时场需6.11s,本文方法计算时间为传统方法的55%。需要注意的是,计算范围的选择应该根据实际情况确定,否则会影响回转波和折射波的产生。

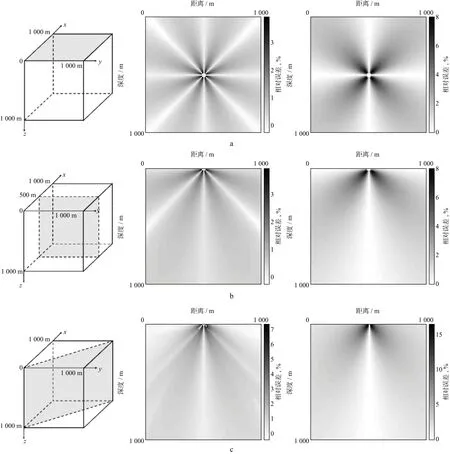
图2 不同截面位置本文方法(左)与传统方法(右)的相对误差分布a z=0; b x=500m; c x=y

图3 2.5维起伏地表Marmousi模型

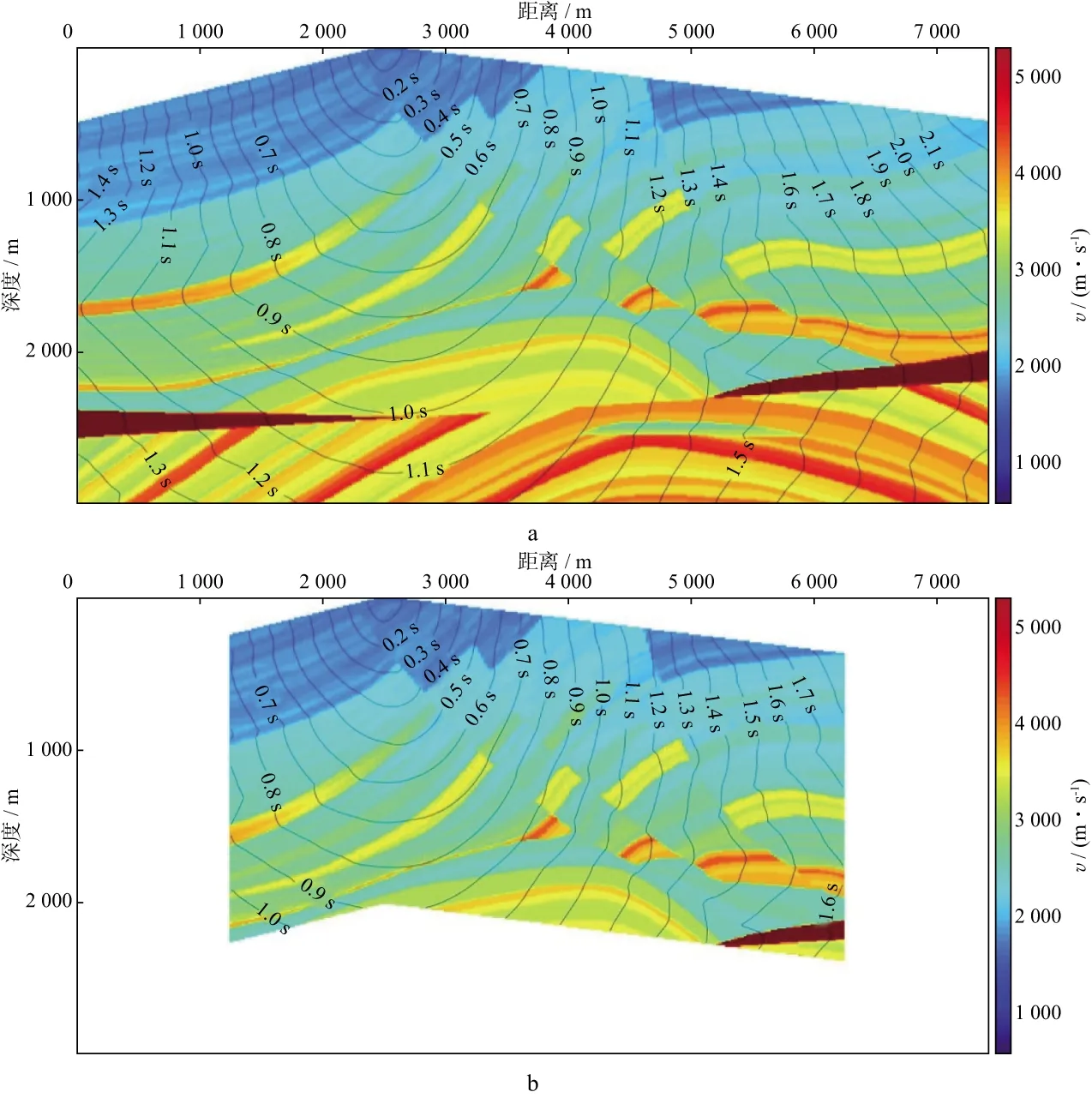
图4 采用本文方法得到的y=500m处的全局(a)与部分(b)速度模型与走时等值线

2 多尺度改进散射积分法走时层析

2.1 改进散射积分法预条件最速下降方向计算

初至波走时层析通过计算走时与拾取走时的差计算出模型修正量,不断迭代逼近真实模型。假设某个模型空间大小为m,数据空间大小为n,根据走时与慢度的关系可以建立走时矩阵:

Ks=t

(8)

其中,K为走时层析中的敏感核函数(Fréchet导数矩阵),其规模为n×m,s为空间慢度向量,t为初至波走时向量。对公式(8)进行线性近似可以获得慢度的修正量与走时差之间的关系:

KΔs=Δt

(9)

建立预条件最速下降方向迭代公式:

sl+1=sl+αlpl

(10)

式中:αl表示第l轮迭代的步长;pl表示第l轮迭代的梯度;sl表示第l轮空间内各点的慢度。

(11)

p=(KTK)-1KTΔt

(12)

其中,Ha表示Hessian矩阵。改进的散射积分法[21]将(12)式中的KTΔt和KTK表示为多个向量-标量乘积的累加运算,由于(KTK)-1主对角线占优,这里用其对角线H0代替。为了避免由于对角元素中存在很小的数而导致的不稳定性,需要引入正则化项,所以最终的梯度为:

p=(H0+λI)-1KTΔt

(13)

其中,I表示单位矩阵,λ表示一个较小的数。将(13)式代入(10)式,即可实现预条件最速下降法初至波走时层析。

2.2 多尺度层析策略

对于地下介质速度随深度线性增加的初始模型,地下深度z处的速度可以表示为v=v0+βz,射线可以达到的最大深度h可以表示为:

(14)

其中,v0表示地表速度,β表示速度梯度,h表示深度,x表示最大炮检距。可以发现,当使用同一梯度模型作为初始模型进行初至层析建模时,随着偏移距的增大,射线可以达到的深度也随之增大;对于同样偏移距,随着速度梯度的增大,射线达到的深度也随之增大。

鉴于射线必须经过近地表浅层,在更新过程中会模糊浅层细节,所以在深层更新结束后逐步减小最大炮检距,刻画浅层速度模型,实现反演深度的多尺度策略。为了建立更高精度的速度模型,采用先深后浅的反演策略,先用全炮检距数据进行层析,更新近地表深层信息。由于高频假设,射线层析集中在一条没有宽度的“线”上,层析矩阵大量零元素会导致反演不稳定,为此,采用较大的网格减少反演的不稳定性,并随着迭代次数的增加,逐步减小网格大小来提高精度,实现反演精度的多尺度策略。这种反演深度与反演网格同时变化的多尺度建模策略能有效提高速度建模精度与稳定性。

2.3 理论数据测试

采用SEG起伏地表SEAM模型数据对本文方法进行了测试,图5为y坐标6500m处的真实速度模型。该数据x,y,z方向网格采样点分别为1447,1250,800个,网格大小均为10m。起伏地表上部填充的速度为340m/s。观测数据是高精度弹性波模拟数据的初至拾取结果。

图6为y坐标6500m处全偏移距层析反演的速度模型。可以看出,通过改进散射积分法初至波走时层析可以获得平滑的背景速度。为了提高反演分辨率,采用多尺度反演策略,即随着迭代次数的增加,输入的最大偏移距分别为4000,2000,1000和500m,网格大小分别为100,50,20,10m。每一个反演参数内部迭代20次。抽取y坐标为6500m处的剖面进行分析。图7为反演的速度模型,可以看出,多尺度反演策略增加了近地表的高频成分。图8对比了不同位置纵向抽取的速度函数,可以看出,采用分偏移距反演策略之后,浅部的反演精度得到了有效提高。

图5 y坐标为6500m处的真实速度模型

图6 y坐标为6500m处全偏移距反演的速度模型

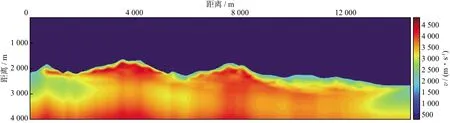
图7 y坐标为6500m处分偏移距反演的速度模型

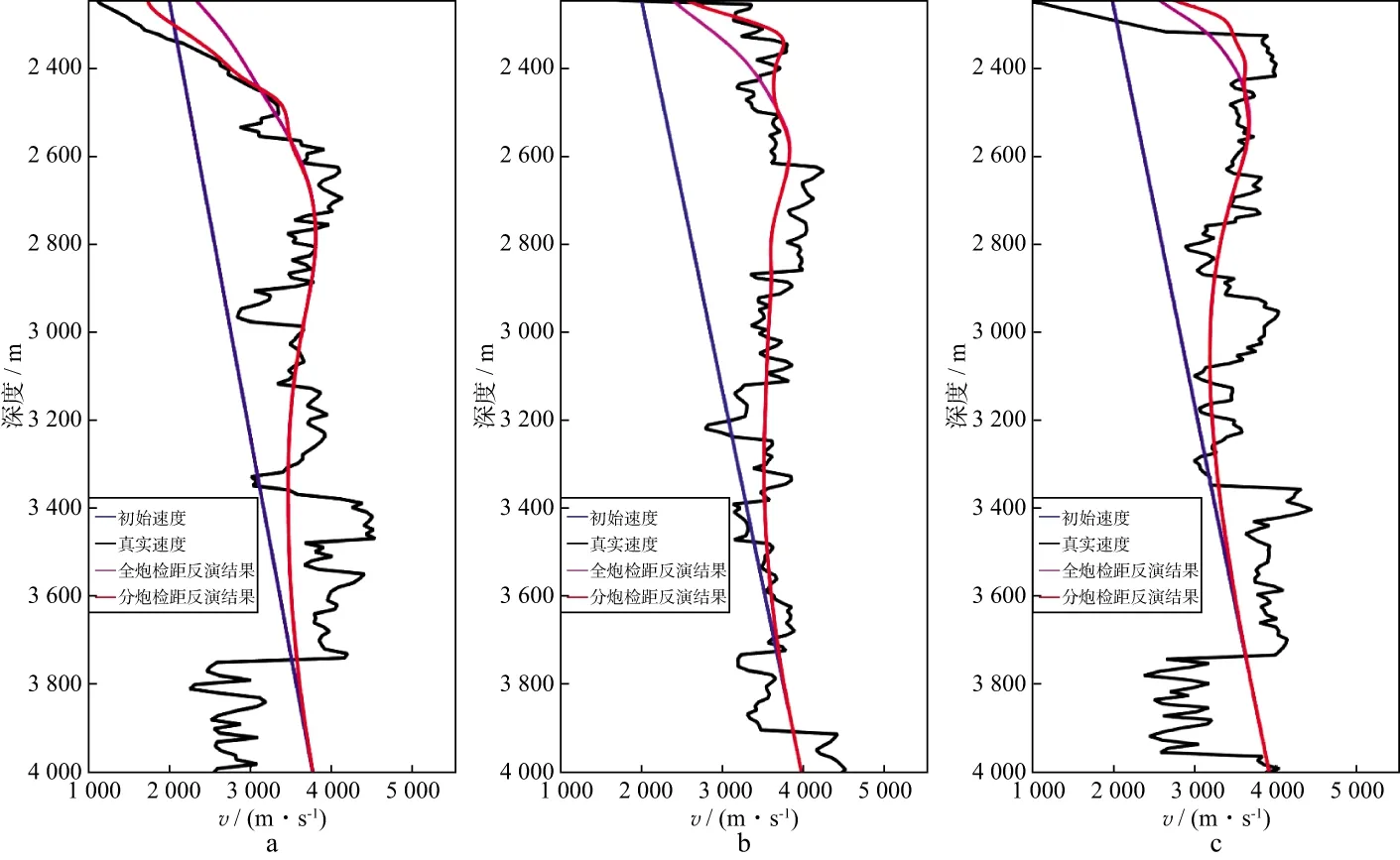
图8 不同位置纵向抽取的速度函数a x坐标为5000m,y坐标为6500m; b x坐标为7000m,y坐标为6500m; c x坐标为9000m,y坐标为6500m

3 实际应用

丁山工区为复杂山地页岩气勘探区,地表起伏剧烈,高速岩体出露地表,导致地表横向速度变化快。前期处理采用常规初至波层析方法,得到的最终单炮初至走时拟合平均误差达30ms(图9),严重影响后续偏移成像精度,导致较大的井震误差,达不到页岩气勘探水平井钻探对成像精度的要求。为此,在该工区采用本文方法进行了近地表速度建模。输入的最大偏移距分别为全炮检距,4000,2000和1000m,网格大小分别为400,200,100和100m,每一个反演参数迭代25次。该单炮的初至波走时拟合平均误差为11.2ms,降低到以前误差值的37.33%,说明本文方法建模精度更高。图10为利用传统方法和本文方法得到的INLINE 2400线速度模型,可以看出,与传统建模方法相比,本文建模方法获得的速度模型近地表信息更加丰富,速度横向变化更加剧烈。图11为采用传统方法和本文方法建模的偏移结果,可以看出,利用本文方法建立的近地表速度模型,偏移结果更加清晰,层位更加连续(图11中黑圈所示)。

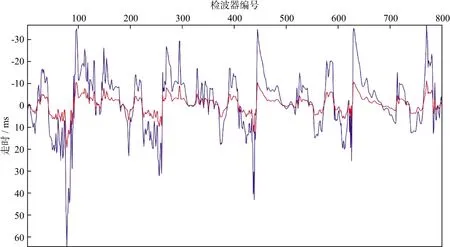
图9 某单炮传统方法建模(蓝线)与本文方法建模(红线)走时误差对比

图10 INLINE 2400线采用传统方法(a)与本文方法(b)建模得到的速度模型对比

图11 INLINE 2400线采用传统方法(a)与本文方法(b)建模的偏移结果对比

4 结论

本文从正演和反演两个方面对初至波走时射线层析进行了改进。正演方面引入双线性插值技术,有效提高了快速扫描法的计算精度,同时保持了该方法计算效率高的优势;反演方面采用多尺度策略,有效提高了改进散射积分法层析反演精度。理论模型数据测试结果表明,本文的正、反演方法可以有效提高近地表建模精度。丁山工区近地表速度建模精度的提高有效改善了成像质量,说明了本文速度建模思路的有效性和可行性。

本文方法基于射线理论,计算精度不易再进一步提升,下一步应逐步开发依托波动理论的近地表建模方法,充分挖掘初至波振幅、相位等信息,进一步提高近地表建模精度。