基于机器学习的冠心病住院费用预测研究

夏涛 徐辉煌 郑建立

摘 要：冠心病是一种常见的心血管疾病，具有高发病率的特点。因此，冠心病住院费用的预测对于控制医疗费用有着重要意义。本文基于机器学习方法，通过将总的住院费用划为8个分项费用，以患者特征作为输入，结合随机森林与极端梯度提升算法，并使用十折交叉验证确定最佳的分项费用预测模型。再根据分项费用的预测值进行求和得出总的预测住院费用。总费用预测模型的拟合优度（R2）为0.825，平均绝对百分比误差（MAPE）为29.16%。以此预测模型测试新的数据集，结果R2为0.769，MAPE为29.13%。结果表明，本文建立的费用预测模型能够有效地预测冠心病住院费用。

关键词： 冠心病;住院费用;集成学习;随机森林;极端梯度提升

【Abstract】 Coronary heart disease is a common cardiovascular disease characterized by high morbidity. Therefore， the prediction of hospitalization expenses for coronary heart disease is of great significance for controlling medical expenses. Based on the machine learning method， this paper divides the total hospitalization cost into eight sub-items， takes the patient characteristics as input， combines the Random Forest and extreme gradient boosting algorithm， and uses the ten-fold cross-validation to determine the best sub-cost prediction model. Then， the total predicted hospitalization expenses are obtained by summing the predicted values of different itemized expenses. The total cost prediction model has a goodness of fit （R2） of 0.825 and an average absolute percentage error （MAPE） of 29.16%. Using this predictive model to test the new data set， the result is R2 of 0.769 and MAPE of 29.13%. The results show that the cost prediction model established in this paper can accurately and effectively predict the hospitalization cost of coronary heart disease.

【Key words】  coronary heart disease; hospital costs; ensemble learning; Random Forest; extreme gradient boosting

0 引 言

2017年，國务院印发《关于进一步深化基本医疗保险支付方式改革的指导意见》等系列政策文件，针对医保支付方式提出了明确的指导意见，疾病诊断相关分组[1]（Diagnosis-related groups， DRGs）收付费改革在全国多地医院开展试点。DRGs是以出院患者信息为依据，综合考虑患者的主要疾病诊断以及治疗方式，并结合患者体征如年龄、并发症和合并症，将疾病的复杂程度和费用相似的案例分到同一组，从而让不同强度和复杂程度的医疗服务之间有了客观对比依据。

随着老龄化进程的加速，中国冠心病的患病率和死亡率呈现上升趋势。本文基于DRGs收付费方式，探究如何在冠心病患者入院时根据患者的不同情况如性别、年龄、疾病的严重程度、手术与否等来预测出患者的总费用，并将总费用控制在相应的DRGs分组[2]中，由此达到对医疗费用的有效控制。费用预测使医疗成本趋近于合理，从而保证医疗质量，提高医院竞争力。另外，费用的预测能够为住院处收取预交金提供数据参考。

近年来，随着机器学习技术的发展，基于机器学习的疾病医疗费用预测成为研究热点之一。宋振等人[3]采用人工神经网络模型来对胆石病患者住院费用因素进行分析，得到住院天数、医院等级、结石部位、是否手术等对住院费用均有影响。张继[4]使用决策树分类算法对妇科肿瘤患者住院费用做了一定的研究，得出妇科恶性肿瘤患者住院费用的影响因素，包括入院诊断、年龄、婚姻、住院天数、入院情况、出院情况、手术方式以及麻醉方式。赵璇[5]采用决策树算法分析了影响患者医疗费用的因素，得到住院天数、药品使用规则、卫生材料使用、就诊医院等不同因素会影响冠心病患者费用。郭伟文等人[6]应用灰色GM（1，1）模型预测住院费用，得到人均住院费用模型的平均相对误差为2.36%。

上述研究通过不同的数据挖掘算法对影响费用的因素进行定量分析，但是没有对相应的住院总费用加以预测。使用灰色GM（1，1）模型预测住院费用只是基于统计学原理对费用进行粗略的预测，缺乏实用性和参考性。

本文采用机器学习中的集成学习方法建立冠心病住院费用的预测模型。首先采集2017～2019三年的冠心病患者信息以及相应的住院费用数据，对数据进行预处理和特征选择，将得到的特征作为输入。其次，使用4种机理不同的机器学习算法对冠心病住院患者治疗总费用中占比最大的材料费用进行预测性能比对，并确定最佳回归器。针对2017～2018两年的冠心病住院的分项费用建立了8个回归器，并进行十折交叉验证。将所有分项费用预测值求和后与实际总费用进行比较，使用拟合优度和平均绝对百分比误差作为度量指标，由此确定最佳的费用预测模型。最后，应用此模型对2019年的冠心病治疗费用进行预测。预测结果稳定，证明了本文方法的实用性和有效性。

1 材料与方法

1.1 数据选取与预处理

本文数据来源于某三甲医院数据库，通过文献阅读，从医院信息系统（HIS）数据库和临床信息系统（CIS）数据库中抽取冠心病住院患者信息和费用信息。冠心病患者的信息可以从人口学特征、临床因素、管理因素、支付方式等因素抽取，费用信息可以从结算日期、每一部分的费用明细等提取。

抽取患者信息和费用信息时，数据会存在异常值、缺失值、错误值、重复记录等问题，需要进行数据预处理，如删除住院天数小于1天或者大于1年的住院记录等异常值。处理空值（NULL）则应对缺失值进行补充或删除该变量[7]。如果该变量缺失值大于总样本数目的1/3，就删除该变量;若该变量的缺失值低于样本的1/3，则根据其他信息对该变量进行相应的补充。通过数据预处理，数据总共有7 200份样本，将2017～2018年5 800份作为训练集，2019年1 400份作为测试集。

1.2 特征处理

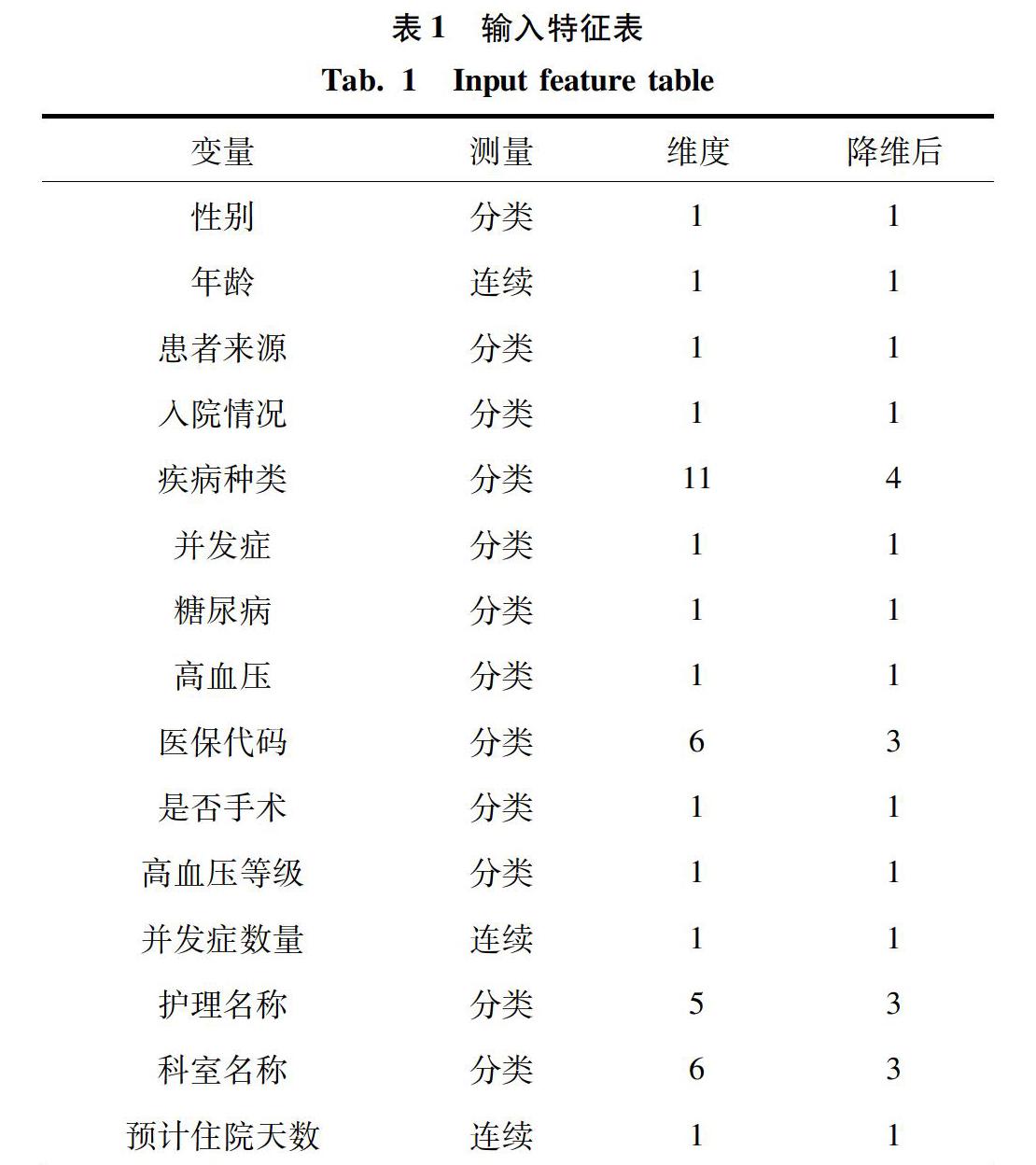
数据预处理后，需要选取更加精确、有意义的特征作为模型训练的特征向量。经查阅相关文献并结合医院数据库的有效信息，本文选取的特征见表1。在回归建模中，分类特征不应直接使用，需要进行独热编码[8]使其特征得以数字化。离散型特征独热编码后，能使得特征向量之间的距离计算更加合理。本文中“护理名称、疾病种类、医保代码、科室名称”特征都属于离散特征，应对其进行相应的独热编码。

多类别特征独热编码后映射到高维的特征空间，稀疏性会增多。稀疏特征会影响或误导学习器，因此，需要通过降维删掉冗余特征只保留主成分。本文采用SparsePCA[9]进行数据降维，通过机器学习开源库Sklearn[10]的decomposition.SparsePCA函数来实现。

对疾病种类特征进行独热编码后，SparsePCA函数的n_components（返回的特征数目）设置为4，而科室名稱、护理名称和医保代码的n_comonents设置为3。参数的设置旨在最大程度保留有效信息，减少稀疏分量。经过降维，科室名称降至3维，护理名称降至3维，医保代码降到3维，疾病种类降到4维。结合性别、年龄、入院情况、患者来源、是否手术、高血压等级、是否患有高血压、是否患有糖尿病、是否并发症以及并发症的数量，共24维特征构成回归器的特征输入。

1.3 基于集成学习的住院费用预测建模

机器学习中处理回归问题主要分为两大类。一类是广义线性回归算法，另一类是集成学习方法。其中，集成学习使用一系列学习器进行训练，运用某种规则把各个预测结果通过整合来获得比单个学习器更好的学习效果。集成学习相比广义线性回归优势在于保证模型的准确度，并可有效防止模型过拟合，具有较高的鲁棒性。本文将住院总费用拆分为8种费用类别，包括：检验费用、材料费用、治疗费用、住院费用、药品费用、护理费用、手术费用与其他费用。

1.3.1 随机森林

1.3.3 总住院费用预测建模

本文通过对特征进行处理，将上述24维特征作为回归器输入，并使用集成学习方法，结合十折交叉验证建立总住院费用预测模型。

总的住院费用是由检验费用（jyfy）、材料费用（clfy）、药品费用（ypfy）、治疗费用（zlfy）、护理费用（hlfy）、手术费用（ssfy）、住院费用（zytsfy）、其他费用（qtfy）构成。因此，通过对其子项费用进行预测后求和可得到总预测住院费用。

分析可知，材料费用占总住院费用的比重最大，该模型预测精确与否会极大影响总费用模型的性能。因此，在建立材料费用的预测模型时采用Lasso回归、K近邻回归（KNN）、支持向量回归（SVR）、随机森林与XGBoost多种机理不同的算法进行比较，拟合优度分别为0.821，0.549，0.659，0.824，0.826，确定XGBoost为材料费用的最佳预测模型。

对于材料费用之外的分项费用，由于其数值所占的比重较低，所建立的不同费用回归器的预测精度对总费用预测模型的影响较小。子项费用回归器越简单，聚合而成的总费用预测框架就越稳定。此外，随机森林需要调试的超参数少于XGBoost，以此构建的预测模型复杂度比XGBoost低。因此，为保证预测框架的鲁棒性，本文运用随机森林对其它子项费用进行预测建模。

总费用预测模型的流程如图1所示。在对子项费用建立回归模型时，采用网格搜索确定各个模型最佳参数，随机森林模型参数见表2。

材料费用的XGBoost模型最大深度为3，学习率为0.01，集成树数目为600，最小子节点权重为5，训练样本子采样率为0.8，特征列采样率为0.8，L2正则化项为1。

2.3 特征权重分析

本文将总费用拆分为8项子费用，在分别建立费用预测模型后，计算出每个模型不同特征的重要性，并取7个特征度最大的预测变量制图，详见图2。

从图2可知，住院天数特征对治疗费用模型、住院费用模型、护理费用模型、其它费用模型以及药品费用模型影响较大。是否手术特征对材料费用模型、手术费用模型影响较大。这对后续费用控制的研究有一定指导意义。

3 结束语

对冠心病住院费用的控制能减轻患者负担，降低治疗成本，提高医疗质量，因此费用预测具有研究意义。本文基于机器学习中的集成学习方法，根据24维特征输入构建出不同回归器，并对冠心病住院患者的分项费用进行预测，确定了结合随机森林和极端梯度提升的费用预测模型，而且通过拟合优度和平均绝对百分比误差度量模型的预测性能。

实验结果显示，本文构建的费用预测模型能够有效预测冠心病住院费用。后续工作将采集更多的数据完善模型，进一步优化算法，提升预测性能，并应用到疾病费用预测工具当中。

参考文献

[1]唐剑， 陈武朝， 王桂榕. 疾病诊断相关分组（DRGs）研究及应用[J].中国病案， 2014， 15（5）： 36-39.

[2]杨超. 面向诊断分组的费用预测研究和实现[D]. 成都：电子科技大学， 2017.

[3]宋振， 李长平， 崔壮， 等. 基于人工神经网络模型的胆石病参保患者住院费用分析[J].中国预防医学杂志， 2013， 14（1）： 31-34.

[4]张继. 基于数据挖掘技术的妇科肿瘤病人住院费用研究[D]. 郑州：郑州大学， 2011.

[5]赵璇. 基于数据挖掘技术的冠心病费用研究[D]. 北京：北京中医药大学， 2018.

[6]郭伟文， 梅文华， 郭文燕. 应用灰色GM（1，1）模型预测医院住院量和住院费用[J].中国病案， 2018， 19（11）： 62-66.

[7]李汝庆. 基于数据挖掘技术对精神科病人住院天数的预测[J].电子世界， 2015 （17）： 143-145.

[8]梁杰， 陳嘉豪， 张雪芹， 等. 基于独热编码和卷积神经网络的异常检测[J].清华大学学报（自然科学版）， 2019，59（7）：523-529.

[9]ZOU Hui， HASTIE T， TIBSHIRANI R. Sparse principal component analysis[J]. Journal of Computational & Graphical Statistics， 2006， 15（2）：265-286.

[10]PEDREGOSA F， VAROQUAUX G， GRAMFORT A， et al. Scikit-learn： Machine learning in Python [J]. Journal of Machine Learning Research， 2012， 12（10）： 2825-2830.

[11]BREIMAN L. Random Forests [J]. Machine Learning， 2001， 45（1）： 5-32.

[12]王鹏新，齐璇，李俐，等.基于随机森林回归的玉米单产估测[J].农业机械学报，2019，50（7）：237-245.

[13]CHEN T， GUESTRIN C. XGBoost： A scalable tree Boosting system[C]//ACM SIGKDD International Conference on Knowledge Discovery & Data Mining.San Francisco， CA， USA： ACM， 2016：785-794.

[14]施国良， 景志刚， 范丽伟. 基于Lasso和Xgboost的油价预测研究[J]. 工业技术经济， 2018， 37（7）： 31-37.