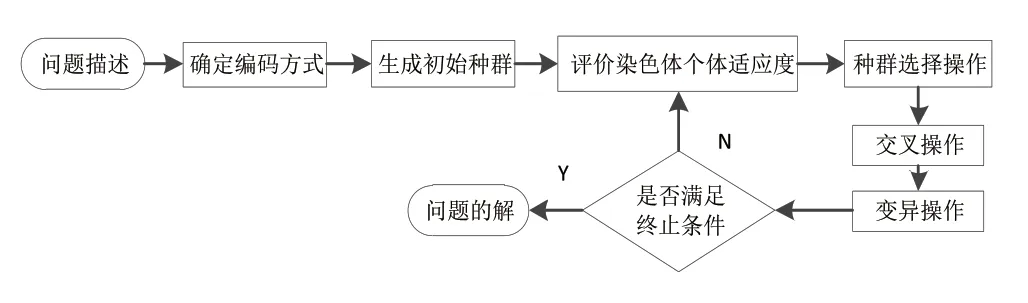
基于遗传算法的自动化立体车库库位分配
2019-12-05陈桢,杨旻
陈 桢,杨 旻
(1.上汽大众汽车有限公司 上海,201805;2.壳牌(中国)有限公司,上海 200336)
0 引言
随着我国汽车保有量越来越高,停车日益困难,自动化立体车库容量大、占地面积少、停车方便,是解决停车问题的一个有效方法[1],常见的自动化立体车库有升降横移式、巷道堆垛式、垂直升降式、垂直循环式等[2],近年来出现了许多新型立体车库,例如仓储平面移动式停车设备,其特点是车库密度高、安全可靠、自动化程度高、具有自动对中装置、存取车效率高[3]。随着立体车库的发展,有很多学者研究其存取车策略[4],由于各种立体车库的结构及选取目标函数的不同,各种存取车策略在实际的应用中有许多的不同点。
常见的立体车库存取车策略研究大多针对只有一个升降机的自动化立体车库,如李剑锋等人利用改进遗传算法研究了巷道堆垛式立体车库调度策略[5];鲁立等人对出入库的策略提出了一种基于社会最小等待时间的出入库优化算法,将其应用于存取车优化[6];孙军艳等人利用改进的交叉算子遗传算法对三种不同库容的升降横移式与巷道堆垛式立体车库进行存取车调度优化[7]。
本文的研究对象是具有两台汽车升降机的存取分离式仓储平面移动式立体车库,相对于只布置一台汽车升降机的仓储平面移动式立体车库,其整体用户存取车等待时间更短。由于在车库的结构确定的情况下,存取车由升降机和搬运机完成,因此车库的存取车效率与存取策略有密切的联系,本文将针对具有两台升降机即具有单独的入库口和出库口的立体车库进行存取车策略优化并比较各策略的存取车效率。
1 立体车库结构
本文所研究立体车库的结构如图1所示,其中1~3层为SUV等大型汽车存放区,4~9层为中小型汽车存放区。左右分别设置两台汽车升降机,每台升降机配备一台汽车搬运器。在本立体车库中若进行存车任务,则控制系统控制1号升降机开门,汽车驶入升降机内的搬运器,等待驾驶员及乘客离开。升降机根据控制系统分配的具体车库位置停到对应的楼层。搬运器连同车辆从升降机内离开,运输汽车到指定位置后,返回升降机内,升降机1返回初始位置。若执行取车任务,汽车升降机2升到对应楼层,搬运器从升降机内离开将汽车取出后运入升降机,升降机降至出口,等待驾驶员将车辆开离即完成取车。

图1 立体车库示意图
2 库位分配策略设计
在进行车辆存取的过程中,控制系统需要为每一辆进入车库的汽车分配库位,目前常用的库位分配方法为自然排序存取法、存车优先策略和取车优先策略:自然排序存取法对车库的所有库位依次编号,并对当前空余的库位统计并排序,依次配对给的需要存车的车辆[8]。取车方法类似,查询到客户车辆存放的实际库位编号,而后依次执行取车操作。这种传统存取模式优点是简单可靠,控制系统简单,缺点是车库存取效率不高;存车优先策略即将汽车放在楼层较低且靠近入口处的库位;取车优先策略即将车存在楼层较低靠近出口处的库位,这两个目标在汽车存放位置上存在矛盾;同时本车库采用会员制,会员等级越高,其车辆的存取车优先级越高。
因此综合用户存车体验及现场存车秩序,本文设计的自动化立体车库库位分配策略如下:
1)用户存取车:存车时用户按照到达车库的先后顺序将汽车开入升降机后离开,取车时用户按照启动取车任务的先后顺序将汽车从升降机开走完成取车。
2)库位楼层分配:1~3层大型车辆存放区和4~9层中小型车辆存放区在库位分配时相互独立。即若下一辆要存放的轿车为中小型车辆,则只考虑4~9层的库位。
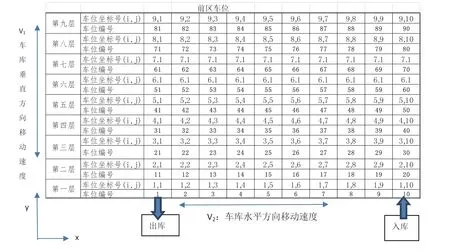
图2 平面立体式立体车库二维坐标图
3)库位分配:考虑存车优先、取车优先以及车库用户会员制,本文设计一种策略可调的自动化立体车库库位分配方法。在有大量汽车需要入库的时采用存车优先策略,快速存车,缓解车库入口拥堵情况;在正常情况下采用取车优先策略,将车辆停放在出库口附近,减少出库时间同时将靠近入口的库位空出来以备存车集中时减少存车等待;会员等级高的用户无论是在存车优先还是取车优先的策略下,其汽车存放位置都需要相对靠近出口,以减少会员取车等待时间。
3 库位分配策略实现
3.1 数学模型建立
为实现,上述库位分配策略,本文以最小化总出库、入库时间为目标分别建立数学模型,为便于建立系统数学模型,现做出如下设定:
1)本仿真过程中所有需要存放的车辆均为中小型汽车,即本文只以4~9层为例进行库位分配,1~3层的库位分配方法与4~9层类似;
2)由于本车库前后为对称结构,所以本文只考虑4~9层的前区库位,库位编号如图2所示,后区库位分配方法与前区类似;
3)在整个仿真过程中,立体车库运行正常,不考虑其余非正常影响因素;
4)设某时刻共有Nm辆车需要入库,共有Ns个空余库位,若Nm>Ns,则取Nm=Ns,剩余未能被分配的汽车放到立体车库后区空余库位上分配。
建模过程中的相关变量设定如下,设库位坐标号为(i,j),i为楼层号,j为库位列号;设升降机沿y轴的平均运行速度为v1,搬运器沿x轴的平均移动速度为v2;库位在x轴方向的宽度为s,1~3层的平均层高为h1,4~9层的平均层高为h2;设司机将车驶入/驶出汽车升降机的时间为T0,搬运器从汽车升降机移出或移入的时间为T2,搬运器将车辆存入/取出库位的时间为T3。
3.1.1 存车优先模型
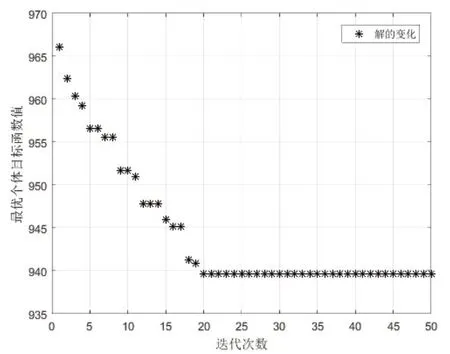
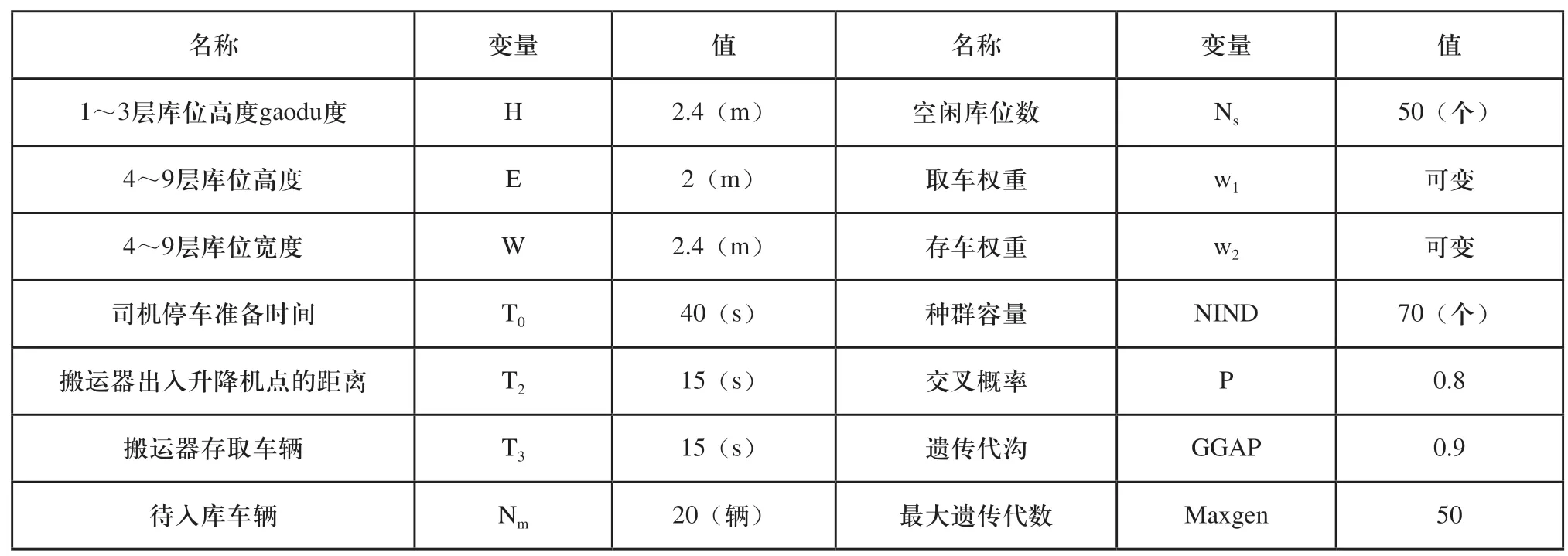
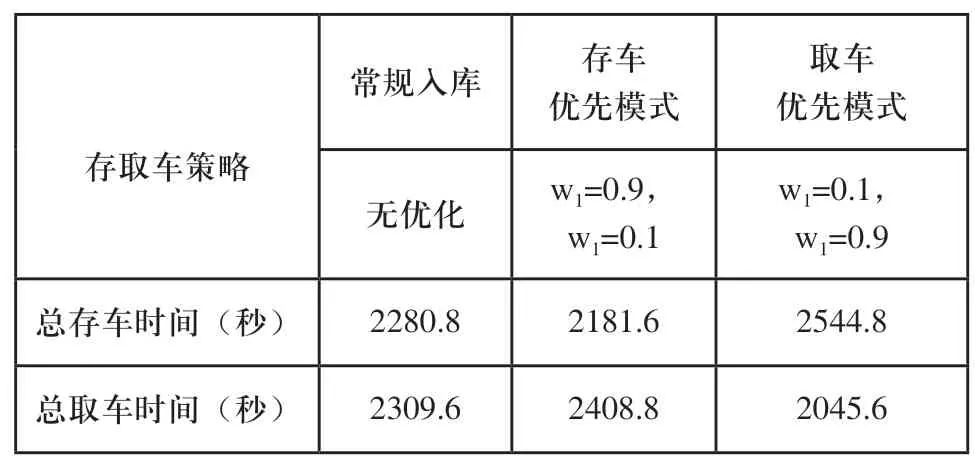
只考虑某时刻的存在的Nm辆需入库车辆,存车优先策略要求存车所需要的总时间最短。编号为k的车辆要存到(i,j)(i>3,0 将Nm辆车全部存入立体车库所需要的时间如式(2)所示。 存车优先策略的目标函数即如式(3)所示。 式中,GI为最少总存车时间,s。 3.1.2 取车优先模型 取车优先策略要求将所有待取车辆从车库取出所需要的总时间最短。设编号为k的车辆要从(i,j)(i>3,0 将Nm辆车全部取出所需要的时间如式(5)所示。 取车优先策略的目标函数即如式(6)所示。 式中,GO为最少总取车时间,s。 3.1.3 会员制度模型 会员制度即为把会员等级高的用户车辆停放在相对同一批入库车辆更靠近出库口的位置,这个目标可以与出库优先策略合并。若某车的VIP等级为u,则参考会员制度的出库优先目标函数可以表达如式(7)所示。 VIP等级越高,u的值就会越大,Pk被放大的倍数越大,这辆车的取车时间相对于其他VIP等级低的用户对总取车时间的影响就会越大。为了降低取车总时间,只能尽量减少Pk的值,即会把该VIP等级高的车停放的越靠近出口。 3.1.4 系统数学模型 综合考虑以上因素,为实现在库位分配过程中能够根据实际情况灵活调整库位分配策略的需求,本文采用权重系数法来建立系统数学模型,将权重w1分配给存车优先模型,将权重w2分配给综合了会员制度的取车优先模型,有大量车辆需要入库时,增大权重w1,正常情况则增大权重w2。则若将Nm个车辆存入车库,则库位分配的系统数学模型如式(8)所示。 遗传算法借鉴生物进化的过程来解决问题,在种群中通过交叉、变异等操作逐步找到更优的解,并淘汰较差的解,多次进化后得到近似最优解[9],其计算过程如图3所示。 图3 遗传算法计算过程 3.2.1 染色体编码与解码 编码是遗传算法设计的关键步骤之一,它是解空间与问题空间转换的桥梁,编码方式直接影响遗传算法的运算结果。目前常用的编码方式有实数编码、二进制编码、浮点数编码等。 本文采用浮点数编码将待入库车辆与遗传算法的染色体结合,设有Ns个空闲库位(n1,n2,n3,……,nNs)和Nm个待入库的车辆(m1,m2,m3,……,mNm),经过选择交叉变异后得到一条浮点数组成的染色体(β1,β2,β3,……,βNs),该染色体与空闲库位一一对应,即βi对应库位ni,将库位按照其对应β_i的数值从小到大排序,取前Nm个库位分别对应于待入库车辆。举例说明:此时共有6个空闲库位[15,16,18,25,29,57]和5个要入库的车辆[1,2,3,4,5],这五辆车的VIP等级为[0.56,0.12,0.32,0.86,0.19],若有一条染色体G=[0.4,0.7,0.03,0.1,0.21,066],即基因0.4对应15号库位、0.7对应16号库位……以此类推。将库位按照G排序后得到[18,25,29,15,57,16],即1号车辆存入18号库位,2号车辆存入25号库位,以此类推,而后根据车辆的VIP等级及其对应的库位去计算该条染色体的适应度信息。 3.2.2 遗传运算 本文使用MATLAB的遗传算法优化工具箱,在选取下一代个体时,采用轮盘赌选择法,代沟值设为0.9,在产生新个体时使用单点交叉。本文给定最大遗传代数Maxgen,当遗传运算次数等于Maxgen后,停止运算并输出适应度最优的个体,通过多次的运算发现,设最大遗传代数为30代完全能够得到系统的最优解,如图4所示,这里为留有一定的余量设最大遗传代数为50代。遗传算法优化过程如下: 1)设定基本参数值,选择权重w1和w2的值,最大遗传代数为50,遗传代数初始值为1,种群容量为70; 2)根据空闲库位的数量设定染色体的长度,按照浮点数编码产生70条染色体,作为遗传算法的初始种群; 3)根据编码方式解码出每条染色体对应的库位排列信息和车辆信息,根据式(8),计算每条染色体的适应度; 4)按照适应度对染色体进行排列,根据代沟值使用轮盘赌选择染色体,并对未被选中的染色体进行交叉操作得到新的染色体,重新组成下一代种群; 5)遗传代数加一,并判断是否达到了最大遗传代数,如果达到了则输出目前适应度函数最低的那条染色体,对这条染色体进行解码,得到库位分配信息;若未达到则返回步骤3)继续计算。 图4 遗传算法收敛情况 本文对立体车库的存取策略进行了三种分析,假定现在4~9层的立体车库60个库位,已经在编号为[37,43,45,47,61,67,73,75,87,88]的库位上存放了10辆车,有20辆车需进行空余库位分配,且其VIP等级按照序号排为[0.13,0.29,0.17,0.02,0.33,0.88,0.25,0.37,0.38,0.01,0.95,0.85,0.15,0.45,0.23,0.25,0.52,0.67,0.99,0.33]。计算过程中其余相关参数设置如表1所示。 按照表1所述参数取不同的权重值进行遗传算法求解,得到如下结果。 1)w1=0.9,w1=0.1 按照上述权重值即存车优先,得到的库位分配结果如图5中蓝色色块所示,色块内数字代表入库车辆的编号,即1号汽车分配在42号库位,2号汽车分配在33号库位……以此类推,可看到这20辆车的库位分配情况为存车优先时车辆存放位置多集中在入口处,并且VIP等级较高的6号、11号、12号、18号车及19号车相对靠近车库出口。 2)w1=0.1,w1=0.9 取上述参数即为取车优先,算法的收敛情况与上述情况类似,这里不再赘述。遗传迭代计算出来的库位分配结果如图中粉色色块所示,1号汽车存放在66号库位,2号汽车存放在76号库位等。由图可知,取车优先时,车辆存放位置多集中在出口处,且VIP等级较高的6、11、12、18及19号车相对靠近车库出口。 表1 基本仿真数据设定 图5 库位分配情况 3)常规入库 常规入库即按照空余车库编号从小到大依次存入,如图5中棕色色块所示。 下面计算三种不同的存车策略将20辆车存入车库所用的存、取车时间,如表2所示。 表2 存取车各策略的遗传算法结果比较 采用存车优先模式,存车时间相对于常规入库减少了4.35%,相对于取车优先提高了14.272%。采用取车优先模式分配库位,取车时间相对于常规入库分配减少了14.431%,相对于存车优先模式减少了15.078%。因此采用本文设计的库位分配方法能够在特定情况下有效减少存、取车时间,以适应不同时段的需求。 本文使用遗传算法求解自动化立体车库库位分配问题,在考虑会员优先策略的同时,设计了一种通过调整权重来改变库位分配策略的方法,以适应立体车库不同时段的需求。在存在50个空余库位、20辆待入库车辆的的情况下,得出以下结论:相对于常规入库方法,本文所设计的方法在存车优先时能够减少4.35%的存车时间,在取车优先时能够减少14.431%的取车时间,并且相对于同批入库的其他车辆,会员级别高的用户车辆被安排在更靠近车库出口的库位,实现了缩短高级会员取车等待时间的目标。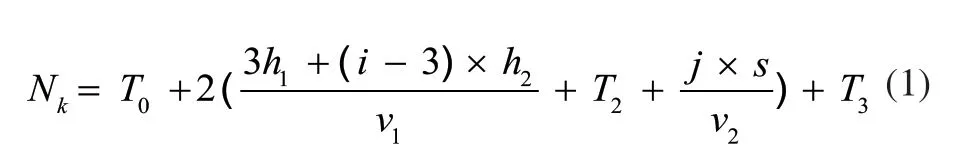


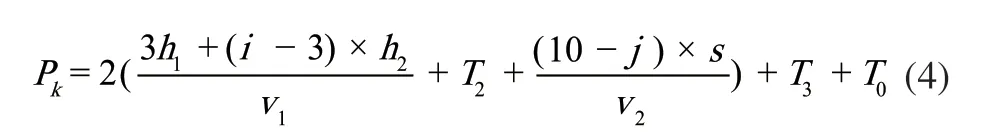



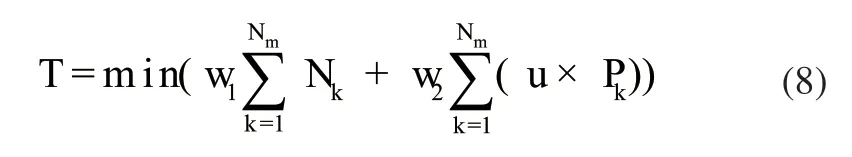
3.2 遗传算法求解
4 优化结果分析

5 结语
