浅析不定积分中的一题多解

王雅萍

(江苏商贸职业学院,江苏 南通 226001)

根据新课改的要求，在高职数学的教学过程中要注重对学生能力素养的培养，加强逻辑推理能力、抽象思维能力和创造创新力的培养，体验解决问题方法的多样性，提高学生的科学实践能力和探索创新精神。[1-2]

1 高职数学教学中存在的问题及解决策略

现实教学过程中，教师由于课时限制，为了紧扣教学任务，往往遵循先介绍概念公式，再讲解例题，最后练习巩固的学习程序，解题的方法通常只是教材上常见的一些常规解法。而学生在解答问题时只会单纯的模仿例题的解法，直接套用现成的公式，统一思路、统一方法、采用同样的格式，思维固化，对知识脉络理解不透彻，不能举一反三。

如果教学时注意“一题多解、一题多变、一题多问”，则可以打破学生思维的僵化，开拓新思路，对培养学生的发散思维能力，对知识融会贯通，从而锻炼思维的敏捷性，提高解决问题的灵活性，克服思维定式、思维僵化，形成丰富多彩的思维意识网，遇到问题可以灵活迅速地提出解决问题的各种方案。[3]

一题多解训练的方法有很多种，如纵横思维、变更命题发散、逆向思维、分解思维、构造思维等。通过一题多解，使学生能够思路开阔，探寻变异，多角度、多变化、多层次的将已知信息转换改造，扩散形成新的知识结构，这是一种开放性、立体性、灵活性、独创性的思维，是培养创新能力的核心。[4]练习不在多而在于精，将每道经典题目做深、做透，做广，这样才能全面、系统的整合知识脉络，理解各知识点之间的联系，使所学内容得到升华、深化，从而达到举一反三、触类旁通。

2 两类不定积分问题的解法分析

不定积分是高职数学中的教学重难点之一，这一节的题目千变万化，要学好这部分内容，学生一定要打好基础，掌握常用的一些积分基本公式以及求不定积分的常用方法：第一类换元积分法、第二类换元积分法、分部积分法等。接下来以不定积分中的“一题多解”为例，尽可能多地提出多种思路、寻求多种解答方法。[5]

方法1:第一换元法

这种方法通过分子分母同时乘以sinx，从而“无中生有”，凑出微分，达到换元的目的，这是一种常用的解题技巧。

方法2:

该方法2中利用三角函数的恒等公式将1变成了sin2x+cos2x，看似复杂了，却能很好的解决这类三角函数的积分问题。

方法3:

方法4:

方法3与4做法比较类似，分子分母同时乘以一个新的函数，这种看似“化简为繁”的做法往往可以很好地解决一些难题。

方法5:

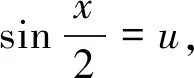
这里涉及到有理函数的积分，采用待定系数法得

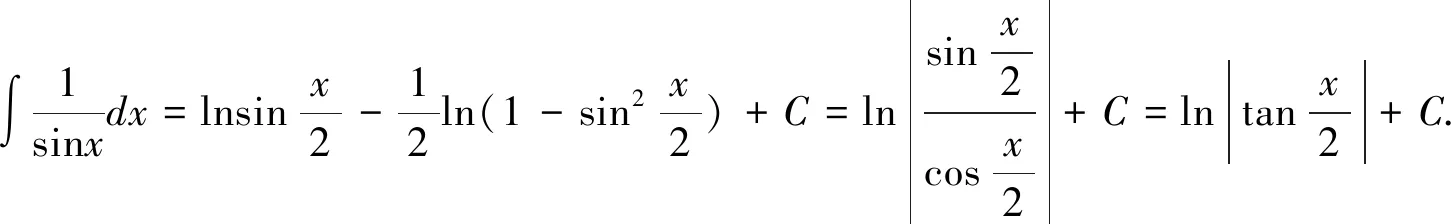
方法5用到了三角函数的半角公式，换元后，用到了有理函数的待定系数积分法，对学生拓宽结题思路有很好的帮助。

方法6:

方法6做法显然比方法5更简练清晰。

方法7:万能代换

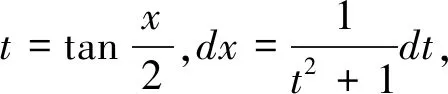
万能代换也是一种常用的解法。

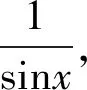
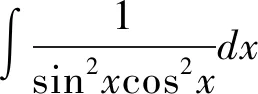
方法1：第一换元法

这种换元法是解决此类问题时比较常用的一种方法。

下面我们考虑利用第二类换元积分法。

方法3：无理代换[7]

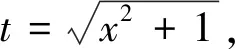
无理代换是除去被积函数中的根号的常见做法，这样可以降低积分难度。

方法4：三角代换(割代换)

令x=tant,dx=sec2tdt

方法4中的三角代换也是除去被积函数中根式的一种做法。

方法5：双曲代换

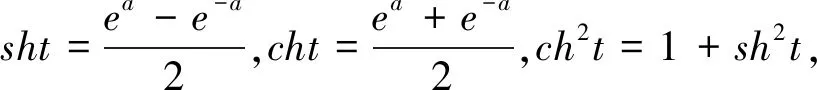
双曲代换是去除根式的好办法，在有些问题中比三角代换计算更简练。

方法6：欧拉第一代换

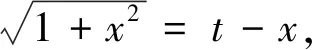
欧拉第一代换的解题做法换元过程相对复杂一点。

方法7:欧拉第二代换

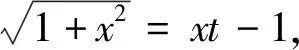
方法8：待定系数法

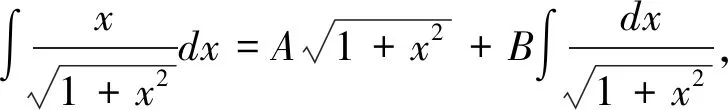
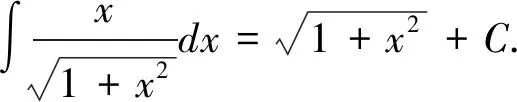
3 结 论

通过以上两类问题的求解过程，可以看到不定积分的解题技巧有很多种，不同的解题思路，表面上看是相互独立的，实际上知识点之间有着千丝万缕的联系.高等数学中还有很多题目可以发散思维、一题多解，我们应当打破解题思维的局限，精选例题，创设问题情境，鼓励学生以乐于求异作为一种重要的内驱力，注重观察积累，锻炼学生丰富、灵活、敏捷的思维方式，形成生动的多样性的意识网，迅速、从而提高学生的创新意识和创造能力。