一种混合装配线产品排序问题的研究
2019-12-04张世哲

Research on a Mixed-model Assembly Line Sequencing Problem
ZHANG Shi-zhe
摘要:针对带交货期时间窗的混合装配线产品排序问题进行研究。根据带交货期时间窗的混合装配线产品排序问题的特点建立混合装配线产品排序以提前/超期成本最小为目标的数学模型,并设计一种改进遗传算法进行求解。最后以一个案例为例,证明算法的有效性。
Abstract: In this paper, the mixed-model assembly line sequencing problem with delivery time window is studied. According to the characteristics of mixed-model assembly line sequencing problem with delivery time window, a mathematic model was established aiming at minimizing the cost of earliness/tardiness for the mixed-model assembly line sequencing problem. An improved genetic algorithm was proposed according to the model. Finally, the robustness of proposed algorithm was demonstrated by the benchmark instance.
关键词:排序问题;混合装配线;提前/拖期;遗传算法
Key words: sequencing problem;mixed-model assembly line;earliness/tardiness;genetic algorithm
中图分类号:TH162 文献标识码:A 文章编号:1006-4311(2019)32-0269-04
0 引言
随着社会的发展,混合装配线被越来越多的应用于实际生产中。而产品排序问题就成为了混合装配线优化过程中必须面对的问题。在某些高价值产品的生产过程中,经常会遇到以最小化产品提前/超期成本为目标的生产排序问题,这类产品往往具有价值较高、每件产品拥有其独立的交货期时间窗、不适合长期储存、延期交付将产生大量的延期交付成本等特点。工程机械就是这类产品的典型代表。
本文将针对混合装配线排序问题进行研究,建立数学模型,并设计一种改进遗传算法,以最小化产品排序的总提前/超期成本,从而提升企业效益。
1 产品排序问题的数学模型
1.1 带交货期时间窗的混合装配线产品排序问题
产品排序问题是一个典型的NP-hard问题。首先,对于混合装配线中产品的装配而言,多种相似产品在一条装配线上进行装配,每种产品由装配线起始工作站进入装配线开始装配,依次经过每个工作站,直至装配完毕,而每个工作站每种产品的装配时间并不相同。
其次,对于产品的交付而言,每种产品具有独立的交货期。若产品在最早交货时间之前完工,将产生库存成本、维护成本等提前交付成本。同样,若产品在最晚交货时间之后完工,将产生违约成本等超期成本。
带时间窗交货期的混合装配线排序问题就是通过合理安排产品进入装配线进行装配的顺序,使各产品的装配完成时间尽可能落在其交货期时间窗之内,以最小化总提前/超期成本的问题。不合理的生产排序将会导致较高的成本,严重影响企业效益。因此,通过合理安排各产品的装配顺序以使产品总提前/超期成本最小,对企业而言至关重要。
1.2 建立数学模型
首先,本文在建立相应的数学模型之前,作出如下假设:①每个产品不能同时在几个工作站进行装配,在某一时刻只能在一个工作站進行装配。②每个产品的装配一旦开始不能停止,中途不能插入其他产品进行装配。③产品依次通过各个工作站完成装配。④每种产品在各工作站的装配时间固定,与装配顺序无关。
为描述混合装配线排序问题,定义以下参数及变量:
[d,d]为第i类型第j个产品的交货期时间窗,d为第i类型第j个产品的最早交货时间,d为第i类型第j个产品的最晚交货时间;
D为计划期内所需生产产品总量;
N={1,…,n,…,D}生产产品集合;
np产品类型数量;
L={1,…,l,…,np}产品类型集合;
Ni为第i种产品的总生产量;
Tij为第i类型的第j个产品的完工时间;
ADi为第i类型产品的单位提前成本;
DEi为第i类型产品的单位延期成本;
Zij=01,若Zij=1,则第i个装配的产品为j类型产品;
最终得到混合装配线排序问题的数学模型为:
objective
公式(1)表示所有产品总提前/超期成本最小,其中max(d-Tij,0)表示第i类型的第j个产品的提前完工时间,ADimax(d-Tij,0)表示第i类型的第j个产品的提前成本,max(Tij-d,0)表示第i类型的第j个产品的延迟交付时间,DEimax(Tij-d,0)表示第i类型的第j个产品的超期成本。公式(2)表示每种产品产量必须与计划期内该品种产品需求量一致。公式(3)生产序列每个位置有且只能有1个产品。公式(4)表示变量Z的取值范围。
2 改进遗传算法
2.1 编码
产品排序问题由于只需要优化产品的装配顺序,因此,在利用遗传算法求解时,采用数字串编码的方式进行编码。每条染色体表示一个可行产品装配顺序,染色体上每一个基因表示一个产品,染色体的长度即为该生产周期内所需生产产品的总量。染色体生成的步骤为:①确定所需生产产品类型数量以及各类型产品数量。②在当前可生产产品类型中随机选择一种产品放入染色体对应位置。③所选类型产品生产数量减1,更新所需生产产品类型以及各类型产品所需生产量。④若更新后所需生产产品类型数量不为0,则返回步骤2,若更新后计划期内所需生产产品类型数量为0,则结束。
按照同样方法進行重复,即可形成种群。
2.2 适应度计算
首先,对每一个染色体计算其所对应的提前/超期成本。由于本文所解决排序问题目标为最小化问题,因此,需将每个染色体所对应的提前/超期成本进行一定的处理转化为适应度值,本文所采用的提前/超期成本与适应度的转化公式为:
式中fi为每个个体的适应度值,mi为每个个体的提前/超期成本。
2.3 稳态选择
本文选择稳态选择策略作为排序问题的选择方式,即选择少量个体进行之后的交叉、变异操作。每个个体被选中的概率计算公式为:
式中Pi为个体i被选中的概率,fi为个体i的适应度值,I为当前种群。
之后,根据每个个体被选中的概率选择少量个体组成交配池进行之后的交叉、变异操作。
2.4 交叉
染色体的交叉采用次序交叉的方式进行处理,以下举例说明:
假设,某条装配线生产7种类型产品,每种产品均只生产一个,经编码、选择后产生交配池,从当前交配池中,随机选取两条染色体,假设两条染色体如图1、图2所示。
随机选取染色体1中的两个交叉点,并将交叉点间的基因删除,假设选取交叉点为3和6,如图3所示。
将染色体2中染色体1保留部分依次删除,如图4所示。
将染色体2中剩余部分依次插入染色体1中所删去部分得到子染色体1,如图5所示。
按照同样交叉方式对染色体2进行处理将得到子染色体2。
2.5 变异
在进行完交叉操作后,需进行变异操作,本文对染色体的变异设定一个变异方向。首先,从交叉产生的子代群体中,随机选取一个染色体。之后,随机选择该染色体的一个基因,根据所选取基因的提前/超期成本进行调整,若该基因产生了提前入库成本,则将该基因向染色体尾部方向调整,若该基因产生了超期成本,则将该基因向染色体头部方向调整。以下举例说明,仍然采用上文中案例进行说明。
首先从交叉后生成的子代中,随机选择一条染色体,假设上文案例中所生成的子代中随机选择一条染色体如图6所示。
随机选择一个基因,假设选择基因4。若该基因存在超期成本,则将该基因随机插入其左侧染色体部分,如图7所示。
若该基因存在提前入库成本,则将该基因随机插入其右侧染色体部分,如图8所示。
在完成变异操作后,将生成的子代个体代替原种群中最差的等量个体遗传至下一代中。
2.6 局部寻优
为使算法更快速收敛到最小值附近,本文在遗传算法完成遗传操作后,对种群中个体进行局部寻优。本文在对种群个体进行局部寻优时,仅对种群中少量较优个体进行局部寻优。
在对个体进行局部寻优时,借鉴邻域搜索以及2-OPT算法的思想进行处理。本节仍以上文中案例为例进行说明,假设经过上文的遗传变异后,形成新种群,从新种群中选择少量最优个体进行局部寻优,假设某进行局部寻优操作染色体如图9所示。
利用2-OPT算法的思想构建一个所选染色体的邻域染色体,即对当前染色体随机选取两个基因,并将两个基因之间的基因进行倒序排列,假设选取位置为2和6,之后对两个基因之间的染色体部分进行倒序,所得到的新染色体即为一个邻域染色体。如图10所示。
在得到一个新的邻域染色体后,判断新染色体是否优于原染色体,若优于原染色体,则用该染色体代替掉原染色体,并对该新染色体进行邻域搜索,直至达到结束条件退出局部寻优,若不优于原染色体,则继续对原染色体进行搜索,直至达到结束条件退出局部寻优。
3 算例分析
3.1 算例
某工程机械制造公司共需生产10种产品共120台机械,10种产品均在一条混合装配线上进行生产,每种产品的生产数量如表1所示。
在装配过程中,各产品依次经过12个工作站进行装配,每种产品在各工作站的装配时间如表2所示。
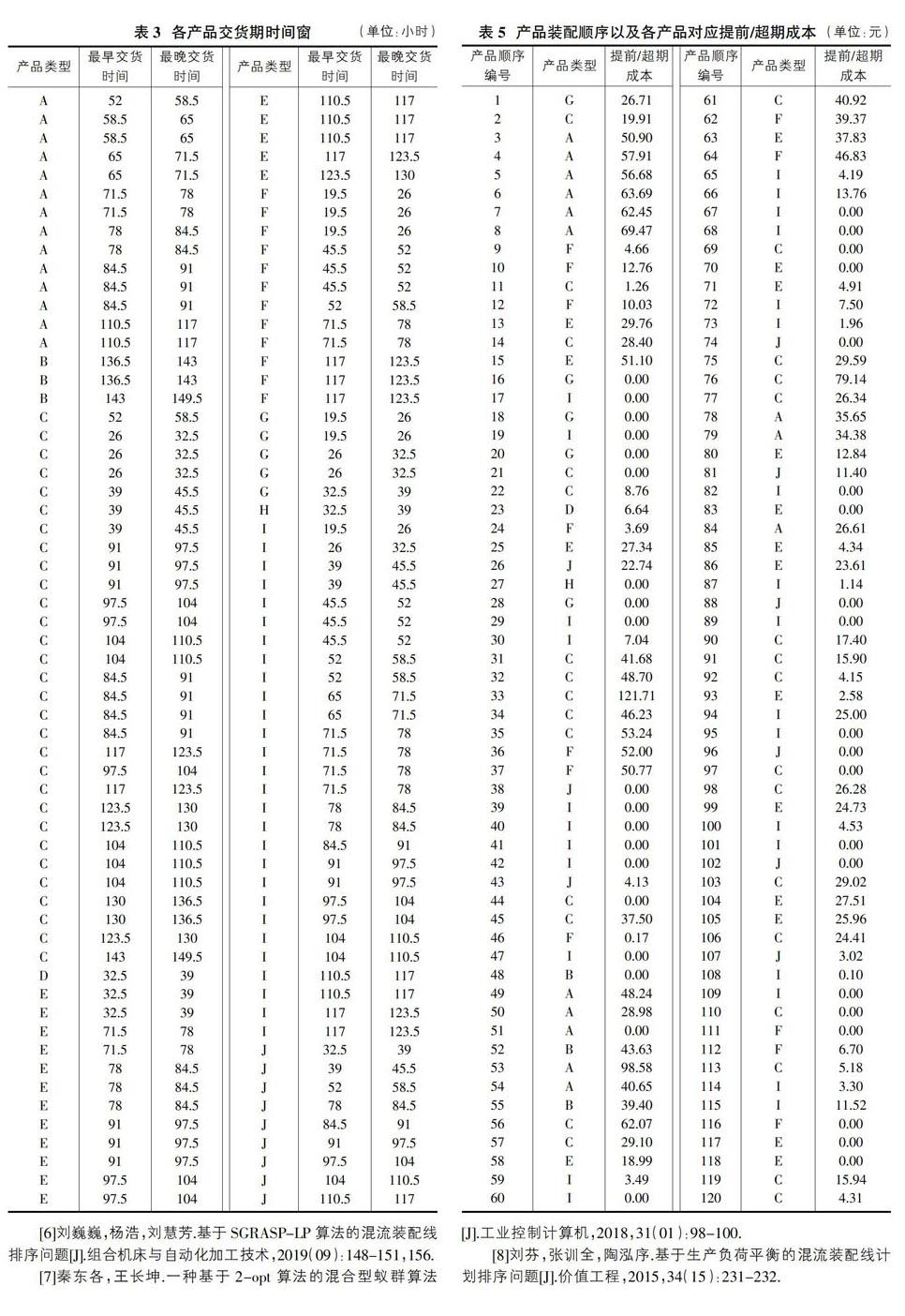
将第一个产品进入装配线装配的时间设置为0时刻,各产品的所对应的交货期时间窗如表3所示。
每种产品的提前超期成本如表4所示。
3.2 结果分析
将案例数据数据带入算法进行优化,算法相关参数设置如下:种群数量100、交叉概率0.9、变异概率0.01、稳态选择数量20、迭代次数100、对每代中最优的20个个体进行局部寻优,寻优代数为100。
将数据带入算法,经过优化后,得到最优产品生产序列,所有产品均未产生超期成本,每种产品的提前/超期成本、生产顺序如表5所示。
经计算,总提前/超期成本为2251.02元。
3.3 稳态选择策略与其他遗传算法的比较
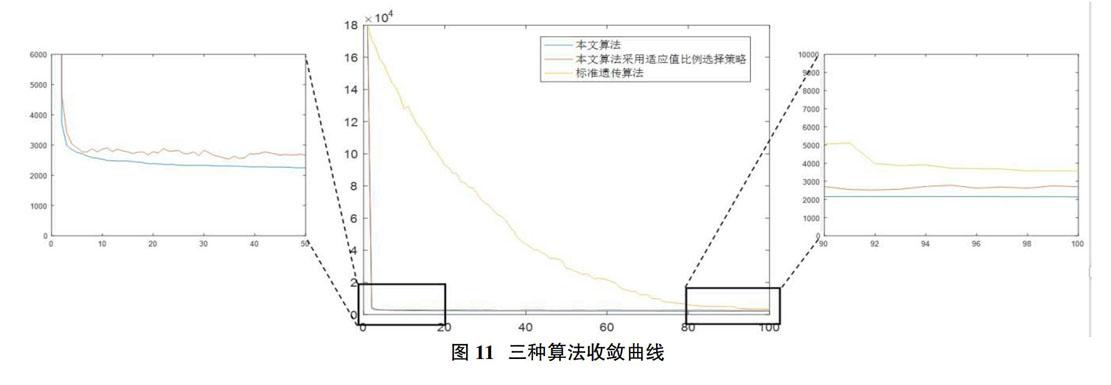
将本文算法与标准遗传算法以及将本文算法中选择策略替换为适应值比例选择策略的算法进行比较,三种算法的目标值收敛曲线如图11所示。
由图中信息可发现,本文算法在收敛速度上明显优于标准遗传算法,略优于本文算法选择策略采用适应值比例选择策略算法。在结果上,本文算法明显优于另外两种算法。
4 结论
本文针对以最小化产品总提前/超期成本最小为目标的混合装配线排序问题进行研究,建立了相应的数学模型,并设计了一种基于稳态选择策略的改进遗传算法,通过与传统遗传算法以及其他几种遗传算法选择策略进行对比,证明了稳态选择策略的优越性。为企业解决实际产品排序问题提供了方法。
参考文献:
[1]李逍波,林争辉.一种高效稳态型遗传算法结构[J].上海交通大学学报,1998(01):7-9.
[2]郑姣,杨侃,郝永怀,周冉,刘国帅.基于稳态繁殖的遗传算法在水库优化调度中的应用[J].水电能源科学,2011,29(08):38-41.
[3]范丽,张育林.基于稳态遗传算法的间歇式覆盖天基雷达星座优化设计[J].国防科技大学学报,2006(02):17-21.
[4]张贵军,吴惕华,叶蓉.CTSP问题稳态小生境算法的研究及仿真实现[J].系统仿真学报,2004(08):1692-1696.
[5]宋华明,马士华.考虑流水线平衡的混合装配线排序[J].中国机械工程,2006(11):1138-1141,1147.
[6]刘巍巍,杨浩,刘慧芳.基于SGRASP-LP算法的混流装配线排序问题[J].组合机床与自动化加工技术,2019(09):148-151,156.
[7]秦东各,王长坤.一种基于2-opt算法的混合型蚁群算法[J].工业控制计算机,2018,31(01):98-100.
[8]刘芬,张训全,陶泓序.基于生产负荷平衡的混流装配线计划排序问题[J].价值工程,2015,34(15):231-232.
作者简介:张世哲(1995-),男,山西长治人,硕士研究生,研究方向为运营管理。
