筒体结构剪力滞后效应分析

胡启平 沈飞扬

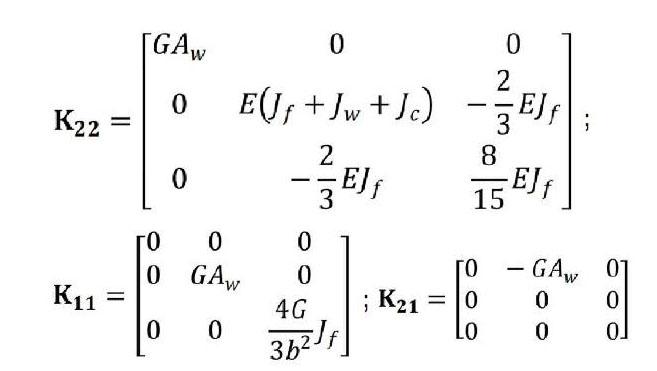
Analysis of Shear Lag Effect of Tube Structure

HU Qi-ping SHEN Fei-yang

摘要：本文探讨了筒体结构在水平集中力的作用下，在翼缘框架中所引起的剪力滞后效应的问题。首先，本文根据连续化原理，将密柱深梁的框筒等效连续化为由正交各向异性板和角柱围成的等效实腹筒，建立筒体结构的等效连续化力学模型;然后根据基本假定导出筒体结构在受弯时的哈密顿对偶体系，假定翼缘框架翘曲位移沿板宽方向呈二次曲线分布，而不考虑腹板的剪力滞后效应，其位移曲线为直线;其次，编制有效的MATLAB程序，应用精细积分法计算结构受弯时的数值解;最后，结合材料力学公式，求出结构的各项内力与位移，并证明本文方法的可行性。

Abstract： In this paper， the shear lag effect caused by the horizontal concentrated force in the flange frame of a cylindrical structure is discussed. First， according to the principle of continuum， the equivalent cylinder continuum mechanics model of the thick cylindrical column is equivalent continuous into the equivalent solid belly tube surrounded by orthotropic plates and corner columns. The equivalent continuum mechanics model of the cylinder structure is established. Then， according to the basic assumption， the duality system of the cylinder structure in bending is derived. It is assumed that the warpage displacement of the flange frame has a two degree curve distribution along the slab width， and not that of the cylinder. Considering the shear lag effect of web， its displacement curve is straight line; secondly， an effective MATLAB program is compiled to calculate the numerical solution of the structure under bending by the precise integration method; finally， the internal forces and displacements of the structure are obtained by combining the material mechanics formula， and the feasibility of this method is proved.

關键词：筒体结构;剪力滞后;哈密顿对偶体系;精细积分

Key words： tube structure;shear-effect;Hamilton duality solution system;precise integration

中图分类号：TU973.17                                  文献标识码：A                                  文章编号：1006-4311（2019）32-0219-02

0  引言

筒体结构因自身的整体性而具备良好的抗侧力性能，这使得其在实际工程中得到了广泛的应用，也成就了筒体结构在学术研究中的价值与地位。筒体结构的计算方法有很多种，例如空间杆系有限元矩阵位移法、等效连续体法、简化为平面结构法[6]等等;本文着重于筒体结构的剪滞效应，采用精细积分法[5]，计算结构的内力与位移。

1  筒体弯曲问题的计算模型和基本假定

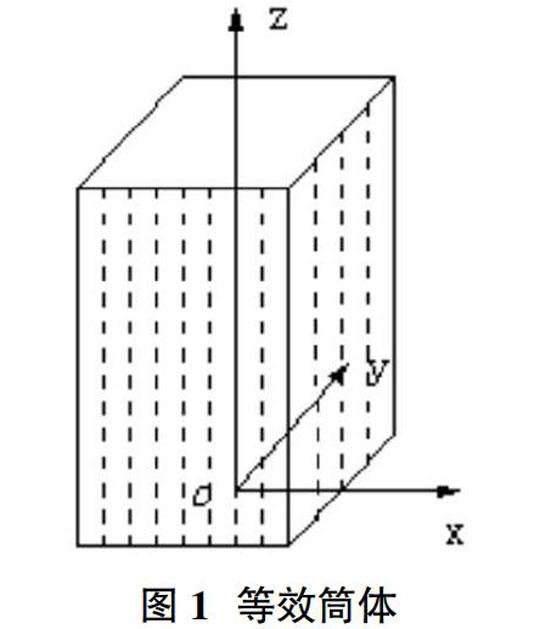
本文采用连续化假定[1]，将筒体等效连续化为正交异性实腹薄壁筒。t为等效板厚度，E为材料的弹性模量，G为材料的剪切模量。选用笛卡尔坐标系，O为截面形心，Ox、Oy为截面形心主惯性轴，z为筒体轴线，如图1所示。

把等效筒自底向顶用结线划分为n个等宽窄条，宽度为d，窄条的竖向边界为结线，各窄条通过结线连接在一起构成筒体结构。选取三个广义位移：侧移u（z）、截面转角θ（z）及最大位移差函数W（z），当假定翼缘框架翘曲位移沿板宽为二次曲线分布，腹板框架为直线时[2]，此时翼缘与腹板的位移有如下表示：

翼缘位移：

腹板位移：

角柱位移：

式（1）中第一项是初等梁理论的结果，第二项为考虑了剪力滞后修正后的结果，即摒弃了初等梁理论中的平截面假定;假定地基为刚性地基，基础顶面的侧移、转角和纵向位移都为零，且楼板为刚性，即只考虑壁板的平面内作用。

2  筒体弯曲问题的哈密顿对偶求解体系

翼缘应变能：

腹板应变能：

角柱应变能：

外力势能（若结构受沿高度变化的分布荷载q作用）：

式（1）、（2）、（3）已经给出了翼缘、腹板和角柱的翘曲位移函数，将它们分别代入式（4）、（5）、（6），能够得到翼缘、腹板和角柱的应变能：

翼缘应变能：

腹板应变能：

角柱应变能：

结构总应变能：

故可得总势能密度即拉格朗日函数为：

拉格朗日函数标准表达式为：

当有了K22、K11和K21，即可按照基于两端边值问题的精细积分法，编制有效的MATLAB程序对结构的内力和变形进行计算。

3  算例

如图2所示为一筒体结构平面图[4]，平面尺寸为30m×36m，层高3.0m，共20层;角柱截面0.9m×0.9m，中柱截面0.5m×0.9m，柱距3m，梁截面0.35m×0.8m，荷载为顶部的集中力P=2000kN。钢筋混凝土弹性模量E=3×104MPa。

4  结论

通过算例对比能够看出，本文计算结果与文献方法结果有着较高的相似度，其存在的誤差处于允许范围，可证明本文应用的基于两端边值问题的精细积分法，对考虑剪力滞后时筒体结构的计算是可行且有效的。

参考文献：

[1]胡启平，王妨.框筒结构剪力滞后分析[J].硅谷，2010（08）：78-79.

[2]周娟.筒体结构弯扭分析的精细积分法[D].河北工程大学，2008.

[3]包世华.高层建筑结构计算[M].北京：高等教育出版社，1990.

[4]包世华，张铜生.高层建筑结构设计和计算[M].北京：高等教育出版社，2013.

[5]胡启平，孙良鑫，高洪俊.铁摩辛柯梁弯曲问题精细积分法[J].工业建筑，2007（S1）：268-270.

[6]金仁和，魏德敏.框筒结构剪力滞后研究现状与思考[J].建筑钢结构进展，2008（02）：23-27.

作者简介：胡启平（1963-），男，安徽霍邱人，硕士，教授，研究方向为力学;沈飞扬（1994-），男，河北邢台人，硕士，研究方向为建筑与土木。