一种基于APSK的矩形差分空间调制算法

罗昀 邹嵘

Amplitude Phase Shift Keying Aided Rectangular Differential Spatial Modulation

LUO Yun ZOU Rong

摘要：本文提出了一种用于多输入多输出（MIMO）系统的结合幅度相移键控（ASPK）的新型差分空间调制方法。该方法结合APSK与RDSM调制，在保留了RDSM矩形天线索引矩阵的结构下，利用APSK调制来进一步提升了频谱效率。通过仿真结果比较了所提算法相比于传统差分空间调制的性能差异。

Abstract： In this paper， a novel amplitude phase shift keying Aided rectangular differential spatial modulation （APSK-RDSM） is proposed for multiple-input and multiple-out （MIMO） system， which combines the amplitude phase shift keying （APSK） and rectangular differential spatial modulation （RDSM） to take the advantages of RDSM and STBC systems， while avoiding the drawbacks of conventional differential spatial modulation （DSM） systems. Finally， simulation results demonstrate that APSK-RDSM outperforms the conventional DSM systems for various spectral efficiencies.

关键词：差分空间调制（DSM）;幅度相移键控（APSK）;MIMO

Key words： differential spatial modulation （DSM）;amplitude phase shift keying （APSK）;MIMO

中图分类号：TN914                                      文献标识码：A                                  文章编号：1006-4311（2019）32-0191-04

0  引言

差分空间调制技术（Differential Spatial Modulation，DSM）[4]-[7]是一种基于空间调制技术，在接收端采用非相干检测的新型MIMO技术。发射端采用激活的传输天线矩阵索引和星座符号传输信息，通过在发射端进行差分编码从而在接收端可以在没有信道信息的情况下准确恢复出发送的信息。

文献[13]提出了一种矩形差空间调制方案，信息通过一个矩形向量而不是传统的方形矩阵发射，大大减少了天线传输矩阵数量。为了进一步提高差分空间调制系统的频谱效率，我们考虑将APSK[14]调制应用到RDSM系统了，并设计该方案的差分映射方案，利用APSK调制来进一步提升传输速率和性能。

1  RDSM系统

在RDSM系统中，比特信息通过天线索引矩阵和调制符号共同传输。传统差分空间调制中，当前个时隙的调制符号向量与前个时隙的传输符号向量做差分编码后再进行传输，而在RDSM系统中，只需当前时隙的调制符号向量与上一个時隙的传输符号向量做差分编码。RDSM系统大大减小天线索引的数量，在大规模MIMO系统中仍然适用。

2  结合APSK调制的RDSM

本节提出一种结合APSK调制的RDSM系统。该方法结合APSK与RDSM调制，在保留了RDSM矩形天线索引矩阵结构的下，利用APSK调制来进一步提升了频谱效率。具体来说，比特信息通过天线索引，调制符号和PSK幅度共同传输，同时调制符号和PSK幅度映射到矩形天线索引矩阵与上一时刻传输矩阵进行差分编码。

2.1 APSK-RDSM系统模型

系统框图如图1所示。考虑一个发射天线数为Nt，接收天线数为Nr的MIMO系统，长度为B的发射信息比特分为B1、B2和B3三个部分。B1=log2（Q）个比特用来选择传输天线向量ak（q=1，…，Q），其中ak是一个Nt×1维向量，且只有一个元素为1，其他元素均为0;B2=1og2（L）比特用来调制M-PSK星座符号（s1，s2…，sM），M表示PSK调制星座图大小。B3=1个比特用来选择PSK调制幅度。PSK的幅度从rH和rL中二选一，rH和rL满足：

则每个时隙传输的比特为■。

第k个时隙的符号向量可以表示为：

通过差分编码得到第k个时隙的发射向量sk∈CM如下：

最后再对差分后得到的发射向量进行APSK调制。加入APSK幅度信息后得到第k个时隙的发射向量

其中

b表示第i个时隙传输比特中用于PSK幅度调制的B3个比特。即若b=[0]，则λk=1，ηk=ηk-1，当前时隙与上一个时隙的PSK符号幅度相同;若b=[1]，则λk当前时隙与上一个时隙的PSK符号幅度相反，即上一个时隙PSK符号幅度若为rL，则，当前时隙PSK符号幅度为rH;上一个时隙PSK符号幅度若为rH，则，当前时隙PSK符号幅度为rL。

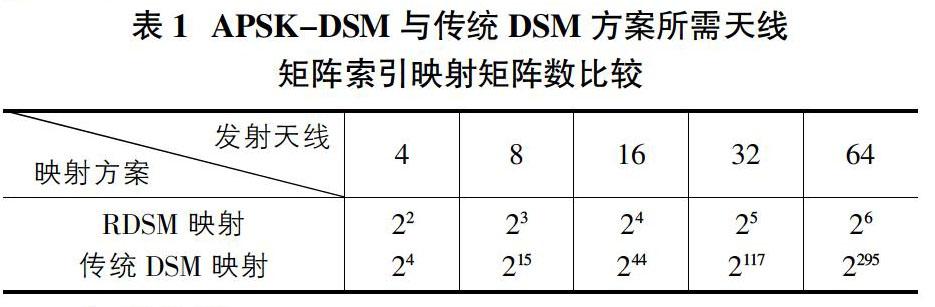
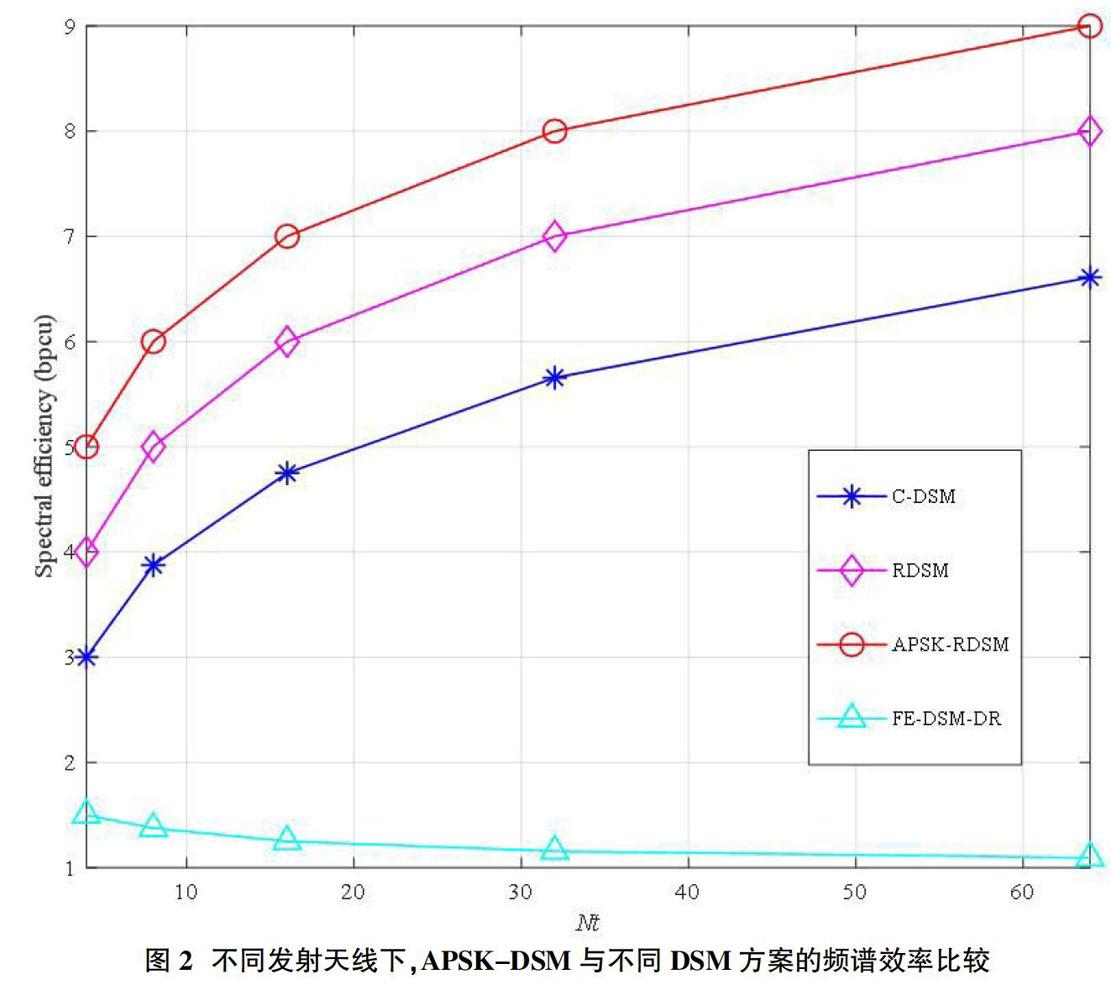
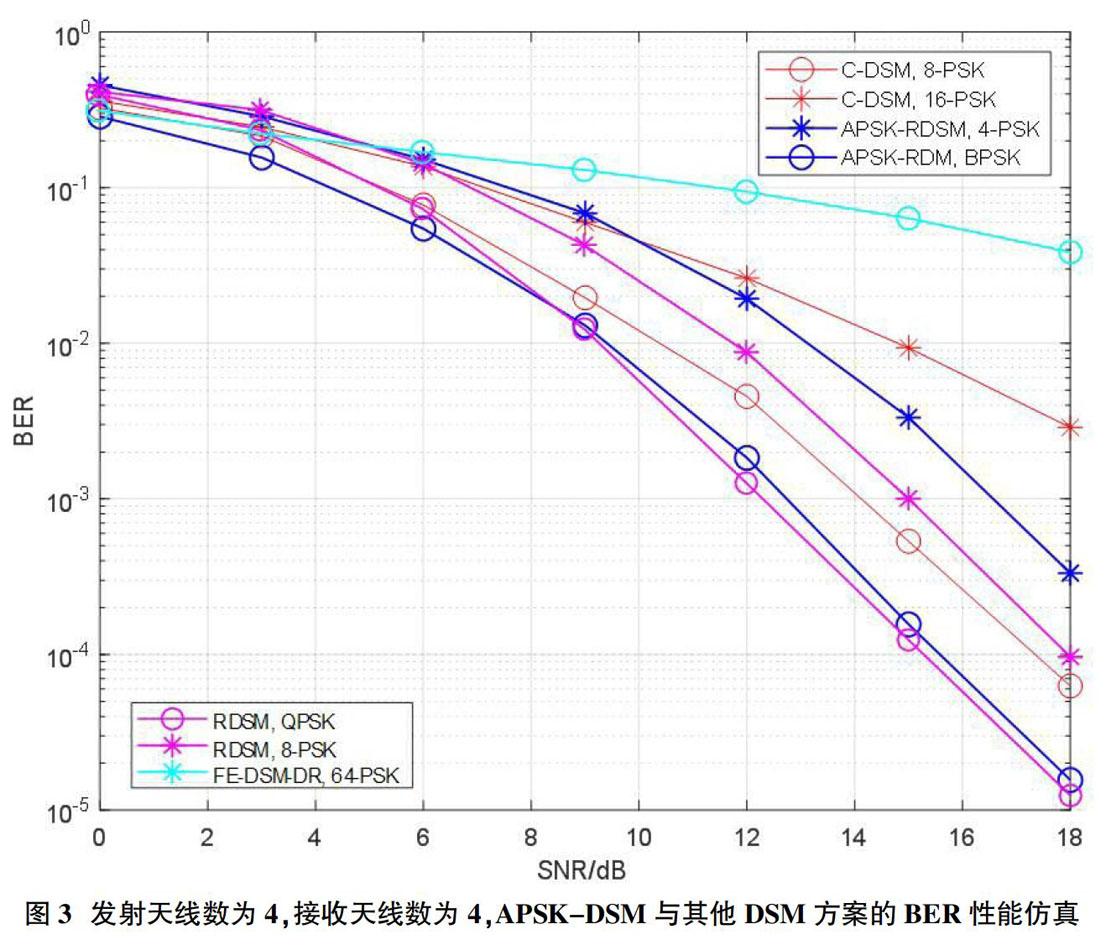
前Nt個时隙发送的参考符号，对于第k

以Nt=4，BPSK调制为例，则每个时隙传输的比特为比特。

假设第k（k>Nt）个时隙传输的比特为传输比特分为和B3=1三部分。前B1=2个比特用来选择选择传输天线向量后B2=1个比特（0）经BPSK调制为+1，即sk=+1。则假设第k-1个时隙的发射向量为

则k个时的发射向量

第k个时隙用于APSK调制的比特b=[1]，则与上一个时隙的PSK符号幅度相反，由于第k-1个时隙的PSK幅度为rH，可以得到最终的发射向量为。

2.2 检测算法

令表示没有加入APSK幅度所有可能的差分调制符号向量集合，表示APSK调制幅度集合，则发射符号向量结合可以表示为，可以得到APSK-RDSM的检测算法为：

其中，

其中。由于包含前（i-1）个估计符号和前（i-1）个接收符号，该检测方法受错误传播影响较大。引入参数α用来减小错误传播。对于，α取值为0，且;对于i>Nt，α的最优值可以通过最小化来得到。本文中仿真α的取值为0.9。

3  仿真结果

本节比较所提APSK-RDSM方案与其他DSM方案的频谱效率，并给出在不同参数下APSK-RDSM系统与其他DSM方案的BER性能仿真对比。所有的仿真结果都通过蒙特卡洛仿真来评估，且所有每个符号间隔的发射能量都进行了归一化处理。

图2比较了采用QPSK调制时，APSK-RDSM与其他DSM方案随天线数增加的频谱效率。从仿真结果可以看到，在这两种情况下，APSK-RDSM的性能都要优于传统差分空间调制。

图3比较了发射天线数为4，接收天线为4时APSK-RDSM与C-DSM的BER性能。其中，C-DSM表示传统差分空间调制[4]，RDSM表示矩形差分空间调制[12]，FE-DSM-DR表示改进的基于代数域拓展的差分空间调制[13]。从图上可以看到，在相同的天线配置和调制方式下，APSK-DSM的频谱效率要高于其他差分调制方案。从表1可以看到，RDSM映射大大减少了索引比特映射所需映射矩阵数，同时得到了比传统DSM映射更高的传输比特数。特别的，当发射天线数增大时，传统DSM方案由于所需天线矩阵索引映射矩阵数急剧增加而几乎无法用于实际通信中。同时，APSK-DSM方案由于同时对PSK调制幅度进行了差分映射，APSK-DSM可以获得比RDSM更高的传输速率。

4  结束语

本文提出了一种结合APSK的新型差分空间调制方案。在所提算法中，比特信息通过矩形差分矩阵和PSK幅度传输，在减小了发射天线矩阵的数量的同时，利用APSK来进一步提升了频谱效率。避免了传统差分系统随着天线增加，发射天线矩阵急剧增加缺点。最后，通过仿真结果验证了所提算法在相同频谱效率下，相比于传统的差分空间调制能获得一定的性能增益。

参考文献：

[1]R. Mesleh， H. Haas， S. Sinanovic， C. W. Ahn， and S. Yun， Spatial modulation， ＼emph{IEEE Trans. Veh. Technol.}， vol. 57， no. 4， pp. 2228-2241， Jul. 2008.

[2]M. Di Renzo， H. Haas， and P. M. Grant， Spatial modulation for multiple-antenna wireless systems： A survey， ＼emph{IEEE Commun. Mag.}， vol. 49， no. 12， pp. 182-191， Dec. 2011.

[3]R. Mesleh， H. Haas， C. W. Ahn， and S. Yun， Spatial modulation-a new low complexity spectral efficiency enhancing technique， in ＼emph{Proc. Conf. Commun. Netw. China}， Beijing， China， pp. 1-5， Oct. 2006.

[4]Y. Bian， M. Wen， X. Cheng， H. V. Poor， and B. Jiao， A differential scheme for spatial modulation， in ＼emph{ Proc. 2013 IEEE Globecome. Conf.}， Atlanta， USA， pp. 3925-3930， Dec. 2013.

[5]M. Wen， Z. Ding， X. Cheng， Y. Bian， H. V. Poor， and B. Jiao， "Performance analysis of differential spatial modulation with two transmit antennas，" ＼emph{IEEE Commun. Lett.}， vol. 18， no. 3， pp. 475-478， Mar. 2014.

[6]L. Xiao， P. Yang， X. Lei， Y. Xiao， S. Fan， S. Li， and W. Xiang， "A low-complexity detection scheme for differential spatial modulation，" ＼emph{IEEE Commun. Lett.}， vol. 19， no. 9， pp. 1516-1519， Sep. 2015

[7]S. Sugiura and L. Hanzo， Effects of channel estimation on spatial modulation， ＼emph{IEEE Signal Process. Lett.}， vol. 19， no. 12， pp. 805-808， Dec. 2012.

[8]Y. Bian et al.， Differential spatial modulation， ＼emph{IEEE Trans. Veh. Technol.}， vol. 64， no. 7， pp. 3262-3268， Jul. 2015.

[9]N. Ishikawa and S. Sugiura， Unified differential spatial modulation， ＼emph{IEEE Wireless Commun. Lett.}， vol. 3， no. 4， pp. 337-340， Feb. 2014.

[10]W. Zhang， Q. Yin， and H. Deng， Differential full diversity spatial modulation and its performance analysis with two transmit antennas， ＼emph{IEEE Wireless Commun. Lett.}， vol. 19， no. 4， pp. 677-680， Apr. 2015.

[11]R. Rajashekar， N. Ishikawa， S. Sugiura， K. V. S. Hari， and L. Hanzo， Full-diversity dispersion matrices from algebraic field extensions for differential spatial modulation， ＼emph{IEEE Trans. Veh. Technol.}， vol. 66， no. 1， pp. 385-394， Mar. 2016.

[12]R. Rajashekar， C. Xu， N. Ishikaw， S. Sugiura， K.V.S. Hari， and L. Hanzo， Algebraic differential spatial modulation is capable of approaching the performance of its coherent counterpart， ＼emph{IEEE Trans. Commun.}， vol. PP， no. 99， pp. 1-1， DOI 10.1109/TCOMM.2017.2720170， Jun. 2017.

[13]N. Ishikawa， and S. Sugiura， Rectangular differential spatial modulation for open-Loop noncoherent massive-MIMO downlink， ＼emph{IEEE Trans. Wireless Commun.}， vol. 16， no. 3， pp. 1908-1920， Mar. 2017.

[14]P. A. Martin， Differential spatial modulation for APSK in time-varying fading channels， ＼emph{IEEE Commun. Lett.}， vol. 19， no. 7， pp. 1261-1264， Jul. 2015.

作者簡介：罗昀（1978-），男，四川成都人，高级工程师，硕士，研究方向为数字信号处理;邹嵘（1986-），男，贵州罗甸人，工程师，硕士，研究方向为通信系统。