煤层气储层孔渗参数的应力响应特征

吴 双，汤达祯，李 松，李 翔

（1.中国石化石油勘探开发研究院，北京 100083；2.中国地质大学（北京）能源学院，北京 100083；3.中联煤层气国家工程研究中心有限责任公司，北京 100095）

孔隙度和渗透率是评价储层储集和渗流能力的关键物性参数，一定程度上决定着油气井的产能和开发效益。煤层气是一种自生自储于煤层中的非常规天然气资源。相比于常规油气储层，煤储层的孔渗值整体偏低，并且具有较强的应力敏感性［1-3］。原始条件下的煤储层被地层水所饱和，作用于煤岩体上的有效应力可近似表示为地应力与储层流体压力之差；在实际开发过程中，随着地层水持续排出，储层流体压力降低，导致有效应力增大，孔-裂隙进而闭合，孔隙度和渗透率呈指数型急剧减小［4-6］。物体在应力作用下产生的相对力学变形即为应变，可分为轴向应变、径向应变和体积应变。煤储层孔渗参数在应力条件下的改变，本质即为孔-裂隙受挤压发生形变，这与煤岩的力学应变密切相关［7-8］。前人已研究并建立了一系列考虑有效应力、基质收缩、滑脱效应等影响因素在内的孔渗数学模型［9-14］，但这类模型主要是用热力学变化取代煤基质收缩，所涉及的应变量是基于煤层气解吸引起的兰氏体积应变，并不是基于孔隙力学形变引起的体积应变，其推导思路多是煤层气解吸改变体积应变—改变应力—改变储层渗透率，且有效应力对孔渗的影响效应间接通过煤岩力学参数（如体积模量、单轴模量）体现，并未直接将应力与渗透率联系起来。结合前人研究成果，弱化其他影响因素，仅考虑有效应力对孔渗变化的作用机制，建立了基于单轴力学形变理论下的孔渗计算模型，推导思路为改变应力—改变体积应变—改变孔渗参数，并将实测力学实验数据代入模型，求得不同轴向应力下的孔隙度和渗透率。同时，通过将传统火柴束模型中的孔隙压缩系数常量替换为“平均孔隙压缩系数”函数，分析了动/静态孔隙压缩系数引起的孔渗差异变化，该研究认识对煤储层物性评估具有理论指导意义。

1 单轴力学实验样品及方法

2 块煤样分别采自彬长矿区亭南煤矿和晋城矿区郭庄煤矿，因煤级差异，孔渗性存在差异，用于实验平行对比。实验室加工成轴向垂直层理的标准岩心，无肉眼可见的大割理存在。先放入烘干箱在80 ℃条件下烘干，再放入干燥箱在常温条件下冷却。样品信息见表1。

表1 煤样基本信息Table1 Basic information of coal samples

煤岩的单轴加卸载实验在岩石力学实验仪上完成。加载模式设为位移控制，加载速度设为0.005 mm/s，应力先由0逐渐加载至3.0 MPa，再以相同速度由3.0 MPa 逐渐卸载至0，加卸载过程进行一次。将传感器置于圆柱体煤样的横截面和侧面，实验过程中通过传感器获取轴向及径向应变数据。

2 轴向应力下的孔渗变化特征

2.1 单轴力学实验结果

从理论上说，煤岩在外力下的变形破坏过程可分为4 个阶段（图1）:①压密阶段，内部原生裂隙趋于闭合，应力-应变曲线在初始阶段下凹。②弹性变形及微裂隙扩展阶段，煤岩不仅产生弹性变形，部分微裂隙表面还会摩擦滑动，开始不稳定扩展破裂，应力-应变曲线表现为直线型。③扩容膨胀阶段，煤岩体积迅速膨胀，并由弹性变形转为塑性变形，微裂隙大量出现并扩展，此时应力-应变曲线偏离直线段且跳跃变化较大。④宏观破裂阶段，由于破裂过程比较迅速和突然，难以捕获此时的曲线［7，15-16］。

图1 应力-应变理论曲线Fig.1 Stress-strain theoretical curve

实验结果显示（图2），煤样的轴向应变（即轴向减小率）曲线在初始应力段下凹，之后随轴向应力的增大，曲线接近直线（图2a），表现出压密和弹性变形2个阶段特征，出于保护样品需要，实验施加的应力并未达到煤岩破裂极限，故实验所得的应力-应变曲线相比于理论曲线并不完整。径向应变（即径向增加率）随轴向应力的增大而线性增加（图2b），反映了煤岩沿层理方向非均质性相对较弱的特点。该实验数据将作为下文理论研究的基础数据。此外，应力-应变的加载线和卸载线不完全重合，卸载线滞后于加载线。唐杰等指出:岩石是由矿物颗粒固结形成，颗粒接触面间会有一些粗糙结构；在应力加载过程中，颗粒中心距离将随着外部应力的加载而改变，2 个粗糙面相互接触；应力下降时，由于粗糙面间的黏滑运动，应变不会即刻松弛，应力的释放先要克服颗粒之间的附着力和摩擦力，然后才能使岩石从弹性变形恢复［17］。应用颗粒接触粘合和黏滑摩擦机制能够解释观察到的滞后现象。

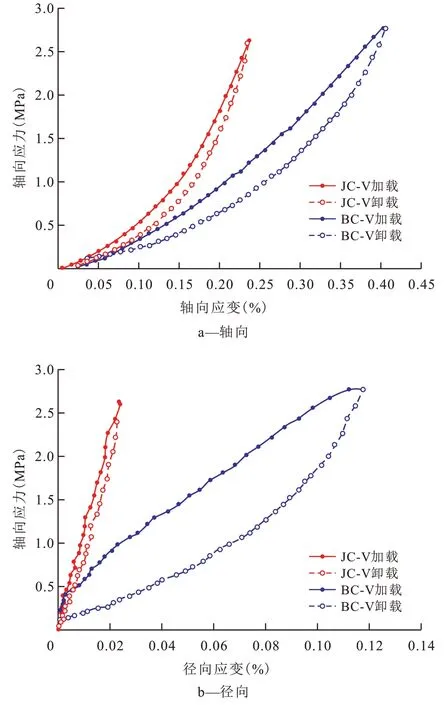
图2 实验煤样的应力-应变曲线Fig.2 Stress-strain curves of experimental coal samples

2.2 耦合力学应变的孔渗公式推导

当煤样不受围压（水平应力）约束时，仅在轴向压应力（垂直应力）作用下，轴向应变和径向应变同时产生（图3），其表达式分别为:

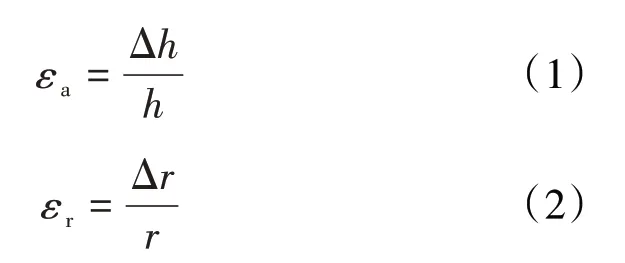
图3 煤样在轴向压应力下的变形示意Fig.3 Deformation diagram of coal sample under axial compressive stress

体积应变表示的是应力作用下，物体每单位初始体积下的体积变化量，可由轴向应变和径向应变相结合表示为:

联立（1）—（3）式，可得:

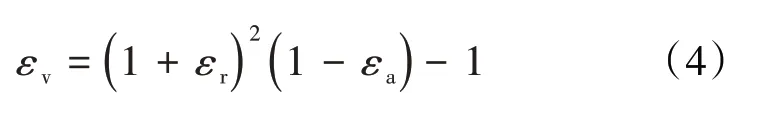
煤岩是由基质孔隙和割理裂隙构成的具有双重孔隙结构的多孔介质。在构建与应变相关的孔渗模型之前，假设其满足2个条件:①在低应力状态下，煤岩体积形变可近似认为是由煤岩体内孔-裂隙压缩引起。②毛细管迂曲度为一常数，不随煤岩变形而变化。基于假设条件，煤岩在应力作用下发生力学形变后的孔隙度可表示为:

由于在应力相对较低时，煤样总体积变化量约等于孔-裂隙体积变化量:

因此，耦合应变的孔隙度模型可表示为:

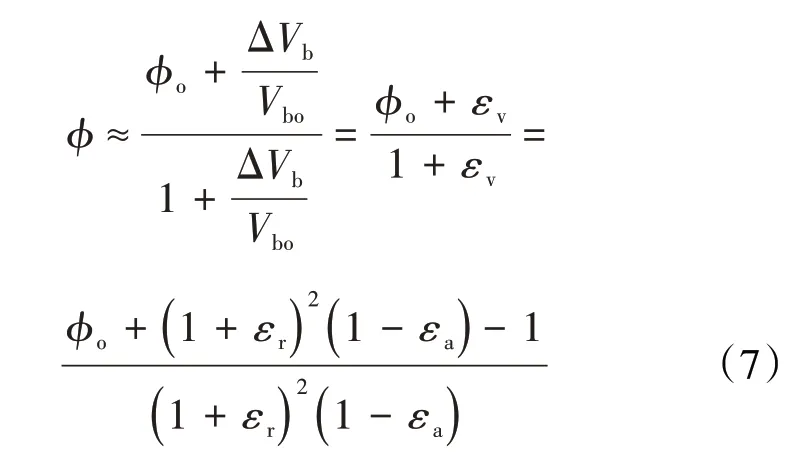
在假设的理想裂隙体系中，渗透率与孔隙度具有立方数量关系［18-19］，即:

联立（7）和（8）式，可求得耦合应变的渗透率模型，即:

根据（7）和（9）式，结合煤样力学测试数据，可求得对应各轴向应力的孔隙度和渗透率。随轴向应力增大，孔隙度和渗透率缓慢降低（图4），这与其他学者通过实验或现场测试得到的孔渗参数随应力变化趋势相一致［4，20］。由于施加在煤样上的轴向应力水平较低，因此孔隙度和渗透率下降幅度较小。相比于前人模型，基于形变理论的孔渗模型简化了参数配置，但当储层非均质性很强或应力增大到使煤储层发生塑性变形破裂时，该模型的应用受限。HEAP 等通过实验发现火山岩或结晶岩的孔隙度在循环载荷过程中不减反增，这便是由应力较大引起岩石塑性变形，大量微裂隙产生并扩展所致［21］。

3 孔隙压缩系数对孔渗变化的影响

3.1 孔隙压缩系数动态变化

孔隙压缩系数可用于定量评估孔-裂隙的可压缩性，将其定义为温度一定时，单位压差下的孔隙度变化量与初始孔隙度之比，即:

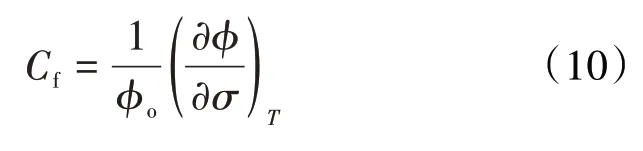
根据（10）式，结合煤样的孔隙度计算结果，可求得对应各轴向应力的孔隙压缩系数。随轴向应力的增大，孔隙压缩系数持续减小，在初始应力加载段的减小速率较快，随后逐渐放慢（图5）。这表明煤储层的孔隙压缩系数在变应力环境中不是常量，在低地应力背景下，孔隙压缩系数随地应力增大而快速减小；在高地应力背景下，孔隙压缩系数随地应力增大而缓慢减小。此外，孔隙压缩系数可以看作是储层致密化程度的体现，孔隙压缩系数大意味着可压缩空间大，储层致密化程度低，因此，在低地应力背景下，应力增大引起煤储层快速致密化；在高地应力背景下，应力增大引起煤储层致密化速度减慢，储层致密化程度趋于稳定。

图5 煤样孔隙压缩系数随应力变化趋势Fig.5 Variations of pore compressibility of coal samples with stress

煤岩是一种弹性地质体，具有极强的应力敏感性，倘若不考虑孔隙压缩系数受应力影响的动态变化，相关孔渗预测结果将失真。在一段应力区间的“平均孔隙压缩系数”可表示为［18］:

根据MCKEE 等［22］和SEIDLE 等［23］建立的火柴束模型，孔隙度和渗透率可表示为有效应力的负指数函数，即:

将（11）式代入（12）和（13）式，可得到变孔隙压缩系数下孔隙度和渗透率关于有效应力的改进火柴束模型，即:

作用于煤储层的有效应力通常可简化为上覆地应力与孔隙流体压力之差。由于实验中煤样经过干燥处理，不考虑孔隙流体压力，因此轴向应力可视为有效应力，（11）—（15）式中的有效应力变化量即为轴向应力变化量。基于这一前提，用（11）式拟合应力加载过程中的孔隙压缩系数变化趋势（图5），显示拟合度较高（图6），表明“平均孔隙压缩系数”函数（（11）式）适用于表征变应力下的孔隙压缩系数变化。

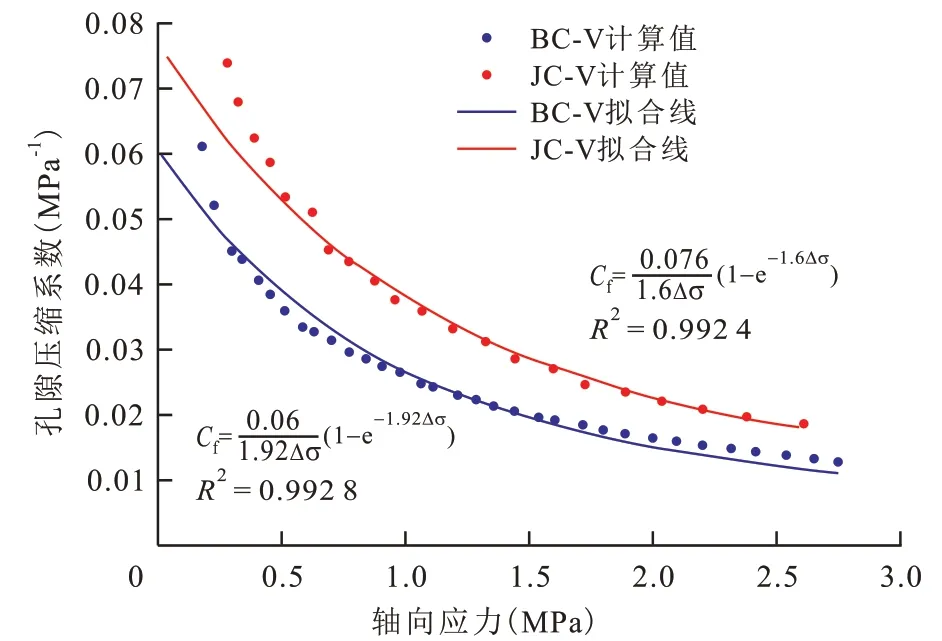
图6 煤样孔隙压缩系数随应力变化的拟合结果Fig.6 Fitting results of variations of pore compressibility of coal samples with stress

3.2 变孔隙压缩系数火柴束模型对孔渗-应力变化的拟合

应用改进火柴束模型（（14）和（15）式）对求得的孔隙度/渗透率和轴向应力之间的数量关系进行拟合，显示拟合度较高（图7），既证明由耦合应变的孔渗模型求得的孔渗参数与应力之间存在负指数关系，也表明改进的火柴束模型考虑孔隙压缩系数动态变化，更能够真实反映孔渗变化规律。

图7 煤样孔隙度和渗透率随应力变化的拟合结果Fig.7 Fitting results of variations of porosity and permeability of coal samples with stress

3.3 基于恒定/变化孔隙压缩系数的孔渗-应力规律对比

对比传统火柴束模型与改进的火柴束模型求得的孔渗参数发现（图8），在传统火柴束模型下，即定孔隙压缩系数下，孔隙度和渗透率随应力增加下降迅速，很快降低到较低水平；在改进的火柴束模型下，即变孔隙压缩系数下，孔隙度和渗透率随应力增加下降缓慢，并保持在较高水平；在初始应力段，2 种情形下的孔渗降低速率相当，而随着应力继续增大，定孔隙压缩系数下的孔渗降低速率开始超过变孔隙压缩系数下的孔渗降低速率，2 种情形下的孔渗差异越来越大。这是由于孔隙压缩系数固定意味着煤储层的致密程度在不同应力环境下均保持一致，应力增大必然导致越来越多的空间体积被压缩，孔隙度和渗透率急剧下降；而孔隙压缩系数变化意味着煤储层在不同应力环境下呈现不同的致密化程度，低应力条件下储层致密化程度低，受压缩的空间体积大，随应力增加，孔渗参数的降低速率较快；高应力条件下储层非常致密，应力增加引起的压缩空间体积有限，随应力增加，孔渗参数的降低速率也随之放慢。理论分析表明:低地应力背景下，采用定孔隙压缩系数求得的孔渗参数与采用变孔隙压缩系数求得的孔渗参数相近；而高地应力背景下，若还用定孔隙压缩系数计算，则会产生较大误差，有可能会将实际物性条件较好的煤储层误判为失去开发价值，从而影响到煤层气藏的整体开发效果。

图8 孔隙压缩系数恒定或变化时煤样孔隙度和渗透率随应力变化趋势Fig.8 Porosity and permeability variations of coal samples with stress under constant or changing pore compressibility

4 结论

随轴向应力增大，煤样的轴向应变曲线初始下凹，之后接近直线，表现为压密和弹性变形2个阶段特征；径向应变线性增加，体现出煤岩沿层理方向的非均质性相对较弱。

基于单轴力学形变理论，从孔隙度的定义式出发，建立了耦合力学应变的孔隙度、渗透率模型，该模型简化了参数配置，但应用限于低应力条件下且煤岩没有发生塑性变形破裂。通过模型求得的孔隙度、渗透率随轴向应力增大缓慢降低。

在变应力环境下，煤岩的孔隙压缩性发生改变，孔隙压缩系数随应力增加而减小，储层致密化程度增大，应力敏感性减弱，从而引起孔隙度和渗透率对应力的响应减弱，衰减幅度减小。评判煤储层物性时要考虑到孔隙压缩系数的动态变化，以确定合理的孔渗物性参数。

符号解释

Ro，ran——平均随机镜质组反射率，%；Mad——空气干燥基下的水分，%；Aad——空气干燥基下的灰分，%；Vad——空气干燥基下的挥发分，%；FCad——空气干燥基下的固定碳，%；V——镜质组，%；I——惰质组，%；E——壳质组，%；M——矿物，%；φo——初始孔隙度，%；Ko——初始渗透率，mD；L——样品长度，cm；D——样品直径，cm；εa——轴向应变；Δh——轴向长度减小量，mm；h——煤样长度，mm；εr——径向应变；Δr——径向半径增加量，mm；r——煤样半径，mm；εv——体积应变；ΔVb——应力作用下煤样的体积变化量，mm3；Vbo——煤样的初始总体积，mm3；φ——变形后的孔隙度；Vp——变形后的孔-裂隙体积，mm3；Vb——变形后的煤样总体积，mm3；Vpo——变形前的初始孔-裂隙体积，mm3；ΔVp——孔-裂隙体积变化量，mm3；K——变形后的渗透率，mD；Cf——孔隙压缩系数——等温条件下孔隙度随应力的变化率，MPa-1；σ——应力，MPa；T——热力学温度，K；Cfo——初始孔隙压缩系数，MPa-1；γ——孔隙压缩系数的下降速率，MPa-1；Δσ——有效应力变化量，MPa；m，n，α，β——应力敏感指数。