动态双足机器人建模及步态优化设计

陆万荣，许江淳，王志伟，任 杰

(昆明理工大学信息工程与自动化学院，云南 昆明 650500)

0 引言

目前，双足机器人是人工智能领域的一大研究热点。与传统的轮式、履带和爬行机器人相比，它对行走环境适应性好、能耗低、灵活性高，在医疗、教育、危险工业、航空航天和服务业等领域具有良好的应用前景和使用价值[1]。因此，国内外相关机构对双足机器人相关特性展开了深入研究，如Goswami教授提出了Compass-like机器人模型，进行了数值仿真和动态分析[2]；密歇根大学的Park等人实现了Rabbit机器人的动态行走等[3]。从1968年早稻田大学的WAP系列机器人到2006年WABIAN-2R机器人，再从美国的COG机器人到中国的BHR机器人，经过几十年的发展，尽管取得了不错的研究成果，但这一领域仍然有许多难以解决的问题，如稳定性、能耗和柔韧度等。

本文通过对机器人的稳定性和能耗寻优，建立多目标进化函数，实现机器人的稳定行走。以质心、步行周期、步行单元和步长等参数来描述双足机器人的行走过程。在寻优过程中，利用改进的扩展遗传算法(strength pareto evaluation algorithm，SPEA)，从稳定性和能耗两个方面进行计算，得到仿真需要的相关参数。在仿真过程中，与文献[4]中的原始倒立摆规划方案和文献[5]中提到的遗传算法优化方案进行比较，验证了本文所述方案的有效性。

1 D-H坐标法双足机器人建模

1.1 位置和姿态的坐标描述

双足机器人简化多连杆模型如图1所示。

图1 双足机器人简化多连杆模型

D-H建模方法是在机器人每根连杆上都建立一个坐标系，以4×4的齐次变换矩阵表示相邻连杆之间的坐标关系[6]。建立好坐标系后，则空间中的任意一点都可以用一个3×1的位置矢量来表示。位置矢量Ap在直角坐标系{A}中可以用3×1的列向量表示为：

Ap=[pxpypz]

(1)

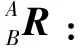
(2)

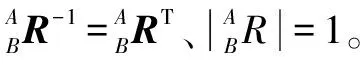
(3)

(4)

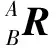
1.2 正运动学建模

正运动学是双足机器人仿真的基础，可以计算双足机器人的重心，描述双足机器人的空间姿态[7]。图1中，将双足机器人简化为只考虑踝关节、膝关节和髋关节的12自由度机器人，相邻自由度之间杆件视为均质的连杆，忽略连杆之间的摩擦力和间隙。每个连杆处的自由度均为独立的从属坐标系。

D-H模型参数见表1。

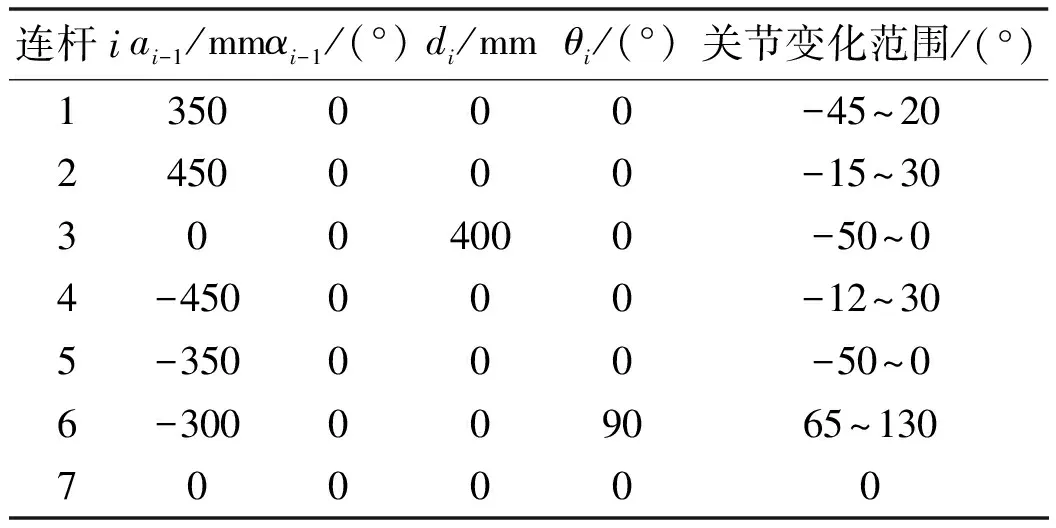
表1 D-H模型参数表

表1中：θi为垂直于关节i轴线的两个公垂线的夹角，即连杆夹角；di为沿关节i轴线的两个公垂线的距离，即连杆距离；ai-1两关节轴线沿公垂线的距离，即连杆长度；αi-1为垂直于αi所在平面内两关节轴线的夹角，即连杆扭角。

当连杆参数和坐标系确定后，依次左乘低一阶的变换矩阵，就能得到坐标系{i}对于起始坐标系的变换矩阵：

(5)

则:

(6)

(7)

1.3 逆运动学建模

逆运动学则与正运动学相反，已知相对于基础坐标系的位姿，根据连杆参数求各关节角度值[8]。在1.2节中已经把双足机器人简化为12自由度的连杆模型。根据机器人逆运动学理论，当自由度小于等于12时，逆运动学问题必有解且为点数值解。

本文计算逆解使用效率高、实时控制性好的封闭解法。求解思路是将位姿矩阵的逆矩阵按次序乘以正运动学方程，找出右端矩阵中的常数项与左端建立相等关系式，出现多解情况时，要根据实际情况合理选择。在求解之前，假设双足机器人身躯始终不倾斜，足底与地面水平接触。由踝关节、膝关节和髋关节行走时自由度之间的关系和假设条件，支撑腿和摆动腿的数学模型如图2所示。图2中：θ1=-θ3；θ2=0；θ4+θ5+θ6=0。

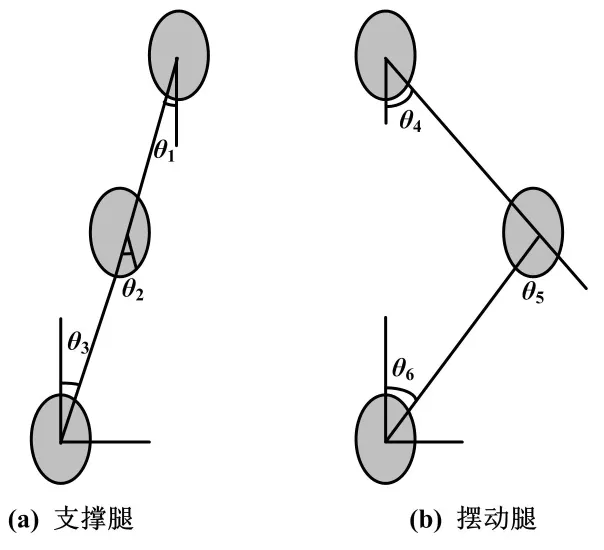
图2 支撑腿和摆动腿数学模型

建立等式：

(8)

将对应矩阵代入，就能得到如下关系式：

(9)

整理得：

pysinθ4

(10)

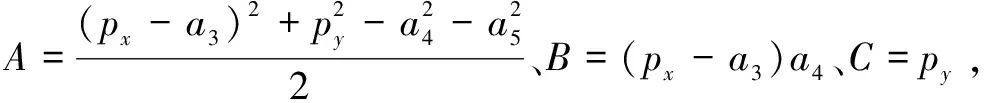
(11)

求得θ4后，根据下式求解θ5：

(12)

解得θ5=atan2(sinθ5,cosθ5),因此θ6=-(θ4+θ5)。

支撑腿的计算过程与上述方法一致，限于篇幅这里不再赘述，只给出结果：

(13)

2 步态优化设计

2.1 三维线性倒立摆

双足机器人是一个高阶、强耦合、非线性的复杂系统。对于这样一个复杂系统，可以先通过假设作一些简化处理：①将机器人所有部件质量看作一个支点；②倒立摆运动只限定在垂直地面的平面上；③以落脚点为支点，可绕其转动，连杆长度可调节[9-11]。

三维线性倒立摆(3D linear inverted pendulum,3D LIP)是目前双足步行规划中使用广泛的模型。三维线性倒立摆如图3所示。

机器人脚底在x、y、z所受力的分量为fx、fy、fz,所受力的力矩分量为τx、τy、τz。根据文献[11]提出的原理，能量消耗在力矩较小时变小，τx、τy均为0，那么可以将该模型简化为x轴、y轴方向两个部分。其运动方程如下：

(14)

解微分方程得到质心关于时间的函数：

(15)

(16)

只要知道了质心在x、y方向的初始位置和速度，就可以完成整个周期的质心(COM)规划。

图3 三维线性倒立摆示意图

2.2 多目标进化算法及改进策略

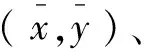
①髋关节的最大角速度ω_max与任意时刻关节j的最大角速度满足：

ωi(t)≤ωj_max

(17)

②质心到踝关节的长度与最大等效腿长满足：

(18)

式中：pos_z(t)、p_l(t)、p_r(t)分别为质心和左右踝关节的位置；ld2为最大腿长l_max的平方与髋关节到质心的距离d的平方之和。

③步行步长和步宽由l_max和zc约束，满足：

(19)

④设单步时间T内，髋关节转过的角度为q，有：

ω_maxT≤q

(20)

本文将问题抽象为多目标函数优化问题，分别得到关于稳定性和能耗的目标函数。

①质心到支撑腿中心的距离是影响机器人行走稳定性的重要因素，越靠近支撑中心越稳定。因此，稳定性目标函数表示为：

(21)

式中：x2、y2分别为x、y方向任意时刻t支撑中心与质心位置差值的平方。

②将摆动腿摆动的高度作为能耗大小的重要指标，能耗目标函数表示为：

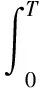
(22)

式中:z(t)为z轴方向摆动腿运动轨迹。

对以上目标函数的最优化问题，可以转换为构造惩罚函数对约束条件hi(x)的最小化问题。设惩罚函数为：

p(x,M)=M∑imin [0,hi(x)]2

(23)

M为惩罚因子，将约束条件带入目标函数，利用改进SPEA算法求解Pareto最优解集。设初始种群P的规模为N，存档集Q和局部存档集规模均为M。改进SPEA算法步骤如下。

①初始化种群P和存档集Q、L。

②计算P、Q和L中所有个体的适应度。

③将Pt、Qt、LT中的非支配个体保存到Qt+1中，若其规模不为M，则调整其规模满足分布要求。

④如果满足设置的停止条件，则将Qt+1中的非支配个体返回；否则继续。

⑤对Qt+1进行竞标赛选择。

⑥对Qt+1进行交叉、变异操作，并将结果保存至Pt+1，且更新Pt+1的部分个体，令t=t+1，继续步骤②。

3 虚拟样机仿真和分析

采用ADAMS和Matlab联合仿真进行仿真测试,ADAMS中可以建立逼真的三维模型，并具有动力学和运动学特性。通过相关接口将参数特性传递给Matlab/Simulink。后者又可以对步态进行规划，将规划好的步态信息通过控制模块再传递给ADAMS，从而建立起机器人的动态行走并且进行实时的性能分析评估。

3.1 双足机器人建模

双足机器人的各部分参数取值来自175 cm成年人体型特征，按一定的比例缩小选取。绘制小腿、大腿、脚部和上体质量块是需要通过边缘剪切、过孔/打孔的方式绘制对应关节的转动样式。而关节绘制时，为了满足步态规划的准确性，需要注意转动轴的个数；数量不同，绘制的复杂度就不一样。踝关节前向、侧向两个转动轴需要交于一点；髋关节前向、侧向和竖直三个转动轴也需要交于一点；而膝关节较为简单，只有前向俯仰一个旋转轴。建立好模型后，各部件之间仍然是相互独立的，需要在部件与连杆之间建立联系，在ADAMS中对不同部件添加约束，完成完整的建模过程。各部分和整体组合模型如图4所示。

图4 各部分和整体模型示意图

动态行走3D观测图如图5所示。

图5 动态行走3D观测图

3.2 仿真结果和分析

图6 角速度变化图

从图6可以看出，双足机器人侧向摇摆具有整体性和一致性。踝关节和髋关节角度变化情况相同，呈周期性变化。

CM、CM1、CM2分别表示本文优化方案、遗传算法优化方案和原始倒立摆方案左腿质心在前向、侧向、和竖直方向三个方向速度的变化曲线。通过对比，遗传算法方案前向速度变化范围较大，原始倒立摆方案存在明显突刺，而本文使用的方案变化情况较为折中。

左腿质心不同方向速度变化如图7所示。

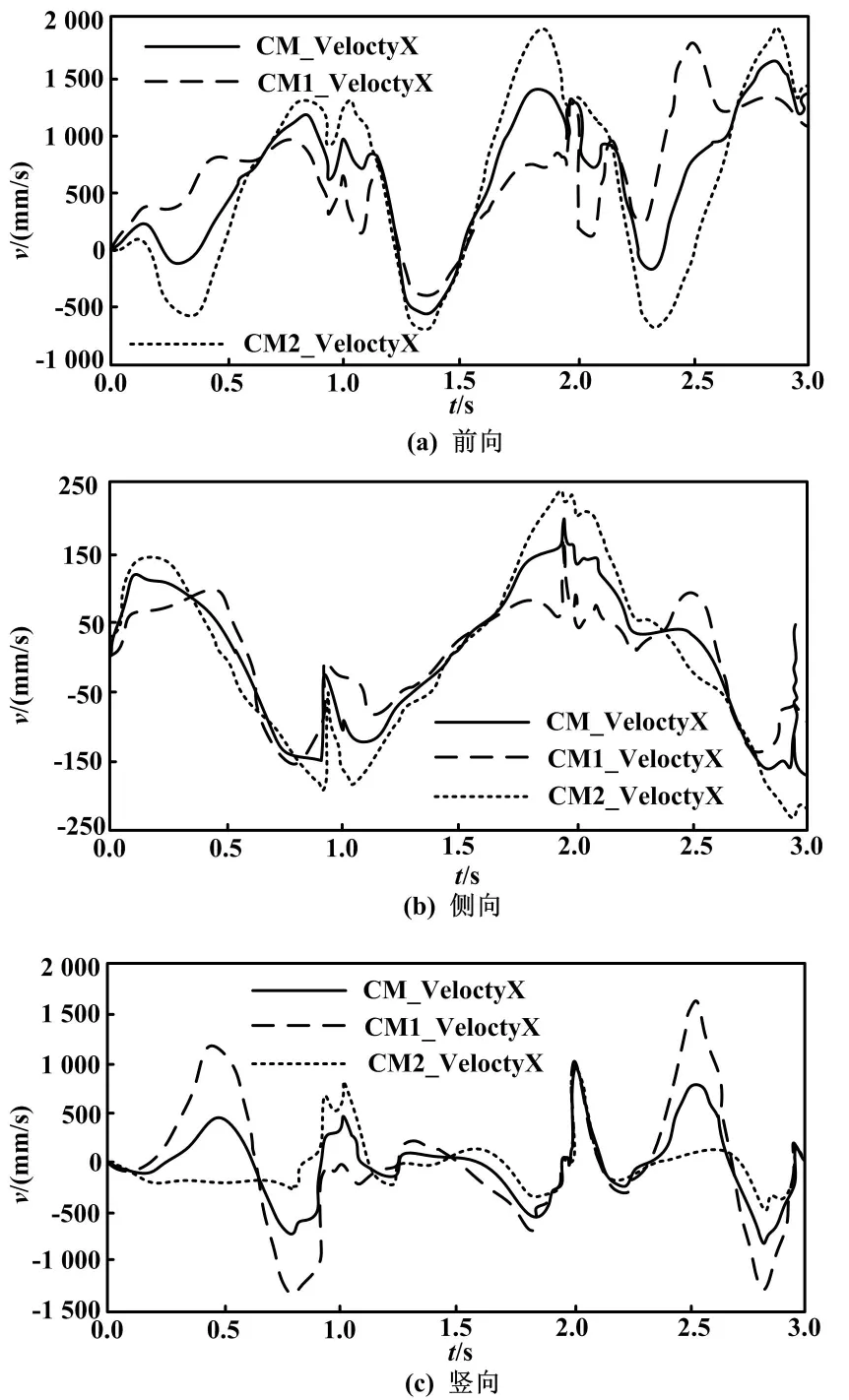
图7 左腿质心不同方向速度变化图

左腿质心前向加速度变化如图8所示。从图8可以看出，在摆动腿和支撑对互换时，加速度变化都比较明显，但是CM1和CM2产生的突刺幅度较大，对质心加速度的影响更大。

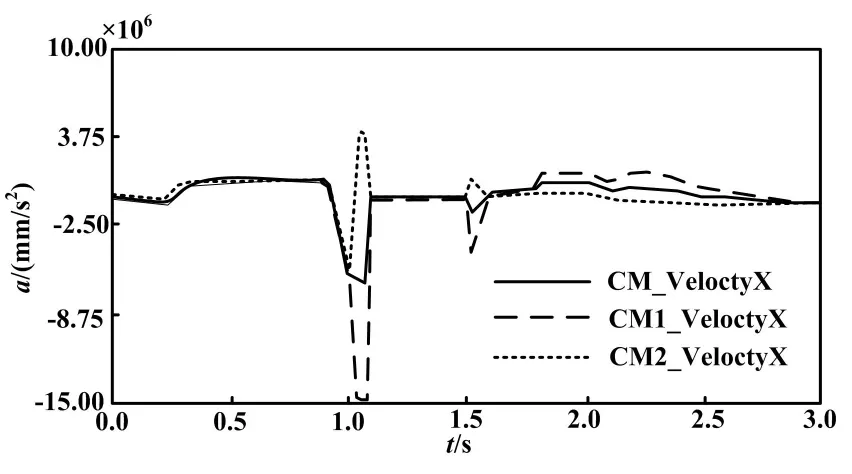
图8 左腿质心前向加速度变化图

4 结束语

本文对双足机器人的步态规划进行了仿真研究。先在双足机器人多连杆模型上进行D-H法正逆运动学建模。接着进行了步态优化设计，建立了以稳定性和能耗为目标的寻优函数，利用改进的SPEA算法解得最佳参数。最后利用得到的参数使用ADAMS/Matlab进行联合仿真分析，与原始倒立摆规划和遗传优化方案作对比。由双足机器人左腿质心在前向、侧向和竖直方向的速度和加速度对比结果可知，本文提出的优化方案变化幅度最为平缓，稳定性效果最优，可以为机器人步态规划方面的相关研究提供一定的参考。