空中微弱目标长时间相参积累技术研究
2019-12-04王志刚翟栋梁刁志龙
王志刚,洪 畅,翟栋梁,刁志龙
(中国船舶重工集团公司第七二四研究所,江苏 南京 211153)
0 引 言
不同于扫描体制的雷达,凝视雷达通常采用“单波束发射、同时多波束接收”的3D覆盖体制实现方位、俯仰全空域监视,因此可采用多脉冲长时间相参积累的方式,补偿低增益发射天线带来的信噪比损失,大幅提升杂波环境下的目标检测概率。但随着飞行器隐身技术和运动性能的发展,出现了大量以“低可观测、高机动性”为代表的空中微弱目标。该类目标的信杂噪比相对较低,而且运动轨迹复杂,使得传统相参积累检测算法基本失效。因此,如何增强此类目标能量并实现有效检测,已成为凝视雷达探测领域中的一个研究热点[1-2]。
不考虑雷达性能、体制等设计,仅利用信号处理手段实现微弱目标检测的有效办法即上述凝视雷达的多脉冲长时间相参积累方法。然而,在长时间积累过程中,由于目标的相对运动或系统距离分辨率较高,将导致目标回波散落于不同的距离单元中;同时,当目标在进行变速飞行时,其多普勒也是时变的。因此,对于高机动微弱目标而言,在单个波束照射期间难以收集到足够超过雷达检测门限的回波能量,必须将分散于多个波束中不同距离单元和不同多普勒通道的目标回波有效地积累起来,最终有效提高雷达对微弱目标的检测能力[3]。
本文首先详细介绍微弱运动目标回波信号特征,建立涵盖跨距离单元和多普勒通道走动的匀加速运动目标回波模型;然后基于Keystone变换[4]对雷达回波慢时间轴进行伸缩变换,从而消除回波的距离走动;最后基于高阶模糊函数法[5-6]对多普勒通道进行补偿和校正。实验结果表明,经过距离走动校正和多普勒通道补偿后,雷达检测性能显著提高。
1 匀加速运动目标回波模型
面向运动微弱目标多维特征探测的作战需求,基于线性调频波形,深入分析低慢小运动目标回波信号特征,建立涵盖跨距离、多普勒单元走动的有效回波模型,为定量分析低慢小目标检测所存在距离走动和时变多普勒问题及开展目标检测的总体设计提供理论基础和信号级模型支撑。
假设雷达周期地发射基带信号为线性调频(LFM)的脉冲信号[7],其形式为:
(1)

雷达通过载频fc发射LFM 脉冲信号,其发射信号st(t)的形式为:
st(t)=p(t)exp(j2πfct)=
(2)
假设一个运动目标的径向速度为v,径向加速度为a,初始距离为R0,则目标运动模型可以由下式表示:
(3)
则二维回波数据可以表示为:
(4)
式中:c为光速;λ为波长。
经过脉冲压缩后,回波可以写成:
(5)
式中:A为脉压后回波的复数幅度,仅考虑非起伏情况下,A是一个常数;B为信号的带宽。
将式(3)代入式(5),则有:
(6)
所以,需要处理的信号是一个二维矩阵:快时间维和慢时间维。该二维矩阵中包含了目标的距离和多普勒信息,雷达检测处理的主要目的就是要从这个二维矩阵中提取出目标的有用信息。
2 相参积累检测
微弱目标的长时间积累会对回波信号带来很大影响:一方面,不同重复周期的回波信号包络会出现距离走动现象;另一方面,回波信号己经不是单频信号,而是多项式相位信号,从而导致多普勒时变现象。这2点都会严重影响相参积累的效果,导致传统检测方法的性能下降。本节以匀加速运动目标为对象,详细研究了同时存在距离走动和多普勒频率时变现象时信号的相参积累与检测方法。
2.1 距离走动校正
在长时间积累过程中,由于积累时间较长且雷达距离分辨率的提高,致使目标可能在多个距离单元间走动。严重的距离走动将导致目标回波能量散落在众多距离单元,而使传统相参积累算法无法积累。因此,利用基于先校正距离走动再相参积累的Keystone 变换法实现跨距离走动弱小目标的积累检测。
Keystone变换是合成孔径雷达(SAR)中常用的距离走动校正技术,后逐步将该变换用于微弱目标检测中。Keystone 变换实际上是通过对慢时间轴的伸缩变换,将雷达回波的矩形支撑域变换成一个倒梯形,如图7所示,从而消除回波的距离走动。

图1 Keystone变换
假设雷达发射信号模型如第1节所述,并把式(5)重写如下:
(7)
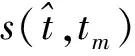
(8)
(9)
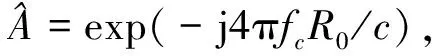
可以看到,在频率域,慢时间维产生的多普勒频率不仅与信号的载频、目标的径向速度和径向加速度有关外,与快时间维的信号频率也有关系。所以,包络中心的距离走动,反映在频域上,就是慢时间tm和快时间的信号频率f之间存在的耦合。Keystone变换进行距离走动校正的基本思想就是利用尺度变换,在频域消除两者之间的耦合,反映在时域上即是完成了对距离走动问题的校正。
定义一个虚拟时间τm,τm与tm的关系如下:
(10)
将式(10)代入式(9),得:
(11)
观察式(11)可知,经过变量代换引起回波距离走动的指数项已消除,相应的目标回波的距离走动也得到补偿。然而,雷达是沿着慢时间tm轴以Tr为周期进行采样的,而τm时刻实际上没有采样值,且τm的取值还与f有关。因此Sτm(f,τm)的取值应当在S(f,tm)平面通过插值得到。在多普勒频率存在模糊的情况下,需要知道多普勒模糊程度后才能实现正确的插值。经过距离走动补偿后,目标回波集中于相同的距离单元,随后就可采用传统的相参积累算法。
2.2 多普勒通道补偿
目标的多普勒频率往往是变化的。一方面,由于目标存在加速度等运动分量,使得其运动速度是时变的,与之相对应的多普勒频率也是时变的;另一方面,在长时间对运动目标观测时,目标运动方向与雷达的视线夹角也在不断变化,这使得即使是匀速运动目标其多普勒频率也在发生变化。因此,无论是对匀速目标进行长时间相参积累检测,还是对机动目标进行检测,只有对目标回波相位进行必要的补偿,消除跨多普勒走动,才能在信噪比较低的情况下检测到微弱目标。
高阶模糊函数法(HAF)又称为多项式相位变换法(PPT),是检测多项式相位信号最简单也最经典的算法之一[8]。其主要思想就是引入一个非线性变换(HIM),将多项式相位信号转换成一个单频信号,再对这个单频信号做傅里叶变换,即可估计出信号的最高阶相位系数。
信号s(t)的M阶瞬时矩(HIM)定义为:
(12)
对其瞬时矩进行傅里叶变换即可得到高阶模糊函数的定义:
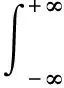
(13)
若信号为M阶多项式相位信号,则:
(14)
s(t)的M阶瞬时矩为一单频信号:
sM(t;τ)=A2M-1exp[j2π(b1t+b0)]
(15)
式中:b1=M!τM-1aM;b0=(M-1)!τM-1aM-1-0.5M!(M-1)!τMaM。
由式(15)可以看出,单分量M阶多项式相位信号的M阶瞬时矩为一个单频信号。对其进行傅里叶变换,可得其M阶模糊函数为:
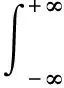
A2M-1δ(f-b1)
(16)
所以,s(t)的M阶模糊函数会在b1处能量汇聚。根据模糊函数能量汇聚的b1,可以估计出多项式相位信号的阶数M和最高阶系数aM。
对于匀加速运动目标而言,当距离走动被校正之后,由于高阶相位的存在,信号的多普勒频率是随时间线性变化的,对于同一距离门的慢时间来说,信号可以表示为:
(17)
由式(17)可以看到,经过距离走动的校正后,对于慢时间维来说,要处理的实际上就是一个离散的线性调频信号,其频率fd与目标的径向速度有关,而调频率k与目标的径向加速度有关。所以,可以采用线性调频信号的参数估计和检测方法,对慢时间维信号进行处理。
(18)
所以,其二阶模糊函数为:
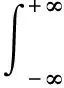
A2δ(f-Kτ)
(19)
由式(19)可以得到,线性调频信号的二阶模糊函数是一条过原点的直线,直线的斜率即为线性调频信号的调频率。示意图如图2所示。

图2 LFM模糊函数示意图
对于固定的τ,线性调频信号的二阶模糊函数在f=Kτ处有峰值点,因此可以根据这个峰值估计出线性调频信号的二次相位。得到二次相位系数之后,就可以进行相位补偿。
因此,可以将高阶模糊函数法用于变速运动目标回波慢时间信号处理中。首先估计出慢时间信号的调频率,对慢时间维信号进行相位补偿,将时变多普勒频率信号变为单频信号,之后再进行快速傅里叶变换(FFT),即可实现脉冲的相参积累。
2.3 运动补偿处理流程
综合考虑雷达的相参积累脉冲数、相参积累时间和微弱目标的运动速度及加速度情况,为提高相参积累得益与微弱目标检测概率,解决跨距离单元和跨多普勒单元走动问题,采用如图3所示的先跨距离单元补偿、后跨多普勒单元补偿的处理流程。
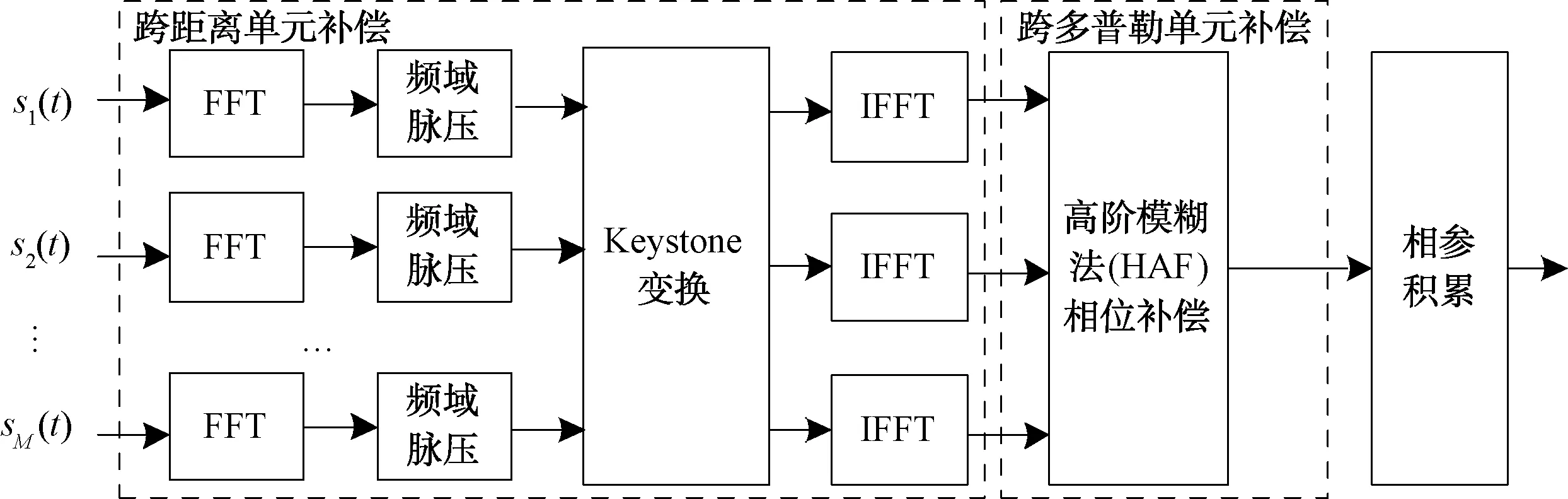
图3 精细化运动补偿处理流程
3 实验结果分析
通过仿真实验验证基于Keystone变换距离走动校正方法和基于高阶模糊函数的跨多普勒单元补偿方法的有效性。仿真参数设置如下:初始目标径向速度v=400 m/s,径向加速度a=30 m/s2,雷达发射载频fc=10 GHz,信号带宽B=20 MHz,脉宽Tp=20 μs,脉冲重复频率FPRF=7.5 kHz,快时间域采样频率50 MHz,相干积累脉冲数N=1 000。
3.1 距离走动校正
图4给出的是脉压后信噪比为2 dB时,涵盖跨距离单元和多普勒通道走动的匀加速运动目标回波模型仿真结果图。由图4可知,在长时间积累过程中,目标回波数据经脉压后,横跨20个距离单元,严重的距离走动导致目标回波能量散落在众多距离单元,而使传统相参积累算法无法积累。
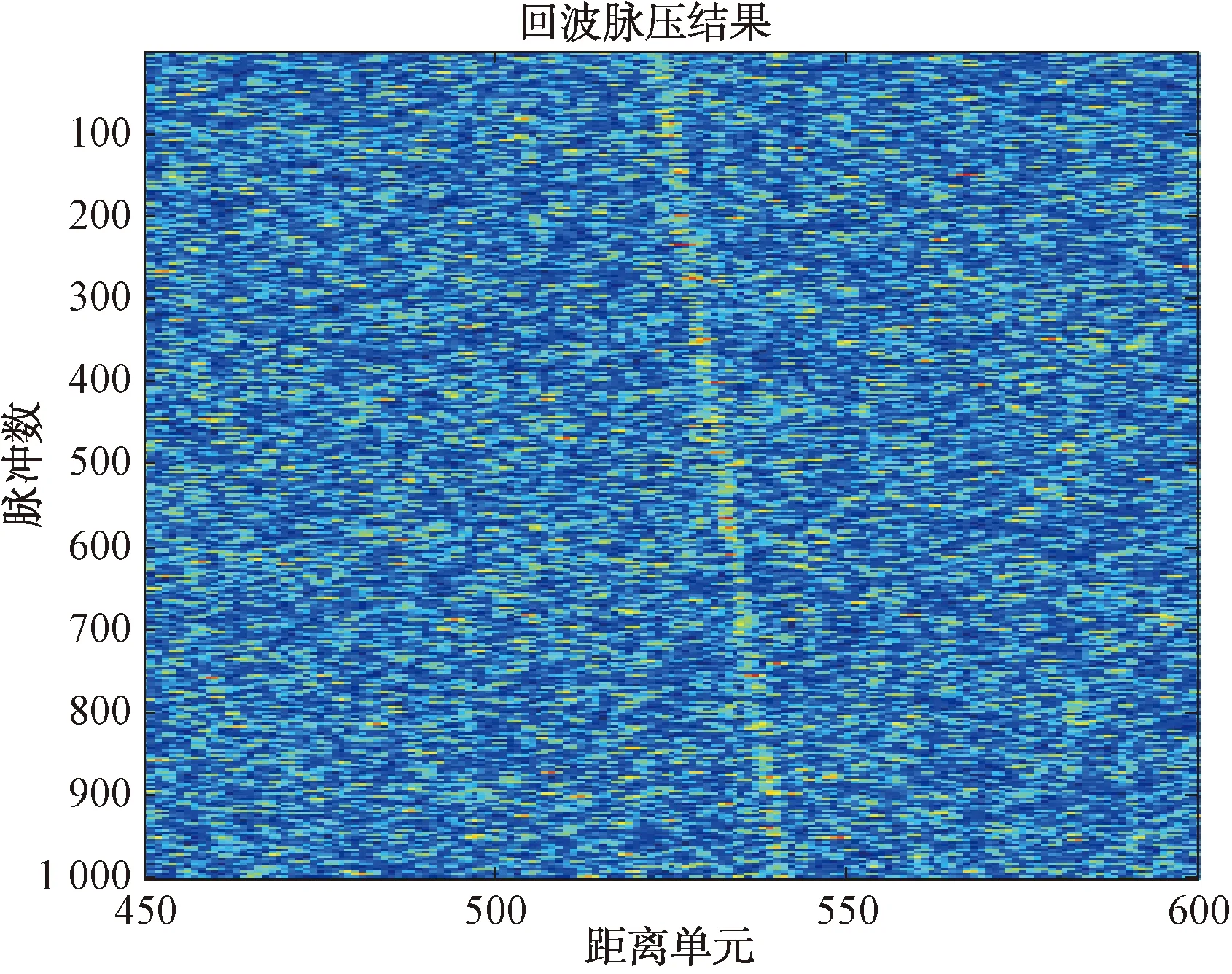
图4 匀加速模型下回波脉压结果
图5给出的是基于Keystone变换的跨距离走动校正脉压结果。由图5可知,经过距离走动补偿后,目标回波集中于相同的距离单元。

图5 跨距离走动校正脉压结果
3.2 多普勒通道补偿
由图6可以看到,经过Keystone变换之后,信号在距离单元上的能量有所聚集,但由于加速度项对多普勒频率的影响,信号在经过FFT之后,在多普勒域能量并没有很好地汇聚,出现了多普勒扩散现象,如图6所示,回波能量散落于不同多普勒通道将降低雷达对微弱目标的检测能力。

图6 匀加速模型下跨多普勒走动结果
只有对目标回波相位进行必要的补偿,消除跨多普勒走动,才能在信噪比较低的情况下检测到微弱目标。如图7所示,目标能量集中在同一个多普勒单元内,消除了多普勒扩散。并且积累后的目标能量集中在一个距离单元和一个多普勒单元内,通过二维恒虚警检测,可有效检测出目标。
4 结束语
本文建立涵盖跨距离单元和多普勒通道走动的匀加速运动目标回波模型,然后基于Keystone变换消除回波的距离走动,基于高阶模糊函数法对多普勒通道进行补偿和校正。实验结果表明,经过距离走动校正和多普勒通道补偿后,雷达检测性能显著提高。该类算法除了适用典型的长时间相参积累场景,还适用于目标超高速运动和雷达高分辨等场景。然而,一方面,大量的插值操作会影响基于Keystone变换的相参积累算法的执行效率;另一方面,不考虑多普勒模糊程度就进行插值,会降低脉冲相参积累的峰值,不利于信噪比的改善,有待进一步研究。
