自然电场三维有限元正演模拟
2019-12-03周竹生朱海伦刘思琴
周竹生,朱海伦,谢 静,刘思琴,杨 阳
(1.中南大学 地球科学与信息物理学院,长沙 410083;2.山西省煤炭地质物探测绘院,山西 晋中 030600)
起伏地形对地表电位分布的影响较大,研究起伏地形引起的电位假异常是电法勘探理论发展的需要[1-4]。目前直流电法二维正反演技术已相当成熟,也开展了大量的三维正反演研究工作并取得了显著成果;但复杂地形条件下的三维正反演研究仍有探索空间。正演是反演的基础,开展快速、高精度的正演模拟工作,有助于反演技术的发展。常规的正演模拟方法,如有限单元法、有限体积法、有限差分法等,通过简化实际地电模型实现正演模拟过程,以更好地认识地下异常体的地表异常响应。其中有限单元方法模拟精度高、求解简易且规范、自动满足内部边界条件,适于各种复杂的物性分布情况,是一种实用高效并应用广泛的正演模拟方法[5-9]。
单元网格剖分是正演模拟的核心工作,研究网格剖分方法对建立有限元模型至关重要。目前常规的结构化网格剖分技术仍以六面体为基础单元。规则六面体剖分只适用于水平地形条件下的三维正演模拟,一定程度上限制了三维有限元的发展和应用。熊彬等首先提出先将研究区域进行一级六面体剖分,再将六面体二级剖分为6个四面体,对四面体添加地形数据,以完成三维复杂地形条件下的有限元正演模拟[10];在此基础上,吕玉增等提出一种四面体网格交叉剖分技术,并将六面体的二级剖分减少为5个四面体[11]。但以上两种剖分技术必须满足四面体单元交叉分布,才能保证模拟误差呈对称性分布。强建科提出任意三棱柱单元剖分方式,该三棱柱包含地形特征,能有效贴合起伏地形,成功实现复杂地形条件下的三维有限元正演模拟[12];但该剖分技术必须满足模型的顶底界面平行,不利于模型的建立,且对模拟精度有一定影响。
本文基于前人研究,提出一种新的三维有限元结构化网格剖分技术,该技术先将研究区域一级剖分为规则六面体,再将六面体二级剖分为4个三棱柱,最后将每个三棱柱三级剖分为3个四面体。该剖分技术综合了三棱柱剖分和四面体剖分的优点,能更好地贴合复杂地形,且有效解决了剖分方式引起的模型底界面畸变以及误差不对称分布等问题;同时在研究区域一定、六面体网格尺度一定时,模拟得到的节点信息更为丰富,模拟精度更高。
本文首先通过均匀半空间三维点源模型进行算法验证,同时建立渗流自然电场地电模型,探讨分析渗流走向以及起伏地形对地表自然电位分布的影响。
1 网格剖分技术
1.1 常规结构化网格剖分技术
常规六面体网格剖分技术是最简单易行的三维剖分方式,但其最大缺陷是不能实现复杂地形条件下的三维模拟。熊彬等[10]将研究区域先剖分为规则六面体,然后将每个六面体单元再二次剖分为6个四面体单元以添加高程数据(图1);吕玉增等[11]提出的四面体网格交叉剖分技术是将六面体网格中的四面体网格减少到5个(图2);强建科[12]提出的任意三棱柱网格剖分技术能较好地贴合起伏地形,但每个三棱柱单元都必须满足上、下底面平行相等(图3),故而该剖分技术会致使整个研究区域的顶底边界完全平行相等,从而使得整个研究区域的空间结构变得畸形,将对模拟精度产生一定影响。以上剖分技术有一个共同的缺陷,即每个六面体单元的上顶面划分为2个三角形时(图4),会导致计算误差分布不具对称性。虽然吕玉增等[11]提出的交叉剖分技术能解决对称精度问题,但该过程不易于程序实现。
1.2 新结构化网格剖分技术
综合考虑以上几种常规的三维有限元结构化网格剖分技术的优缺点,本文提出一种新的剖分技术,集以上所有剖分方式的优点于一身,同时摒弃了上述剖分方法的所有缺陷。该剖分方式是将1个六面体先剖分为4个三棱柱,然后再将各三棱柱二次剖分为3个四面体,即将1个六面体剖分为12个四面体,相应单元节点数由8增加到10(图5)。相比传统的结构化网格剖分技术,新剖分技术在六面体顶底面各增加了一个中心节点,在研究区域一定、六面体剖分网格一定时,能有效提高正演模拟精度,同时保证了计算误差呈对称性分布,且不用考虑复杂的交叉剖分问题,便于编程实现。

图1 六面体单元剖分为6个四面体Fig.1 A hexahedral element is subdivided into six tetrahedrons

图2 六面体单元剖分为5个四面体Fig.2 A hexahedral element is subdivided into five tetrahedrons

图3 六面体单元剖分为三棱柱网格单元Fig.3 Hexahedral elements are subdivided into triangular prism elements

图4 常规六面体上顶面剖分方式Fig.4 Top surface subdivision of hexahedron elements
2 有限单元法
2.1 三维点源场边值问题
均匀半空间三维点源模型(图6),电位满足微分方程[13]
▽·(σ▽u)=-2Iδ(A)
(1)
其中:σ为电导率;u为电位;I为点源电流;δ(A)为关于场源所在位置A点的δ函数。
在地表Г上满足
∂u/∂n=0
(2)
在近似无穷远边界Г∞上,取混合边界条件
(3)
其中:n为边界外法向单位向量;r为点源指向边界Г∞上任一点的向量,而区域内部电导率边界为自然边界条件,不予考虑。

图5 新剖分技术的剖分过程Fig.5 The subdivision process of the new subdivision technology

图6 均匀半空间点源模型Fig.6 3D point source model in homogeneous half-space
2.2 四面体单元分析
与三维点源模型边值问题等价的变分问题为
(4)
在四面体单元中(图7),空间坐标x、y、z及电位u的插值函数为
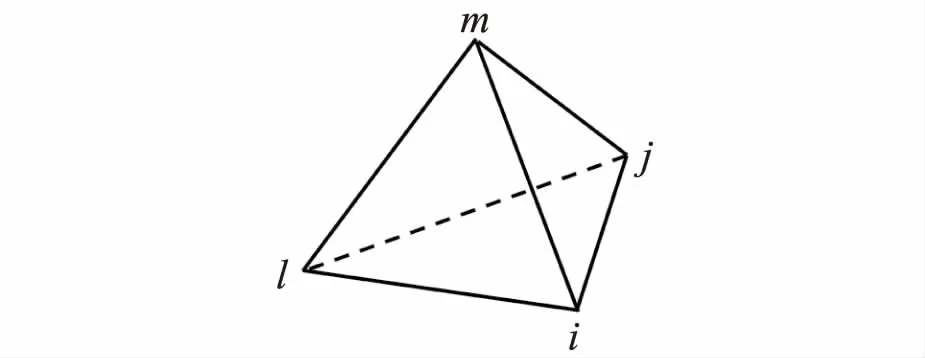
图7 四面体单元Fig.7 Tetrahedral element

(5)
式中:Ψ分别为x、y、z;Nk为形函数,且Nk=(ak+bkx+cky+dkz)/(6Ve),其中ak、bk、ck、dk具体表达式见文献[14],k=i,j,l,m;而Ve为四面体体积。
对全域进行剖分,将变分问题的积分分解为各单元e上的积分。对体积分项有
(6)
整理得到四面体单元体积分矩阵为:K1e=(kij),其中kij=σ(bibj+cicj+didj)/(36Ve)。
对于边界积分,近似cos(r,n)及|r|为常量,将其提到积分号外,整理得到边界积分为
(7)
其中:K2e为边界积分系数矩阵[14];ue为单元节点电位向量。
对全体节点组成的矩阵有

(8)

3 正演模拟
3.1 算法验证
本节通过建立均匀半空间点源模型进行算法验证。模型空间剖分为30×30×30个六面体网格单元,区域大小取60 m×60 m×30 m,点源置于地表中心。将各个六面体单元分别按图4的2种剖分方式以及本文提出的新剖分技术进行剖分,实现不同剖分方式的正演模拟。考虑点源奇异性,图8所示为地下2 m深处的电位等值线平面,正演结果表明剖分方式对计算精度有一定影响,单一朝向的剖分技术会使得本应呈对称性分布的地表电位失去对称性。
3.2 误差分析
为进一步说明新剖分技术对模拟精度的影响,将图8中的3个电位平面分别与解析解作误差分析,剖分方式的不同导致误差分布存在较大差异(图9)。单一朝向的剖分方式使得误差不再关于点源呈对称分布,而是具有方向性(呈轴对称分布)。本文提出的剖分方式,能保证误差对于点源呈对称分布,且模拟精度更高。
3.3 渗流自然电场地电模型
自然电场法无需供电,仪器设备轻便,生产效率较高,在传统的矿产与油气勘探[15]、地热火山调查[16-17]、地震观测[18-19]等领域得到广泛应用,近年来还在工程与环境[20-24]等新兴领域得到广泛应用。流动电位是基于电动机理产生的自然电位,其在自然条件下普遍存在,在工程和地下水地球物理学中受到广泛关注。它为检测水坝、水库地面、排水结构渗漏等问题提供了一种经济有效的手段,还可以用于监测含水层中的水运动、山体滑坡、垃圾填埋场污染泄漏等问题。有针对性地开展流动电位正演模拟研究将有助于反演解释,更好地提高该方法的应用效果。利用本文提出的结构化网格剖分技术,实现流动电位三维正演模拟,探讨分析起伏地形以及渗流方向引起的地表自然电位异常特征。

图8 深度为2 m处的电位等值线图Fig.8 Electric potential contour maps at the depth of 2 m(A)六面体顶面向左倾斜;(B)六面体顶面向右倾斜;(C)新剖分技术

图9 不同剖分方式的相对误差Fig.9 Relative error of different subdivision techniques(A)六面体顶面向左倾斜;(B)六面体顶面向右倾斜;(C)新剖分技术
直立渗流模型如图10所示。2个模型大小均为100 m×100 m×100 m,渗流通道位于中部,在模型(B)中添加正负地形。通过正负离散点源近似模拟渗流场的电荷分布,数值模拟结果如图11、图12。正负地形对地表电位分布均有一定影响:因正地形使得电位衰减距离变长,故异常幅度减小;而负地形等效于电位衰减距离变短,故异常振幅增大。

图10 三维模型的二维剖面Fig.10 2D subsurface structures of 3D models(A)直立渗流无地形;(B)直立渗流带正负地形
倾斜渗流模型如图13所示。模型大小为100 m×100 m ×100 m,渗流口位于模型中部,以3个不同倾角(0°、30°、45°)向地下渗流。以正负离散点源近似模拟渗流场的电荷分布,模拟结果如图14、图15。倾斜渗流走向会引起地表电位的不对称分布:在渗流方向上能观测到自然电位正异常,且随着倾角的增大,即渗流通道越趋于水平,所观测到的正异常越大。据此可有效判断地下渗流走向,可应用于地下水监测、追踪地下污染渗流等。

图11 地表自然电位等值线图Fig.11 Contour maps of ground self-potential

图12 主剖面地表自然电位曲线Fig.12 Ground self-potential curves of main profile

图13 倾斜渗流模型的二维结构Fig.13 2D subsurface structure of inclined seepage model

图14 地表自然电位等值线图Fig.14 Contour maps of ground self-potential (A)倾角0°;(B)倾角30°;(C)倾角45°

图15 主剖面地表电位曲线Fig.15 Ground self-potential curves of main profiles
4 结 论
本文从网格剖分技术出发,分析总结了几种常用的三维结构化网格剖分技术的优缺点,并提出一种新的三维结构化网格剖分技术;然后结合三维点源场边值问题,推导了四面体有限单元基本方程,并对比分析了几种剖分技术的模拟精度;最后实现了渗流自然电场地电模型正演模拟,探讨了渗流走向以及正负地形对地表自然电位分布的影响。
在算法方面,该剖分技术具有网格单元呈对称性分布的特点,同时易编程实现,不用考虑网格交叉技术的繁琐过程;在正演模拟结果方面,该剖分技术能完美解决常规结构化网格剖分技术中的误差非对称性问题,同时在一定程度上提高了模拟精度。由渗流自然电场正演模拟结果可知,正地形使电位异常幅度减小,而负地形使电位异常振幅增大;在渗流方向上能观测到较大的正异常,有助于确定渗流走向。
需要说明的是,本文提出的剖分技术在一定程度上增加了单元节点数,增加了计算量,但计算精度也更高。当今计算机性能高速发展,以较少的计算增加量换取更高的计算精度是有一定实际意义的,在选择剖分技术时,综合考量侧重点即可。
