A Modified Cohesive Zone Model for Simulation of Delamination Behavior in Laminated Composites

WU Yitao，LIAN Wei

1. Shanghai YS Information Technology Co.，Ltd. Shanghai 200240，P.R. China；

2. Shanghai Aircraft Design and Research Institute，Shanghai 201210，P.R. China

（Received 21 September 2018；revised 25 March 2019；accepted 2 July 2019）

Abstract: Considering the promotion effect of interlaminar normal tensile stress and the inhibition effect of interlaminar normal compressive stress，two kinds of elimination initial criteria were proposed in this paper. Based on these two delamination initial criteria，a modified cohesive zone model （CZM） was established to simulate the delamination behavior in laminated composites. Numerical simulations of double cantilever beam（DCB），mixed -mode bending（MMB）and end notched flexure（ENF）tests were conducted. The results show that the proposed model can do a better job than common ones when it is used to predict laminates’delamination under interlaminar compression stress. Moreover，a factor r，named cohesive strength coefficient，was defined in this paper on account of the difference between cohesive strength and interlaminar fracture strength. With changing factor r，it shows that a moderate variation of cohesive strength will not cause significant influences on global load - displacement responses.Besides，in order to obtain a good balance between prediction accuracy and computational efficiency，there shall be two or three numerical elements within the cohesive zone.

Key words: composite laminate; delamination; numerical analysis; cohesive zone model

0 Introduction

Delamination is a common failure mode of composite materials. For the past few years，cohesive zone model（CZM）approach has been increasingly used to conduct numerical simulation of delamination damage［1-10］. The CZM approach assumes that there exists a cohesive damage zone ahead of the crack front. Within the cohesive damage zone，the constitutive relationship can be described by cohesive tractions and corresponding relative displacements between two separating surfaces. Both the onset and the non-self-similar propagation of delamination can be directly predicted by CZM approach，which avoids the tedious re-meshing during fracture mechanics approach.

There are five primary characteristic parameters of cohesive zone model：initial interface stiffness， delamination initiation criterion， cohesive strength，critical energy release rate and shape of Tδ curve. Generally，the critical energy release rate is regarded as the material constant and can be determined by fracture toughness tests. The initial interface stiffness of cohesive zone shall be determined to meet the following two principles. First，it cannot significantly influence the whole structure stiffness.Second，enough rigid connection between two adjacent layers shall be ensured before delamination initiation. Among all delamination initiation criteria，quadratic stress-based criterion is the most commonly used one［1-2，4，9，11］. This criterion involves the promotion effect on the initiation of interlaminar fracture caused by normal tensile stress，but ignores the inhibition effect caused by normal compressive stress. The cohesive strength refers to the critical stress field intensity at crack tip when delamination initiates. The cohesive strength is usually assumed to have the same value with the interlaminated fracture strength in most papers［1-2，4，7，9］，but there are different in terms of the physical nature［12］. The traction-relative displacement curve（T-δ curve）can be represented by different functions：the bilinear function［1-4，6-7，9，13-14］， trilinear function［15］， trapezoidal function［16］，exponential function［5，10，17］and the polynomial function［8］. However，the simplest bilinear traction-relative displacement curve has been widely used to describe the constitutive relationship of cohesive zone.

In this paper，a modified cohesive zone model was proposed to simulate laminates’delamination.Both the promotion effect on delamination initiation caused by normal tensile stress and the inhibition effect caused by normal compressive stress were involved. A new factor，cohesive strength coefficient r，was defined in present model. Through changing coefficient r，influence of cohesive strength on structure’s global load-displacement response was investigated. Meanwhile，influence of the mesh size within cohesive zone length was also analyzed. According to this modified cohesive zone model，simulations of double cantilever beam（DCB），mixed -mode bending（MMB） and end notched flexure（ENF）tests were conducted. By comparing numerical results with experimental data，the rationality of this modified model is shown.

1 Modified Cohesive Zone Model

1. 1 Delamination initiation criteria

Under the inspiration of Mohr - Coulomb fracture theory，we thinks that delamination has a great relationship with the value of interlaminar stress.The interlaminar stress include one normal stress tnand two shear stresses ts，tt. In this paper，three hypotheses are made as follows：

（1）If tnis greater than or equal to zero，all the interlaminar stress will induce the occurrence of interlaminar opening failure.

（2）If tnis less than zero，the normal compressive stress tnwill put an inhibition effect on the occurrence of interlaminar shear gliding failure. And the intensity of this inhibition effect is in proportion to the value of normal compressive stress tn.

（3）The bonding layer is so thin that the damage caused by pure normal compressive stress can be neglected.

According to these hypotheses，two delamination initiation criteria were proposed.

For load cases that include normal tensile stress，delamination initiation criterion can be described as

For load cases that include normal compressive stress，delamination initiation criterion can be described as

where FI represents failure index. Superscripts “T” and“C” represent tension and compression，respectively. Subscript “DF” represents delamination failure. Moreover，，andare the effective stresses.According to Lemaitre strain equivalent principle［18］，these effective stresses can be calculated by multiplying corresponding effective strain and material’s initial stiffness. Rn，Rsand Rtare cohesive strengths. And Rnis at interlaminar normal direction，while Rsand Rtare at interlaminar tangential direction. pcnsand pcntrepresent friction coefficients which simulate the inhibition effect of the normal compressive stress.

Measuring cohesive strength is difficult，but it is relatively simple to obtain the value of interlaminar fracture strengths. Therefore，a new factor r was defined as the ratio of cohesive strengths（Rn，Rsand Rt）to interlaminar fracture strengths（Z，S31and S32）. And this factor was named as cohesive strength coefficient in present paper.

Puck［19］researched transverse compressive stress’s inhibition effect and defined two inclination parametersand. Considering the similarity between characteristics of interlaminar shear behavior and intralaminar shear behavior，in this paper，it is assumed thatequals toandequals to. For GFRP/Epoxy，= 0.25，=0.20—0.25； For CFRP/Epoxy，= 0.30，= 0.25—0.30.

In Eqs.（1），（2），the failure index FI does normally not supply quantitative information about the risk of fracture. In Puck’s theory，the stress exposure fEwas proposed to indicate the risk of fracture caused by the present loading. Using the following equation can calculate the value of fE［20］

where L and Q are the linear and quadratic terms in the failure function（Eq.（1）and Eq.（2））.

In fact，Eq.（2）depicts the intersection line ofaxis’s transverse section with delamination initiation envelope（See the red line in Fig.1）. If we calculate the stress exposure fEfor failure function（Eq.（2）），the 4th grade equation needs to be solved，which is relatively difficult. Luckily，failure functioncan also be expressed by the intersection line ofaxis’s longitudinal section with delamination initiation envelope （See the blue line in Fig.1）. Based on the above hypotheses（Eq.（2）and Eq.（3）），this longitudinal intersection line can be described by a parabolic equation，which can be seen as follows

Differentiate Eq.（4）with respect to

Then Eq.（7） can be substituted into Eq.（4）with the result

Considerations based on micro-mechanics suggest that the interlaminar fracture resistances Rsand Rtare not equal but of very similar magnitude.Thus，the elliptic function can be used to describe the relationship between parameters Rs，Rtand Rφ

Finally，by using Eq.（3）and Eq.（9），we can obtain the expression of stress exposure fEfor failure functions（Eq.（1）and Eq.（8））

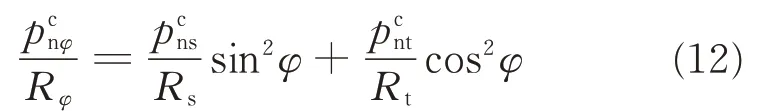
where sin2φ equals toand cos2φ equals to.

Fig.1 Envelope surface of delamination initiation

1. 2 Delamination growth criterion

After delamination initiates， the energy released during crack propagation determines the damage evolution rate. When the energy release rate reaches its critical value，the new crack surfaces will be formed. The B-K criterion［21］is a widely used delamination growth criterion. B - K criterion only involves one fitting parameter and it builds the relationship between critical energy release rate and mixed-mode ratio.

If we suppose simply that mode II fracture toughness GΙΙcequals to mode III fracture toughness GΙΙΙc，the B - K fracture criterion corresponding to mixed-mode I/II/III loading can be changed as

As mentioned above，the normal compressive stress will bring an inhibition effect on delamination.That is，this kind of inhibition effect improves the material’s interlaminar fracture toughness. Thus，the interlaminar fracture toughness can be expressed as a function of pure Mode II fracture toughness

1. 3 Cohesive zone constitutive relationship

Under the mixed - mode loading，the cohesive zone constitutive equation can be described by T - δ curve. The mathematical expression of bilinear T -δ curve can be defined as follows［1，4］

where Dijand Kijare interfacial secant stiffness matrix and interfacial initial stiffness matrix respectively.is Kronecker delta symbol and δnis interfacial normal relative displacement.

In this paper，the coupling effects between axial stresses are neglected. So all elements，except those on the principal diagonal line of matrixes Kijand Dij，equal to zero. And Kiican be determined by the definition in Ref.［1］. That is， Kiiequals to 106N/mm3（i=n，s，t）.

In Eq.（16）， dDFrepresent the interlaminar damage evolution law. And its mathematical expression can be seen as follows

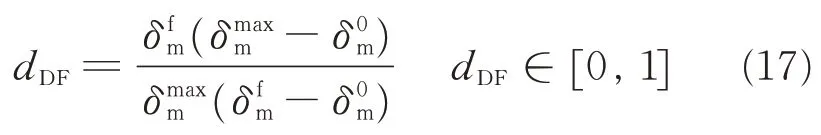
The bilinear constitutive equation corresponding to mixed-mode loading is plotted in Fig.2，where the two kinds of interlaminar load cases are discussed respectively. When the stress combination reaches point A / point C（See Fig.2），the delamination initiation will occur. And delamination keep propagating with the increasing energy release rate Gd. When Gdhas the same value of fracture toughness Gc，the new crack surfaces will be formed（See point B / point D in Fig.2）.

1. 4 Mesh size within cohesive zone

As previously mentioned，there exists an irreversible damage zone ahead of the crack tip. And the length of this zone is called cohesive zone length. For achieving an accurate numerical representation of physical cohesive zone，the mesh within cohesive zone length must be sufficiently fine to ensure that enough interface elements exist［22］.However，the excessive fine meshes will cause the increment of computational cost. So the mesh size need be well determined to keep a good balance between the analysis accuracy and computational efficiency.

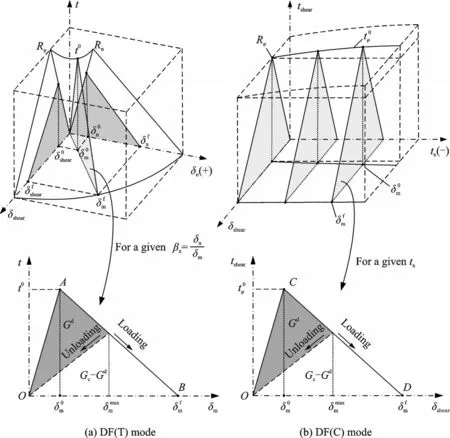
Fig.2 Bilinear constitutive description of mixed-mode delamination

Researchers have proposed many prediction models to estimate the length of cohesive zone. And these equations can be generalized as［6］

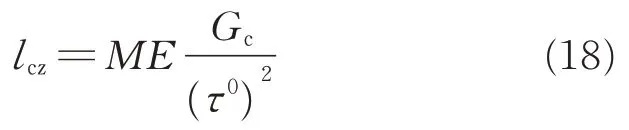
where E and Gcare material’s Young modulus and critical energy release rate，respectively. τ0is the maximum interlaminar strength，and M is a parameter that depends on the type of prediction model. M equals to 1.0 in Hillerborg model［22］，which is the most common model.

This modified cohesive zone model was implemented in commercial software ABAQUS as a userdefined mechanical material subroutine.

2 Model Verification

2. 1 Test for simulation analysis

To verify the rationality of present modified cohesive zone model，DCB，ENF，and MMB tests are simulated（See Fig.3）. The specimen is a unidirectional AS4/PEEK carbon-fiber reinforced composite. It is 102 mm long， 25.4 mm wide and 3.12 mm thick. Its material properties，pre-fabricated crack length a0and mixed - mode fracture toughness are respectively shown in Tables 1 and 2.Through adjusting the value of parameter c （See Fig. 3 and Table 2），MMB tests under different mixed - mode ratio can be conducted. Besides，the B-K parameter ζ was calculated by fitting the experimental data shown in Table 2. And the parameter ζ equals to 2.284.

The specimen’s finite element models were composed of two laminae of eight - node incompatible solid elements（C3D8I）connected together with eight-node thin cohesive elements（COH3D8）. Rigid elements were implemented to simulate the loading lever，because its stiffness is very high compared with that of the specimen. During this analysis， the displacement and the load magnitude at loading position were recorded to obtain the load -displacement curve.

Fig.3 DCB, MMB and ENF tests

Table 1 Material properties of AS4/PEEK[1]

Table 2 Dimension parameters and fracture toughness values of specimen[1]

2. 2 Influence of mesh size

Five numerical models with different element lengths（lelm）were built to simulate DCB tests. And the analysis results are shown in Fig. 4. From this picture，we can find that numerical models whose element lengths are less than 0.5 mm almost obtain the same results.（See Fig.4）.

Fig.4 Predicted load-displacement curves with different mesh sizes for DCB test

Hillerborg model［22］was used to determine the cohesive zone length of material AS4/PEEK. The calculation results is 1.53 mm. From this data，we can draw another conclusion. That is，in order to ensure the high analysis accuracy，there shall be more than two or three elements within cohesive zone length. And in this paper，the value of mesh size lelmis set as 0.5 mm to give a balanced consideration to both analysis accuracy and computational efficiency.

2. 3 Influence of cohesive strength

Several cohesive zone models with different cohesive strength ratio r were used to simulate DCB，MMB and ENF tests. Fig.5 shows the numerical results based on the same element sizes （lelm=0.5 mm）. From those curves，we find that a proper decrement of cohesive strength doesn’t greatly influence the structure’s load-displacement responses.Especially the structural initial stiffness，there are almost no influence on it. Relatively speaking，the effects of the cohesive strength become more observable when GII/GTmodal ratio increases. And the largest difference of peak loads corresponding to r=1.0 and r=0.6 is less than 6.35%，which appears in the situation of GII/GT=50%.

Fig.5 Predicted load-displacement curves of different cohesive strength ratios for DCB, MMB and ENF

2. 4 Prediction ability evaluation

The experimental data and numerical results obtained from two models（present and Camanho’s prediction［1］）are shown in Table 3 and Fig. 6. We find that structure’s initial stiffness predicted by two models are in good agreement with experimental ones. For DCB tests，two models give similar results. And compared to experimental ones，prediction errors of two models are both small. For MMB and ENF tests，the present model does a better job than Camanho’s model， due to the great effect caused by normal compressive stress. Almost all prediction errors of present model are below 10%（Only one reaches 12.85%）. Synthetically speaking， for material AS4/PEEK， let the cohesive strength coefficient r equals to 0.8 can get the best prediction results.

Table 3 The peak load data obtained from the present model and experiment(r=1.0, 0.6)

Fig.6 Comparison of the experimental data and two prediction results

3 Conclusions

Considering the promotion effect of interlaminar normal tensile stress and the inhibition effect of interlaminar normal compressive stress，two kinds of delamination initial criteria were proposed. According to the initial criteria and the theory of cohesive zone model，we proposed a modified cohesive zone model to simulate delamination failure in laminated composites. After being used to conduct the analysis of AS4/PEEK material specimens under DCB，MMB and ENF tests，this modified model is verified to be reasonable and effective.

Moreover， other three conclusions can be made as follows：

（1） The present model can do a better job than common ones when it is used to predict laminates’delamination under interlaminar compression stress.

（2）With the energy release rate unchanged，a moderate variation of cohesive strength doesn’t have great impact on the global load - displacement response.

（3） In order to keep a good balance between analysis accuracy and computational efficiency，there are shall be two or three elements within numerical cohesive zone.

Appendix

（1）Parameter δ0m

The relative displacement δmexisted between two adhesive surfaces can be expressed as

When delamination initiates，the uniaxial relative displacements at the onset of delamination can be computed by dividing the corresponding current relative displacementsδiby the stress exposure fE

Then，we can get the equation of mixed-mode relative displacement at the initiation of delamination as follows

Under the mixed - mode loading，the mixed -mode ratios of mode I，mode II，and mode III can be defined as

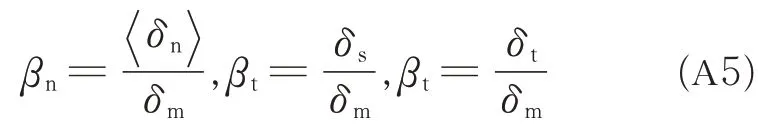
When the new crack surfaces are formed，and Gchave the same value. So energy release rate of each single-mode can be expressed as follows

Eq.（A5）can be substituted into Eq.（A6）

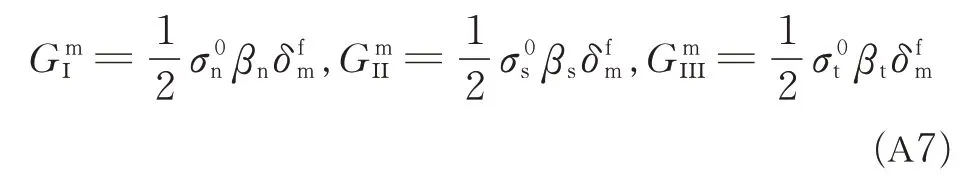
Then from Eq.（A7）and Eq.（12），the mixedmode relative displacement corresponding to total decohesion can be obtained as

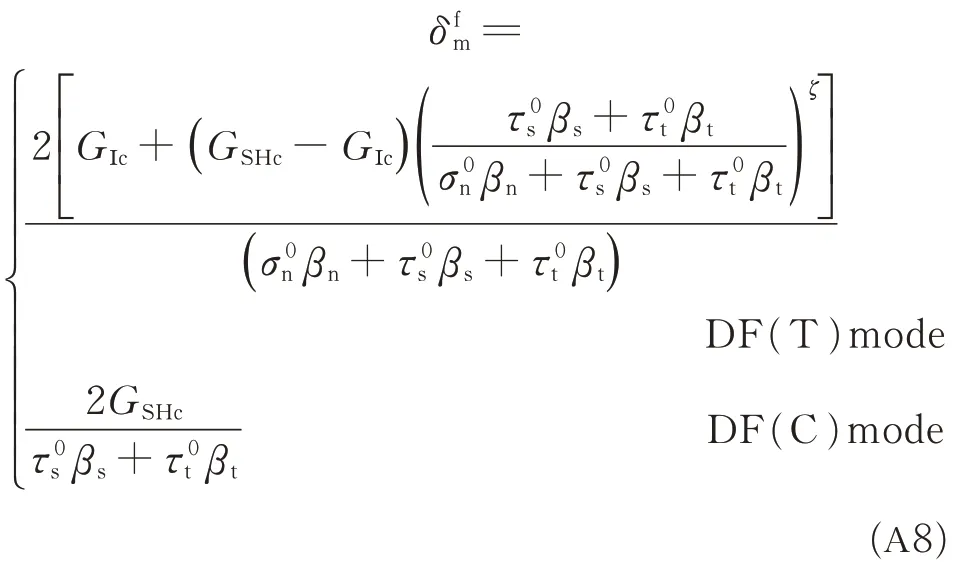
If we neglect the inhibition effects（i.e.，== 0）and make an assumption that Rs= Rtand Knn= Kss= Ktt= K，Eq.（A4） and Eq.（A8） can be simplified as Eq.（A9） and Eq.（A10）. These two equations are the same as those given in Ref.［1］where the mixed-mode ratio κ is defined as δshearδn.