基于二维涌潮数值模拟的钱塘江九溪涌潮保护方案研究
2019-12-03金建峰钱学诚张玉伦黄姿菡
金建峰,钱学诚,张玉伦,黄姿菡
(1.杭州市闲林水库管理处,浙江 杭州 311122;2.杭州市河道管理总站,浙江 杭州 310014;3.浙江省水利河口研究院,浙江 杭州 310020)
1 问题的提出
城西南排通道工程是解决杭州市城西地区内涝问题、保障城西科创大走廊防洪排涝安全的骨干工程,也是补齐杭州城市功能短板、涉及公共安全的重大民生基础设施。工程新建从五常港到钱塘江九溪段总长约13 km的深埋隧洞,衬后洞径约11 m,隧洞底高程约-50.00 m。出口新建九溪泵站,设计排涝流量200 m3/s(远期300 m3/s),并结合建设上泗沿山河挡潮闸、九溪挡潮闸等,提高之江片区和九溪十八涧排洪御潮能力(工程平面布置见图1)。前期经过多方案比选论证,拟将工程出口布置在珊瑚沙水库末端至九溪十八涧岸段。受特殊的地形条件影响,形成较为壮观的涌潮景观,但同时也是防潮的重点区域。由于工程出口涉及大型排涝泵站枢纽等水工建筑物的布置,需对该处原有堤线进行优化调整,一定程度上改变了该河段产生涌潮的地形条件。为确保工程出口建设能够满足“既保留涌潮景观,又不影响之江路交通和行人安全”的要求,研究结合工程出口的优化布置,提出3个就近保护钱塘江九溪涌潮的方案。
随着数值模拟理论与技术的不断发展与成熟,数值模拟在涌潮研究中得到越来越多的应用。近年来,国内外学者通过涌潮数值模拟在治江围涂工程、桥梁工程等涉水建筑物对涌潮影响方面的研究已取得不少成果[1-6],涌潮的数值模拟可模拟钱塘江涌潮的形成、发展和衰减的全过程,从而复演“交叉潮”“一线潮”和“回头潮”等涌潮潮景[7]。但针对钱塘江涌潮保护的研究尚不多见。本文通过建立二维涌潮数学模型,在实测水文资料验证的基础上,计算优化方案实施前后的流场及涌潮传播特性,创新性地从构筑物近区涌潮高度、涌高明显的岸线长度和涌高明显的区域面积等3个指标,对各方案的涌潮效果进行综合分析与评价。

图1 杭州城西南排通道工程平面布置示意图
2 九溪段涌潮特征
因杭州湾喇叭形平面形状使向钱塘江上游传播的东海潮波能量积聚,潮差增大,加之乍浦以上水下沙坎发育,水深急剧变浅,使潮波产生非线性畸变。形成水位骤然抬升的涨潮潮波前锋线,即为涌潮[8]。钱塘江九溪段位于九溪弯道的凹岸,由于急弯和珊瑚沙水库围堤与之江路海堤围成的局部喇叭形平面形态,加之九溪顺坝的共同作用,在秋季大潮期,沿山河排涝闸前水域能形成较为壮观的回头潮景观。根据现场调查九溪岸段的涌潮演变发展过程通常表现为:涌潮在到达九溪顺坝及岙口前,形态比较规则一致,涌潮潮头线主体呈现略向前凸的弧形,由东北向西南推进;近岸区水深较浅,潮头破碎;主槽区水深加深,涌潮呈现波状,甚至消失;到达九溪顺坝后,潮头翻越顺坝,撞击海塘,在海塘坡脚进一步涌高并向九溪岙口推进,撞击凹口终点 — 沿山河水闸,激起巨浪,高者可达10余米,之后潮头被反射,沿海塘塘脚向后折返,如浪头超过海塘塘顶,则潮水涌到之江路上。钱塘江九溪段航拍见图2。

图2 钱塘江九溪段航拍图
3 涌潮的保护方案
本文在满足工程布置基本需求的前提下,基于九溪岸段涌潮景观保护及减小涌潮危害等因素,通过对工程出口进行优化布置,提出3个涌潮保护方案。
方案1的岸线及工程布置见图3。该方案将沿山河闸紧贴珊瑚沙水库并往岸边调整,闸泵轴线平行布置。沿山河新闸将在新堤线基础上后退约110 m,开口宽约210 m,以减小对涌潮影响。

图3 钱塘江九溪岸段涌潮保护方案1图
方案2的岸线及工程布置见图4。该方案将沿山河闸在新堤线基础上略往后约66 m,开口宽度与闸宽相同,闸泵轴线平行布置。为减小工程对涌潮影响,方案2还进一步在九溪排涝闸下游的三角区域内形成人工喇叭口状岸线形态,以提升涌潮效果。该喇叭口开口宽约230 m,平均深度140 m。
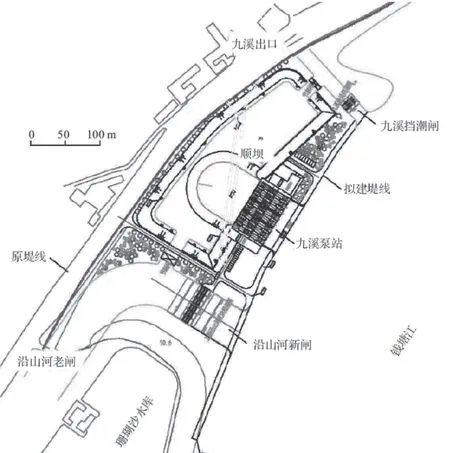
图4 钱塘江九溪岸段涌潮保护方案2图
方案3的岸线及工程布置见图5。该方案将泵站及隧洞出口一起向北移,为维持涌潮尽最大限度让出通道,沿山河新闸在新堤线的基础上后退约210 m,开口宽约190 m。调压池面积不足部分通过下游三角带围出1个水池连通前池,共同调蓄。
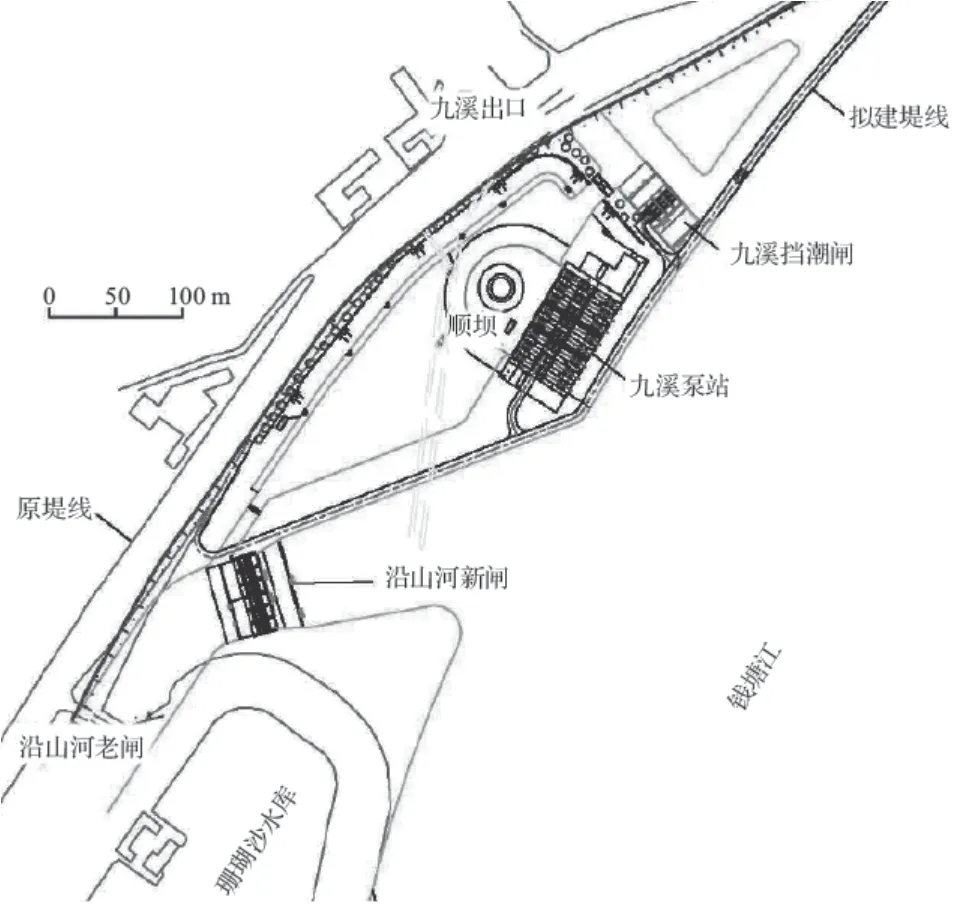
图5 钱塘江九溪岸段涌潮保护方案3图
4 九溪涌潮数学模型的计算
4.1 数学模型简介
构建涌潮数学模型的基础是求解基于有限体积法离散的非恒定二维浅水流动方程,其核心是法向数值通量的计算以及底坡源项的处理。因法向数值通量求解方法不同,发展了许多能模拟浅水间断流动的计算方法,如Godunov型格式、TVD格式、MacCormack格式、BGK格式等。因KFVS格式具有计算稳定、模拟精度高、守恒性好、边界和地形拟合能力强等优点[9]。因此,本文基于Boltzmann方程、KFVS格式建立平面二维涌潮数学模型,在对实测水文资料验证的基础上,对九溪岸段现状涌潮与3个优化后方案的涌潮效果进行数值计算分析。
非恒定二维浅水流动方程守恒形式为:

式中:
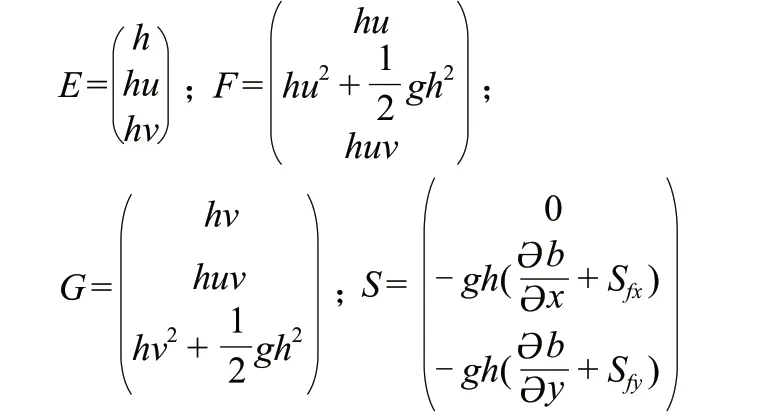
式中:u、v分别为x、y方向的流速分量,m3/s;h为水深,m;g为重力加速度,m/s2;b为河床高程,m;Sfx、Sfy分别为x、y方向的阻力项。
计算域采用任意三角形剖分,并采用网格中心格式,即将物理量定义在三角形形心,控制体即为单元本身。设Ωi为第i个三角形单元域,Гi为其边界,对式(1)应用有限体积法离散,并利用格林公式,则有:
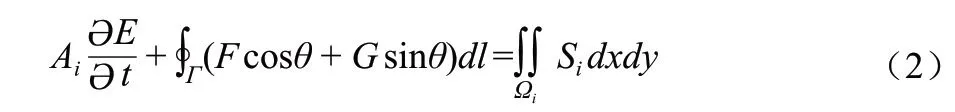
式 中:Ai为 三 角 形 单 元Ωi的 面 积,m2;(cosθ,sinθ)为Г外法向单位向量;dl为线积分微元,m。对式(2)时间导数采用前差,记Fn=Fcosθ+Gsinθ,即得基本数值解公式为:
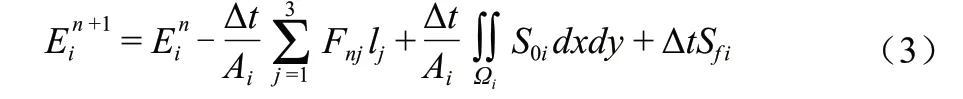
式中:Δt为时间步长,s;下标j表示i单元第j边;lj为三角形边长,m;上标n为时间步;S0i为底坡源项;Sf i为阻力项。
求解守恒型非平底浅水流动方程时,需对底坡源项作特殊的处理,以致方程左端的压力项与方程右端的底坡源项在每个单元内“和谐”。建立和谐格式的关键是底坡源项的离散与压力项相同,这里不再详述。另外,为提高计算精度,可应用与MUSCL类似的方法,将空间一阶精度格式扩展到空间二阶精度。
上述模型已经静水、斜激波等典型算例检验。
4.2 模型概化
本次数学模型研究范围上游边界选在富春江电站,下边界选在澉浦,结合涌潮特征计算需要,对闻家堰至七堡河段网格进行局部加密处理,最小网格尺度2 m。模型计算范围及网格布置见图6。
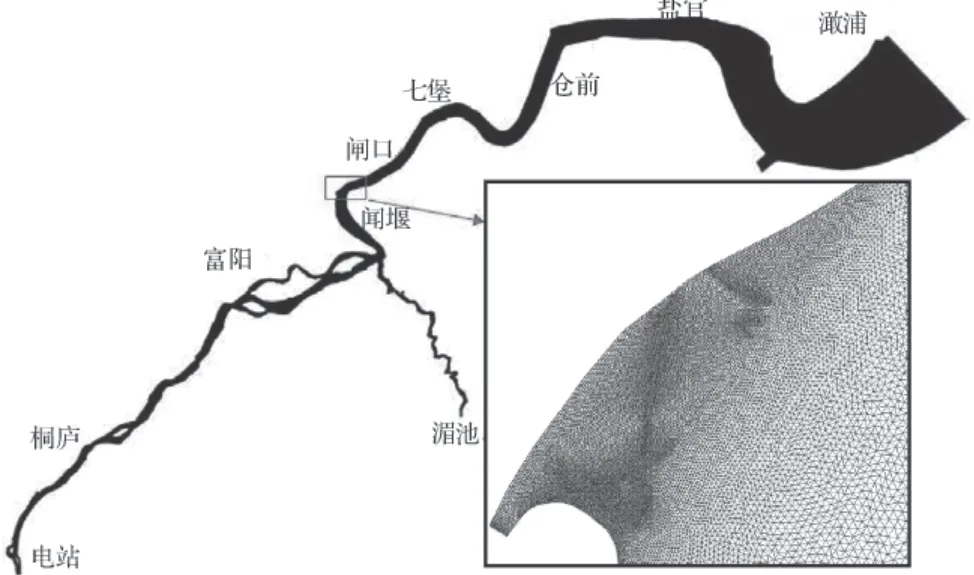
图6 涌潮数学模型计算范围及网格布置示意图
4.3 模型验证
模型验证了2018年6月闸口、闻堰、富阳和九溪等4个沿程水位站的潮位资料以及工程河段5个水文测点(测点布置见图7)的实测流速过程,验证时计算地形采用与实测水文资料同步的地形资料。潮位验证结果见图8,由图8可见,各站点潮位过程高低潮位值、潮差和相位计算与实测均吻合较好。经统计,潮位验证中96.2%的高低潮位值点据误差在0.10 m以内(其中高潮位最大误差为0.37 m,低潮位最大误差0.10 m)。潮流验证见图9 ~ 10,可见流速过程验证吻合较好,特别是结果中各站点涨急流速、落急流速均能捕捉,涨、落急流速验证中92.5%的点据误差在20.0%以内。
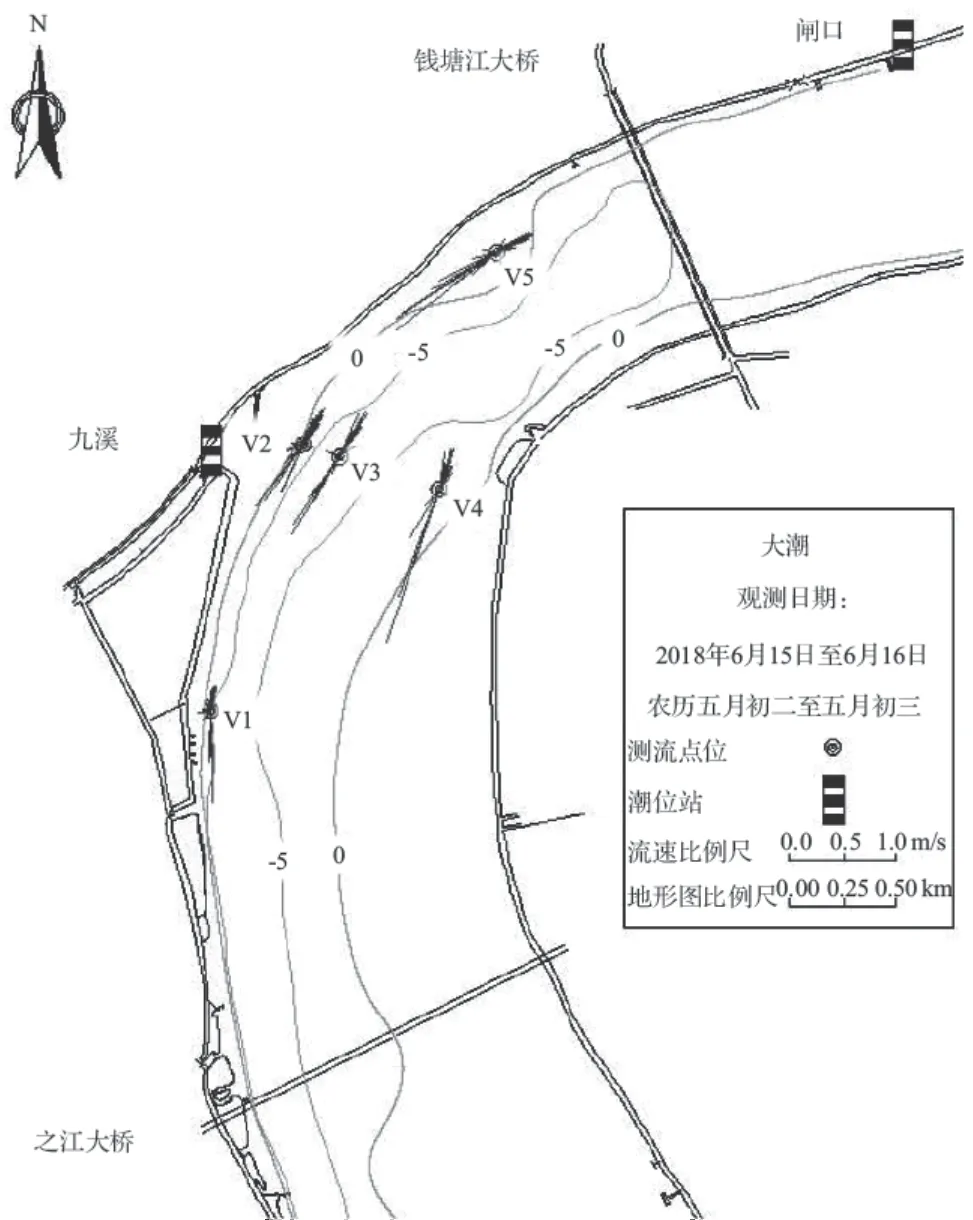
图7 钱塘江九溪段水文测点布置示意图
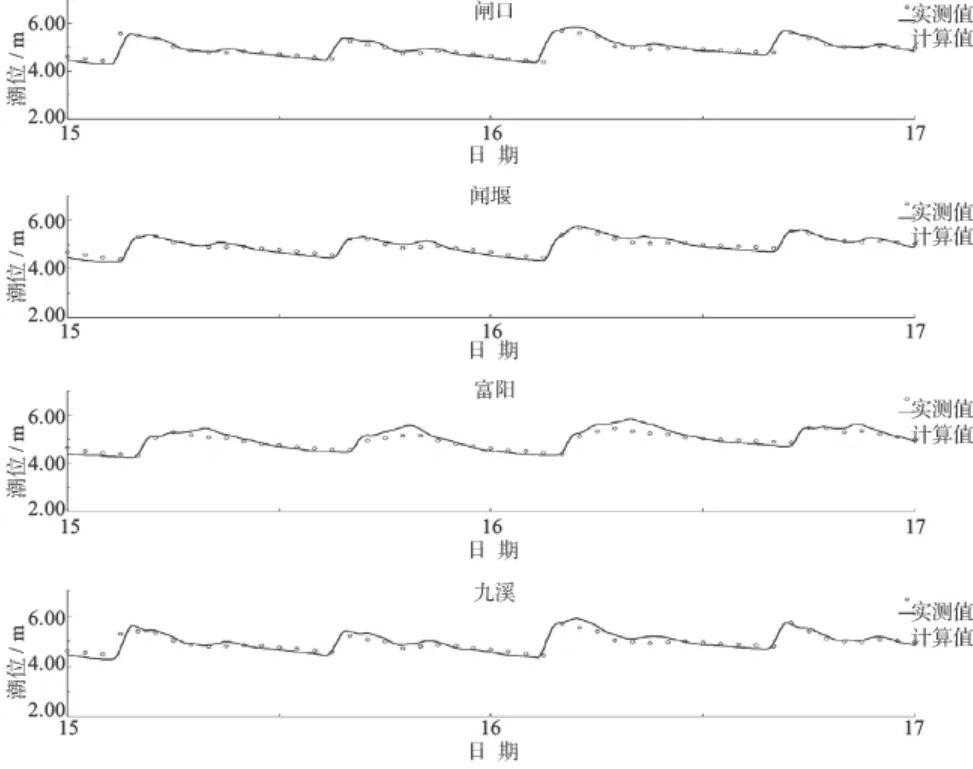
图8 2018年6月测次潮位验证图
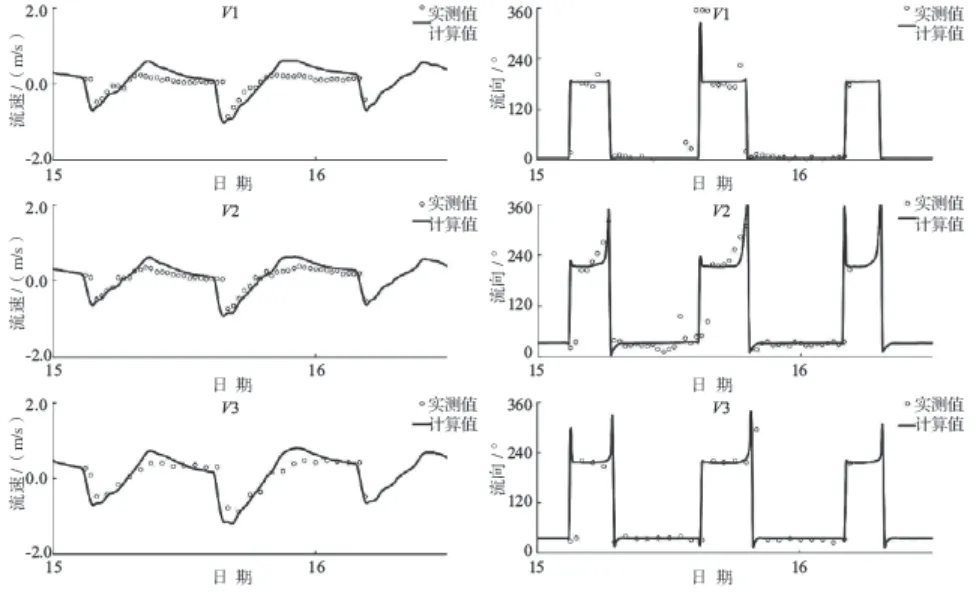
图9 2018年6月测次V1 ~ V3测点潮流流速、流向验证图
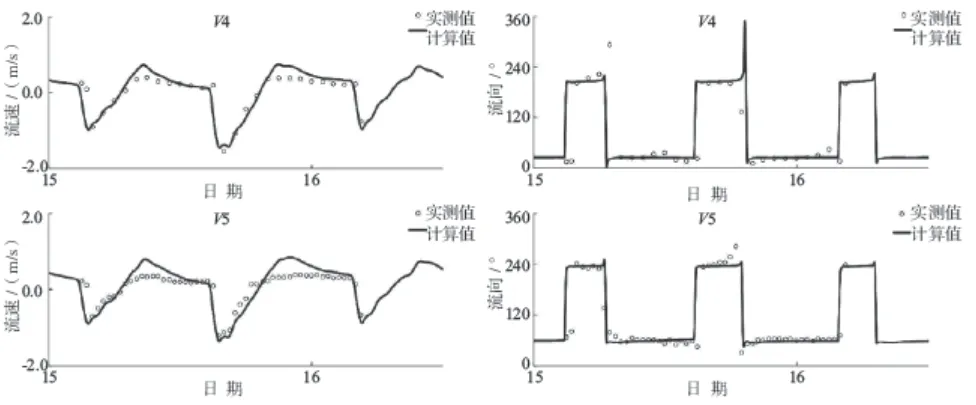
图10 2018年6月测次V4、V5潮流流速、流向验证图
4.4 计算条件及工况组次
为分析九溪岸段优化对钱塘江沿程各观潮点涌潮特征的影响,计算上游流量边界选择富春江电站多年平均径流流量,下游潮位边界选择典型秋季大潮过程,模型地形选择最新实测地形资料。根据前期研究,影响钱塘江涌潮强弱的最重要因素可归纳为潮汐、山水和江道地形等因素。对江道地形,计算水文条件选用钱塘江河口治理基本到位后、江道容积偏大的年份,取当年潮差保证率接近1%(2.60 m)和20%大潮(1.77 m,本次水文测验期间实测大潮接近该值)。由此,九溪岸段优化涌潮影响数学模型计算涉及的计算组次主要有现状工况以及3个优化方案等4种工况、前述2种水文条件组合而成的8组次(见表1)。
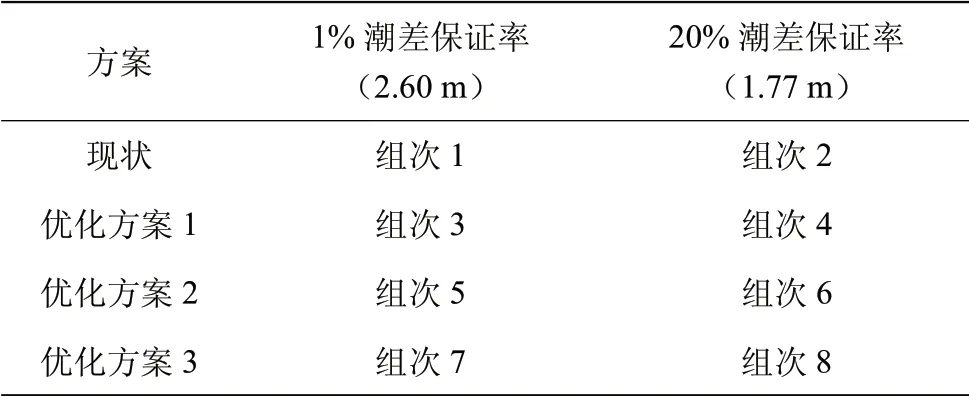
表1 工况组次表
4.5 涌潮影响评判比较指标
由于每个工程方案占用沿山河排涝闸下游约0.5 ~ 1.0 km岸段前沿的钱塘江水域,新方案形成的涌潮观赏区域和观赏形态发生较大的转移和变化。为综合评价涌潮的观赏性,将涌潮观赏性分解为3部分:构筑物近区涌潮高度、掀起涌浪幅度明显的岸线长度和涌高明显的区域面积等3个指标。将近区涌潮高度指标权重设为0.4,岸线长度和区域面积权重均设为0.3,假定现状涌潮综合系数为1.0。各方案综合系数计算方法=方案实施后的各项指标值/现状的对应指标值×指标权重的合计值。由于平面二维涌潮模型的局限性,目前尚无法模拟涌潮撞击建筑物后贴壁有限量水体冲天而起形成水花的这一过程,本文涌高主要是指近岸区大部分水体的平均涌潮涌高幅度。
4.6 计算结果
图11为1%潮差保证率下,不同方案工程区域涌潮高度平面分布图。由图11可知,由于九溪岸段优化大幅改变了该区域岸线形态,因此九溪岸段前沿水域涌潮高度分布也随之发生较大改变。现状涌潮通过九溪顺坝和口门进入岙口,撞击沿山河闸,涌高明显的主要有3个区域:沿山河闸前、顺坝与海塘交叉口内侧和外侧。顺坝外侧、靠近江道主槽侧涌潮高度一般在0.70 ~ 0.80 m,沿山河闸前沿涌高1.49 m。优化方案1实施后在新堤线外侧涌潮高度一般在0.70 ~ 0.80 m,沿山河新闸和九溪新闸由于局部内凹,对涌潮有集聚发展作用,涌高幅度上升至0.90 m左右。优化方案2也有类似规律,在下游三角区区域内形成人工的喇叭口状岸线形态,涌潮在此集聚发展,近岸侧涌高1.45 m。优化方案3在沿山河排涝闸内涌潮聚集效果也较为明显,近岸侧涌高1.11 m。20%潮差保证率下工程对涌潮的影响特征类似,不再赘述[10]。
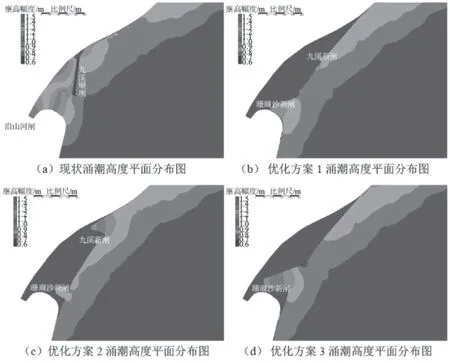
图11 九溪岸段现状及各优化方案涌潮高度平面分布(1%潮差保证率)图
为了更全面地反映工程对岸段前沿涌潮强度、形态及观赏性的影响。分别采用1%、20%潮差保证率条件下岸段前沿明显区别于相邻区域的0.90,0.70 m涌高值,分别统计分析各组次过程中曾出现大于相应涌高值的岸线长度和面积,将有关统计结果一并列于表2和表3。

表2 各方案涌潮计算成果(1%潮差保证率)表

表3 各方案涌潮计算成果(20%潮差保证率)表
计算结果表明,工程建设对涌潮形态、高度及观赏性存在一定影响。与现状相比,优化方案1中的涌潮高度减小明显,涌高明显大于周边水域的岸线长度和包络面积均最小,观赏价值较低;优化方案2涌潮高度与现状接近,涌高明显大于周边水域的岸线长度和包络面积约为现状的1/3,但总体观赏效果达到现状60%以上;优化方案3与方案2涌高及观赏性较为接近,但涌潮高度略小于方案2,涌高明显大于周边水域的岸线长度和包络面积均稍大于方案2,观赏性相当。但从喇叭口岸线形态、出口排涝泵闸工程的布置与运行安全来看,方案2更优。
5 结 语
(1)城西南排通道工程规划出口布置需对钱塘江九溪段原有堤线进行调整,一定程度上改变了产生九溪涌潮的地形条件。为保护涌潮资源,研究结合工程出口的优化布置,提出3个就近保护涌潮的方案,并基于Boltzmann方程、KFVS格式建立平面二维涌潮数学模型对各方案的涌潮效果加以分析验证。
(2)涌潮数学模型计算分析的结果表明,工程建设对涌潮形态、高度及观赏性存在一定的影响。与现状相比,3个优化方案中,方案1的涌潮观赏价值最低,方案2与方案3涌高及观赏性接近,但方案2兼具涌潮形成的喇叭口岸线形态、河床逐步抬升、涌潮正面迎击等多个有利因素,有利于相关排涝泵闸工程的布置与运行安全,可重点作为后续进一步优化的方案。
(3)初设阶段在优化方案2的基础上,可进一步围绕涌潮保护细部设计工作开展相关岸段景观设计,同时结合大比尺物理模型试验与三维涌潮数学模型计算,对涌潮效果做更进一步优化。
