超细粉体静电场湿法分级过程数值模拟

郑向阳 俞建峰 刘志强 俞俊楠 李志华 黄然 金楠 宋明淦

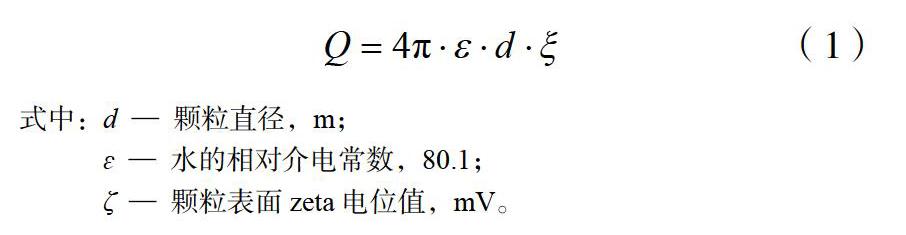
摘      要：基于计算流体动力学的离散相模型和RNG k-ε湍流模型，将流场与电场耦合，对超细粉体静电场湿法分级过程进行数值模拟。结果表明：分级区内流体的竖直方向分速度为零，流体仅做水平流动，该区域电场强度分布较为均匀，可视为匀强电场区域;进料速比和进料流速都是通过影响水平流速间接影响分级效果，水平流速越小，颗粒部分分级效率越大，分级粒径越小;增加电极电压，可提高部分分级效率，减小分级粒径。

关  键  词：静电场;湿法分级;数值模拟;部分分级效率

中图分类号：TQ 028.8       文献标识码： A       文章编号： 1671-0460（2019）10-2428-05

Abstract： By coupling the flow field with the electrostatic field， the wet classification process of ultrafine powder in electrostatic field was simulated numerically with computational fluid dynamics， in which the discrete phase fluid model and RNG k-ε turbulence model were applied. The results showed that the vertical velocity of the fluid in the classification zone was zero， the fluid only flowed horizontally， and the electric field intensity distribution in this region was relatively uniform， so it was regarded as a uniform electric field. Both the feed rate ratio and the feed flow rate indirectly affected the classification effect by affecting the horizontal flow rate. The smaller the horizontal flow rate， the higher the partial classification efficiency， and the smaller the classification particle size. Increasing the electrode voltage can improve the partial classification efficiency and reduce the classification particle size.

Key words： Electrostatic field; Wet classification; Numerical simulation; Partial classification efficiency

超細粉体因具有高比表面积、高表面能和高活性，在催化、光电、磁性、力学等方面表现出独特的优异性能，被广泛应用于国防工业、磁记录设备、计算机工程等领域[1]。为满足不同领域对超细粉体粒径大小和粒度分布的严格要求，需要采用分级技术对其进行分级处理。通常粉体分级可以采用干法分级和湿法分级，其中湿法分级更易于提高超细粉体的分散性，同时边界效应影响较小、分级过程相对容易控制[2，3]。然而，常用的重力沉降分级、溢流分级和离心分级等方法难以获得稳定、均匀、强大的分级力场，导致产物分级锐度低、粒度分布宽，严重影响其应用效果[4]。基于颗粒表面荷电特性的静电场分级技术备受研究者关注，已有学者对此展开了相关研究。国内学者对静电场分级技术的研究主要集中在静电场干法分级领域[5-7]，对应用静电技术进行超细粉体湿法分级的研究则比较少。然而，静电场干法分级需要在数十千伏的高电压下对粉体颗粒进行充分荷电，能耗高且存在较大安全隐患。

在静电场湿法分级方面，国内仅有南京理工大学学者李凤生[8]、裴重华[9]等人进行过相关研究，并采用自制的装置对超细黑索金颗粒进行分级实验，原物料平均粒径为5.53 μm，分级后得到平均粒径为2.03 μm的产品。近年来，日本广岛大学学者在静电场湿法分级方面取得了新的研究进展，先后设计了静电水力旋流器[10，11]、静电水淘析器[12]和静电沉降水筛[13]等装置，对静电场湿法分级开展了相关实验研究，将分级粒径控制在亚微米级范围。

为进一步探究超细粉体静电场湿法分级的分级特性，本文应用COMSOL 5.3a多物理场耦合分析软件，对超细粉体静电场湿法分级过程进行数值模拟，研究装置内部的流场和电场的分布规律，考察进料速比、进料流速及电极电压等因素对分级效果的影响规律，以期为超细粉体静电场湿法分级技术研究和装置开发提供借鉴。

1  几何模型和网格划分

装置结构如图1所示，其内缘尺寸为：长×宽×高=480 mm×80 mm×110 mm;进料口、进水口、溢流口及底流口尺寸相同，均为：长×宽=80 mm×10 mm;两电极板间距为100 mm，长度为400 mm;层流板均匀分布，厚度为2 mm，数量为10，间距为7 mm。在水平方向上将分级装置分为进料区（0

由于流体在z方向不存在力场作用，可忽略z方向流动效应，将装置简化为二维模型进行数值模拟。采用四边形网格对流体域进行网格划分，无滑移壁面采用边界层网格处理，得到分级装置模型网格划分结果如图2所示，网格数量为20 943，平均网格单元质量为0.9 676。

2  计算条件设置

2.1  物理场条件

进料口和进水口为速度入口，属于研究变量。溢流口和底流口为压力出口，相对压力值为0，即为自由出流状态。无滑移壁面采用壁函数处理。液相为水，密度为103 kg/m3，动力粘度为1.01×10-3 Pa?s，电导率为5.5×10-6 S/m，相对介电常数为80.1，流体受重力场作用，重力加速度为g=9.8 m/s2。

固体颗粒在中性液体中通常呈现电负性[14，15]，为了增大颗粒沉降力场，电场强度方向应竖直向上。设置上电极板电位条件为接地，下电极板电势为正值，二者之差为电极电压，属于研究变量。

2.2  粒子属性

由于离子溶解、基团电离、晶格取代等作用，与水等极性液体介质接触的绝大多数固体颗粒表面会呈现一定电性，当颗粒相对于流体介质运动时，颗粒表面电位即为zeta电位[16]。假设颗粒为球形，在粒子半径较小的稀溶液中，颗粒表面电荷量与zeta电位具有正比例关系，即：

设置粒子从进料口释放，初始速度与进料口液体流速相同，释放1、2、3、4、5、6、7、8、9和10 μm共计十种粒径的粒子，释放方式为一次性释放，每种粒子数量均为1 000，密度为2.3×103 kg/m3，取zeta电位为-10 mV，按式（1）计算荷电量。设置壁面条件为反弹，溢流口和底流口条件为冻结，采用粒子计数功能统计到达溢流口和底流口的颗粒数量。颗粒主要受到流体曳力、电场力和重力的作用，在流体流动粒子追踪模块将曳力与流场耦合、将电场力与静电场耦合，并添加重力属性。

2.3  求解设置

本文采用离散型模型，仅考虑连续相流体对离散相颗粒的影响即单向耦合，忽略颗粒与颗粒之间、颗粒对流体的作用以及荷电颗粒产生的微弱空间电场。数值模拟采用分布求解方式进行，即首先进行稳态计算，得到稳定的多物理场，然后添加离散项颗粒，进行分级过程的瞬态模拟，计算到达溢流口和底流口的颗粒数量。

3  模拟结果及分析

部分分级效率是指到达底流口的某直径颗粒总质量与原料中该粒径颗粒总质量之比，数值模拟时统计颗粒数量并采用式（2）进行计算：

3.1  进料速比的影响

在进料流速为0.4 mm/s，电极电压为100 V条件下，选择进料速比（进料流速：进水流速）为1∶2、1∶3、1∶4、1∶5和1∶6五种条件，考察进料流速对分级效果的影响。图3为不同进料速比的速度分布，图4为分级效率。

如图3，由于进水口、溢流口及底流口在竖直方向上，故进料区和收集区的流体水平方向分速度小而竖直方向分速度大。由图3（a），不同高度处的流体水平方向流速最终将相等，且进料速比越小，达到稳定速度时所需水平距离越长。这是因为，进料速比越小，进料口与进水口速度相差越大，达到稳定速度所需时間越长，距离越大。由图3（b），分级区内流体竖直方向分速度几乎为零，且与进料速比无关。

如图4所示，进料速度一定时，进料速比的比值越大，部分分级效率越大，分级粒径越小。结合图3可知，进料速比越大，水平方向流速越小，颗粒在分级装置内停留时间越长，达到收集区时颗粒竖直方向沉降距离增大，分级效果越好。

3.2  进料流速的影响

在进料速比为1∶4、电极电压为100 V条件下，选择进料流速为0.2、0.3、0.4、0.5和0.6 mm/s五种条件，考察进料流速对分级效果的影响。图5为不同进料流速的速度分布，图6为分级效率。

如图5（a）所示，进料流速越大，最终稳定速度越大，达到稳定速度时所需水平距离越长。这是因为，进料速比一定时，进料流速越大，进料口和进水口进入的流体水平方向流速越大，达到稳定时水平方向位移越大。由图5（b），不同进料流速下，分级区内流体竖直方向分速度也为零。结合图3（b）可知，分级区内流体作水平流动，与进料流速和进料速比均无关，即分级区内颗粒在竖直方向的沉降运动与流体流动无关。

如图6所示，进料流速越大，分级粒径越大，这是由于进料流速增大，颗粒水平方向速度增大，竖直方向沉降时间减少，导致分级效率减小。这意味着，通过减小进料流速，在一定程度上可以提高部分分级效率，减小分级粒径。

3.3  电极电压的影响

在进料速比为1∶4、进料流速为0.4 mm/s条件下，选择电极电压为0、50、100和150 V四种条件，考察电极电压对分级效果的影响。图7为分级装置内部电场强度分布，图8为不同电极电压的分级效率。

如图7（a），电场强度沿水平方向变化较大。在电极板左右端面附近区域，由于电压值突变，电场强度变化较大，在80

如图8所示，电极电压越大，部分分级效率越大，分级粒径越小。这是因为，电极电压越大，电场强度就越大，颗粒沉降受力越大，其沉降速度和沉降速度差也就越大，故而部分分级效率增大，分级粒径减小。由图8可知，施加150 V电压，可将分级粒径减小至约2.8 μm。

4  结 论

对超细粉体静电场湿法分级过程进行了数值模拟研究，为超细粉体静电场湿法分级技术研究和装置开发提供了参考依据。在本研究的条件范围内，得出如下结论：

（1）分级区内流体做水平流动，颗粒的沉降动力来源为重力和电场力。进料速比和进料流速均通过影响颗粒水平方向流速来影响分级效果。流速越大，颗粒在分级装置内停留时间越短，沉降距离越小，部分分级效率越低。

（2）分级区内可看作是匀强电场区域，通过改变电压，可以在分级装置内部形成较为理想分级力场。其他条件一定时，电极电压越高，颗粒的部分分级效率越大，分级粒径越小。通过施加电压，可以在保证分级速度的前提下提高部分分级效率。

参考文献：

[1] 王俏，齐红军. 超微细粉体材料前景广阔[J]. 当代化工，2002（02） ：98-100.

[2] 王红军. 多层陶瓷电容器用超细镍粉的分散与分级行为研究[D]. 长沙：中南大学，2007.

[3] 周子然，杨刚，葛晓陵，等. 微纳稀土颗粒精密分级实验及理论研究[J]. 中国稀土学报，2014，32（4）：501-506.

[4] 邓丽荣，王晓刚，王丹，等. 超微粉体上升层流水力分级实验研究[J]. 中国粉体技术，2014，20（2） ：22-24.

[5] 徐政，谢涛，卢寿慈，等. 粉体的静电分级[J]. 过程工程学报，2007，7（1）：105-109.

[6] 刘建平，王成端. 超细粉体静电切向分级研究[J]. 中国粉体技术，2003，9（2）：32-33.

[7] 张吉光，李华，王道连，等. 静电旋风分离器流场的实验研究[J]. 流体机械，2002，30（10）：4-7.

[8] 李凤生，白华萍，张兴明，等. 超细粉体湿法分级技术研究[J]. 化工进展，1997（6）：16-19.

[9] 裴重华. 超细粉体静电场湿法分级原理研究[D]. 南京：南京理工大学，1996.

[10]Nenu R K T，Yoshida H，Fukui K，et al. Separation performance of sub-micron silica particles by electrical hydrocyclone[J]. Powder Technology，2009，196（2）：147-155.

[11]Yoshida H，Hayase Y，Fukui K，et al. Effect of conical length on separation performance of sub-micron particles by electrical hydro-cyclone[J]. Powder Technology，2012，219：29-36.

[12]Yoshida H，Fukui K，Yamamoto T，et al. Continuous Fine Particle Classification by Water-Elutriator with Applied Electro-potential[J]. Advanced Powder Technology，2009，20（4）：398-405.

[13]Shirasawa N，Matsuzawa M，Fukazawa T，et al. Fine particle classification by a vertical type electrical water-sieve with various particle dispersion methods[J]. Separation & Purification Technology，2017，175：107-114.

[14] 蔡颖莹，肖香珍. 单分散SiO₂胶体粒子的Zeta电位研究[J]. 河南机电高等专科学校学报，2015（2）：24-27.

[15] Barisik M，Atalay S，Beskok A，et al. Size Dependent Surface Charge Properties of Silica Nanoparticles[J]. Journal of Physical Chemistry C，2014，118（4）：1836-1842.

[16]劉洪国，孙德军，郝京诚. 新编胶体与界面化学[M]. 北京：化学工业出版社，2016：209-218.