2019年高考数学模拟试卷（三）

2019-12-02本刊编辑部试题研究中心

中学生数理化·高三版 2019年8期

关键词：过点车速中点

本刊编辑部试题研究中心

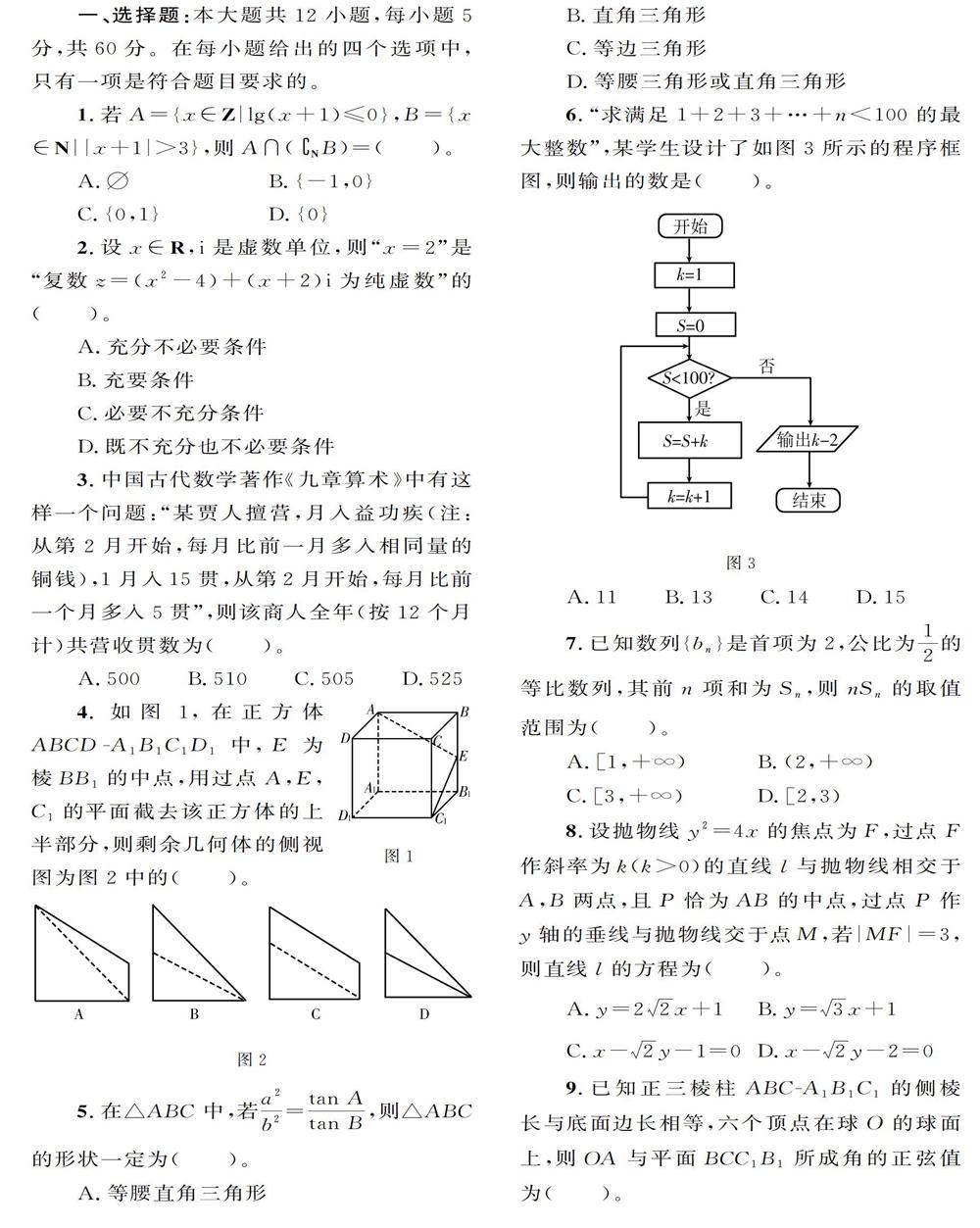
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

3.中国古代数学著作《九章算术》中有这样一个问题：“某贾人擅营，月人益功疾（注：从第2月开始，每月比前一月多人相同量的铜钱），1月人15贯，从第2月开始，每月比前一个月多人5贯”，则该商人全年（按12个月计）共营收贯数为（）。

A.500

B.510

C.505

D.525

4.如图1，在正方体ABCD -AiBlCiDi中，E为棱BBi的中点，用过点A，E，Cl的平面截去该正方体的上半部分，则剩余几何体的侧视图为图2中的（）。

6.“求满足l+2+3+-+n<100的最大整数”，某学生设计了如图3所示的程序框图，则输出的数是（）。

A.11

B.13

C.14

D.15

7.已知数列{bn）是首项为2，公比为1/2的等比数列，其前”项和为Sn，则nSn的取值范围为（）。

A.[1，+∞）

B.（2，+∞）

C.[3，+∞）

D.[2，3）

8.设抛物线y2=4a-的焦点为F，过点F作斜率為k（k>0）的直线Z与抛物线相交于A，B两点，且P恰为AB的中点，过点P作y轴的垂线与抛物线交于点M，若IMFl =3，则直线l的方程为（）。

A.y =2√2x+l B.y=√3x+l

C.x-√y-1=0 D.x-.2y 2=0

9.已知正三棱柱ABC-AiBlCi的侧棱长与底面边长相等，六个顶点在球O的球面上，则OA与平面BCClB1所成角的正弦值为（）。

18.（本小题满分12分）

为了研究家用轿车在高速公路上的车速情况，交通部门对100名家用轿车驾驶员进行调查，得到其在高速公路上行驶时的平均车速情况为：在55名男性驾驶员中，平均车速超过100 km/h的有40人，不超过100 km/h的有15人;在45名女性驾驶员中，平均车速超过100 km/h的有20人，不超过100 km/h的有25人。

（1）完成表l所示的列联表，并判断是否有99.50/的把握认为平均车速超过100 km/h的人与性别有关。速公路上行驶的大量家用轿车中随机抽取3辆，记这3辆车中驾驶员为男性且车速超过100km/h的车辆数为X，若每次抽取的结果是相互独立的，求X的分布列和数学期望。

参考数据（表2）与公式：

19.（本小题满分12分）

如图5，已知多面体PABCDE的底面ABCD是边长为2的菱形，PA上底面ABCD，ED∥PA，且PA =2ED =2。

（l）证明：平面PAC⊥平面PCE;

（2）若直线PC与平面ABCD所成角为45°，求二面角P-CE-D的正弦值。

20.（本小题满分12分）

已知M（ √2，o）为一定点，P是圆N：x2+y2- 2√2x- 14=0上的动点，PM的垂直平分线交PN于点Q。

（l）求点Q的轨迹方程;

（2）过点A（-2，0）作斜率为k（k≠0）的直线l交点Q的轨迹于点B，交y轴于点C。已知D为AB的中点，证明：存在定点E，对于任意的k（k≠0）都有OD⊥CE。

21.（本小题满分12分）

（二）选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。答题时请写清题号并将相应信息点涂黑。