迈克耳孙干涉仪应用功能拓展研究

袁婷

摘要：在保证迈克耳孙干涉仪原有结构和功能不变的前提下，加装了部分辅助器件，实现了迈克耳孙干涉仪应用功能的拓展，扩充了实验教学内容，激发了学生的学习兴趣和创新意识。

Abstract： On the premise that the original structure and function of the Michelson interferometer remain unchanged， some auxiliary devices are installed to expand the application function of the Michelson interferometer， expanding the content of experiment teaching and stimulating students' learning interest and innovative consciousness.

关键词：迈克耳孙干涉仪;应用拓展

Key words： Michelson interferometer;application expansion

中图分类号：O436.1                                      文献标识码：A                                  文章编号：1006-4311（2019）30-0183-03

0  引言

迈克尔孙干涉仪，是1881年美国物理学家迈克尔孙和莫雷合作，为研究“以太”漂移而设计制造出来的一种精密光学仪器。它是许多近代干涉仪的原型，是传统的经典光学仪器之一。目前大学物理实验中“迈克耳孙干涉仪”的实验内容，主要是测量激光波长，观察光的等倾干涉和等厚干涉现象，实验内容较为单一。我们在保证迈克耳孙干涉仪原有结构和功能不变的前提下，加装了部分辅助器件，对迈克耳孙干涉仪的应用功能进行了拓展。

迈克尔孙干涉仪的光路见图1，G1、G2分别是分光板和补偿板。光在分光板被分成反射光束1和透射光束2，两束光的振幅（光强）基本相等。M1和M2为两个互相垂直的平面反射镜，镜面与G1成45°角。1、2两束光经M1、M2反射后在E区相遇，产生干涉。补偿板G2完美补偿了分光板G1所带来的光程差。

为了研究迈克尔孙干涉仪所形成的干涉现象，可作一虚平面M'2，它是平面镜M2通过分光板G1形成的虚像，其位置在M1附近。当观察者在E区朝G1方向观察时，光束2好像是从M'2入射过来。因此，两束光在E区产生的干涉可以看成是由平面镜M1与M'2所反射的相干光形成的。

1  透明材料厚度和折射率的测量

1.1 实验原理

用迈克尔孙干涉仪测量透明材料的厚度和折射率，一般采用白光光源，通过观察彩色条纹的方法来测量。其基本原理是：不放入待测材料时，调出白光干涉彩色条纹，即调节光路1与光路2等光程，然后将待测材料插入光路1并与M1平行放置，此时由于光路1光程的变化，彩色条纹消失。通过M1移动反射镜，直至再次调出彩色条纹，通过的移动距离得到材料的厚度和折射率。然而，上述方法具有一定的局限性：①白光相干长度较小，调出彩色条纹的難度较大;②得到的是混合光的折射率，无法得到单色光的折射率。

我们采用单色光来进行实验，首先，在光路中不放入待测材料，调出等倾干涉圆环，并移动M1找到圆环吞入和吐出的临界点，即光路1和光路2等光程、M1与M'2重合的位置，然后将待测材料平行于M1放入光路1中。由于材料的插入，光路1的光程将发生改变，此时我们向内移动M1，若M1移动的距离为l，材料厚度为t，如图2所示，则插入材料后引起的光程差为：

（1）

产生干涉亮条纹的条件为：

（2）

利用折射定律，三角函数公式以及泰勒级数展开式，并忽略一些极小项，（2）式可化简为：

（3）

（3）式取微分得：

（4）

则：        （5）

由（5）式可知，当■>0时， 若l增加，条纹向外吐出，l减小，条纹向内吞入;当■<0时，若l增加，条纹向内吞入，l减小，条纹向外吐出。条纹吞入和吐出的临界点为：

（6）

利用（6）式我们可以测量透明材料的厚度和折射率，同时由上式符号可以看出，插入材料后，M1向外移动才能找到条纹吞入和吐出的临界点。

1.2 实验内容及结果

我们采用He-Ne激光器作为光源，如图1布置光路，采用同一批次的多块透明冕玻璃板作为待测材料，测得数据及结果如下，其中d1代表插入材料前条纹吞入和吐出的临界点，d2代表插入材料后条纹吞入和吐出的临界点，t为游标卡尺测得的玻璃板厚度。

由表1可得，n=1.497，通过查阅文献得到冕玻璃的折射率为1.511，测量误差为-0.9%，在误差允许范围内，测量结果较好。

相反，如果已知材料的折射率，利用公式（6）我们也可以测出材料的厚度，同样利用表1的数据，我们利用冕玻璃的标准折射率1.511代入公式（6），算出的结果如表2所示，其中t为游标卡尺测得的玻璃板厚度，t'为实验测得的玻璃板厚度。

由表2可得，E=-1.9%，平均测量误差绝对值小于2%，测量结果较好。

2  金属杨氏模量的测量

2.1 实验原理

杨氏模量是表征固体力学性质的一个重要参数，在大学物理实验中常用的是静态拉伸法，通过光杠杆对微小长度放大的方法来测定。

设金属丝的原长为L，横截面积为S，沿长度方向施力F后，其长度改变ΔL，则金属丝上单位面积的应力为F/S，单位长度应变为ΔL/L。根据胡克定律，在弹性限度内有

（7）

则■                 （8）

又因为■，则：

（9）

我们计划利用迈克尔孙干涉仪与杨氏模量测定仪相结合来测定金属丝的杨氏模量。实验装置如图3所示。

将被测金属丝一端固定在反射动镜M1上，另一端通过一个滑轮与下方的拉力计相连，该拉力计来自于实验“静态法测量金属的杨氏模量”，可读出拉力数值。通过转动迈克尔孙干涉仪的粗调手轮对金属丝施加拉力，使得动镜M1向内移动一个微小的距离，该距离等于金属丝产生的微小伸长量，此时干涉条纹会有吞吐现象。条紋吞吐的数量Δk与M1移动的距离ΔL关系为：

（10）

通过读取条纹吞吐的数量，再通过拉力计读取拉力的大小F，就可以计算出金属丝的杨氏模量E。

（11）

2.2 实验内容及结果

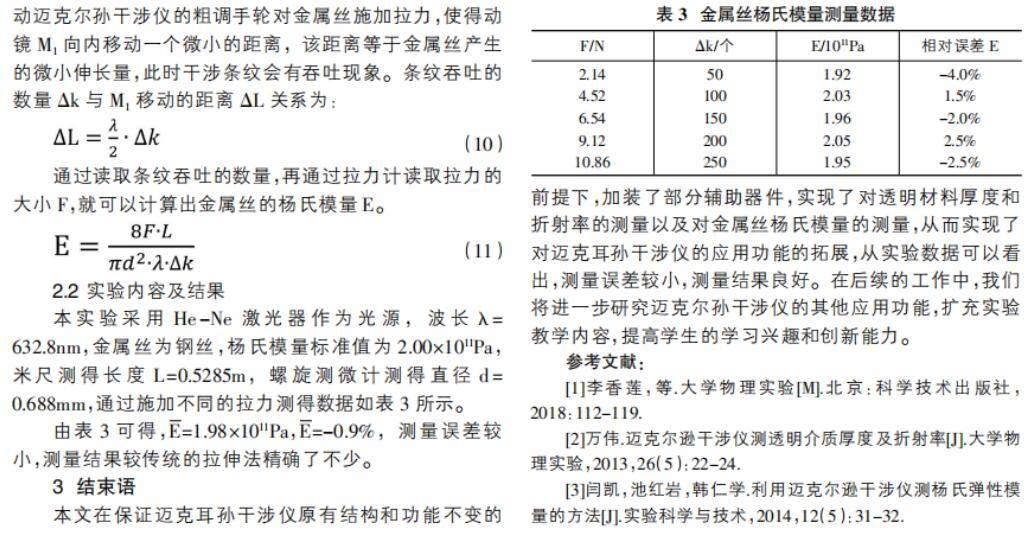
本实验采用He-Ne激光器作为光源，波长λ=632.8nm，金属丝为钢丝，杨氏模量标准值为2.00×1011Pa，米尺测得长度L=0.5285m，螺旋测微计测得直径d=0.688mm，通过施加不同的拉力测得数据如表3所示。

由表3可得，E=1.98×1011Pa，E=-0.9%，测量误差较小，测量结果较传统的拉伸法精确了不少。

3  结束语

本文在保证迈克耳孙干涉仪原有结构和功能不变的前提下，加装了部分辅助器件，实现了对透明材料厚度和折射率的测量以及对金属丝杨氏模量的测量，从而实现了对迈克耳孙干涉仪的应用功能的拓展，从实验数据可以看出，测量误差较小，测量结果良好。在后续的工作中，我们将进一步研究迈克尔孙干涉仪的其他应用功能，扩充实验教学内容，提高学生的学习兴趣和创新能力。

参考文献：

[1]李香莲，等.大学物理实验[M].北京：科学技术出版社，2018：112-119.

[2]万伟.迈克尔逊干涉仪测透明介质厚度及折射率[J].大学物理实验，2013，26（5）：22-24.

[3]闫凯，池红岩，韩仁学.利用迈克尔逊干涉仪测杨氏弹性模量的方法[J].实验科学与技术，2014，12（5）：31-32.