高考数学选择题命题规律及备考策略
2019-12-02高慧明
高慧明
历年高考选择题都特别注重基本知识与基本技能的考查,也侧重于解题的灵活性和快捷性,以“小”和“巧”著称,试题层次性强,一般按照由易到难的顺序排列,能充分体现学生灵活运用知识的能力.
绝大部分数学选择题属于低中档题,且一般按由易到难的顺序排列,主要的数学思想和数学方法能通过它得到充分的体现和应用,并且因为它还有相对难度(如思维层次、解题方法的优劣选择,解题速度的快慢等),所以选择题已成为具有较好区分度的基本题型之一.
选择题具有概括性强、知识覆盖面广、小巧灵活及有一定的综合性和深度等特点,且每一题几乎都有两种或两种以上的解法,能有效地检测学生的思维层次及观察、分析、判断和推理能力.
目前高考数学选择题采用的是一元选择题(即有且只有一个正确答案),由选择题的结构特点,决定了解选择题除常规方法外还有一些特殊的方法.解选择题的基本原则是:“小题不能大做”,要充分利用题目中(包括题干和选项)提供的各种信息,排除干扰,利用矛盾,作出正确的判断.
选择题注重多个知识点的小型综合,渗透各种数学思想和方法,体现以考查“四基”为重点的导向,能否在选择题上获取高分,对高考数学成绩影响重大. 解答选擇题的基本要求是四个字——准确、快捷.选择题主要考查基础知识的理解、基本技能的熟练、基本计算的准确、基本方法的运用、考虑问题的严谨、解题速度的快捷等方面. 解答选择题的基本策略是:要充分利用题设和选择支两方面提供的信息作出判断.一般说来,能定性判断的,就不再使用复杂的定量计算;能使用特殊值判断的,就不必采用常规解法;能使用间接法解的,就不必采用直接解;对于明显可以否定的选择应及早排除,以缩小选择的范围;对于具有多种解题思路的,宜选最简解法等. 解题时应仔细审题、深入分析、正确推演、谨防疏漏;初选后认真检验,确保准确.
解数学选择题主要分直接法和间接法两大类. 直接法是解答选择题最基本、最常用的方法;但高考的题量较大,如果所有选择题都用直接法解答,不但时间不允许,甚至有些题目根本无法解答. 因此,我们还要掌握一些特殊的解答选择题的方法. 解答选择题的基本策略:充分利用题设和选择支两方面所提供的信息作出判断,一般有两种思路:一是从题干出发考虑探求结果;二是从题干和选择支联合考虑或从选择支出发探求是否满足题干条件;先定性后定量,先特殊后推理,先间接后直接,先排除后求解,一般来说要小题巧解,避免小题大做.
本文就从选择题的基本方法来做一些讨论,有些试题除了文中所列举的方法外可能还有许多其他简洁的方法.
一、解答选择题的基本方法
1. 直接法
直接从题设条件出发,运用有关概念、性质、定理、法则和公式等知识,通过严密地推理和准确地运算,从而得出正确的结论,然后对照题目所给出的选项“对号入座”,作出相应的选择.涉及概念、性质的辨析或运算较简单的题目常用直接法.
例1. (1)在△ABC中,内角A, B, C的对边分别为a, b,c,若a=3,b=2■,B=2A,则cos A的值为( )
A. ■B. ■C. ■D. ■
(2)某班有6位学生与班主任老师毕业前夕留影,要求班主任站在正中间且女生甲、乙不相邻,则排法的种数为( )
A. 96B. 432C. 480D. 528
解析:(1)在△ABC中,■=■,∴■=■=■=■,∴ cosA=■.
(2)当甲、乙在班主任两侧时,甲、乙两人有3×3×2种排法,共有3×3×2×24种排法;当甲乙在班主任同侧时,有4×24种排法,因此共有排法3×3×2×24+4×24=528(种).
答案:(1)A;(2)D.
点评:涉及概念、性质的辨析或运算较简单的题目常用直接法. 只要推理严谨,运算正确必能得出正确的答案. 平时练习中应不断提高用直接法解选择题的能力,不能一味地求快,导致快中出错.
相关链接1.(1)数列{an}满足a1=2,an=■,其前n项积为Tn,则T10等于( )
A. ■B. -■C. 6D. -6
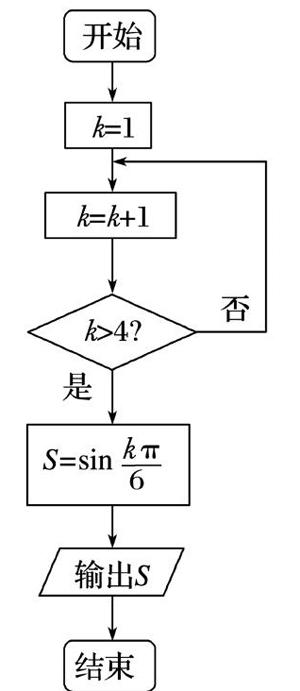
(2)执行如图所示的程序框图,输出S的值为( )
A. -■ B. ■
C. -■ D. ■
答案:(1)D;(2)D.
解析:(1)由an=■?圯an+1=■,所以a2=-3,a3=-■,a4=■,a5=2,a6=-3,…,由此可知数列{an}的项具有周期性,且周期为4,第一周期内的四项之积为1,则a9=a1=2,a10=a2=-3,所以数列{an}的前10项之积为1×1×2×(-3)=-6.
(2)每次循环的结果依次为:k=2,k=3,k=4,k=5>4,∴ S=sin■=■. 故选D.
2. 特例法
从题干(或选项)出发,通过选取特殊情况代入,将问题特殊化或构造满足题设条件的特殊函数或图形位置,进行判断. 特殊化法是“小题小做”的重要策略,要注意在怎样的情况下才可使用. 特殊情况可能是:特殊值、特殊点、特殊位置、特殊函数等.
例2.(1)设f(x)=x-a2,x≤0x+■+a,x>0 若f(0)是f(x)的最小值,则a的取值范围为( )
A. [-1, 2] B. [-1, 0] C. [1, 2] D. [0, 2]
(2)已知等比数列{an}满足an>0,n=1,2,3,…,且a5·a2n-5=22n(n≥3),当n≥1时,log2a1+log2a3+…+log2a2n-1等于( )
A. n(2n-1)B. (n+1)2C. n2D. (n-1)2
解析:(1)若a=-1,则f(x)=x+12,x≤0x+■-1,x>0
易知f(-1)是f(x)的最小值,排除A,B.
若a=0,则f(x)=x2,x≤0x+■-1,x>0易知f(0)是f(x)的最小值,故排除C,D正确.
(2)因为a5·a2n-5=22n(n≥3),所以令n=3,代入得a5·a1=26.
再令数列为常数列,得每一项为8,则log2a1+log2a3+log2a5=9=32.
结合选项可知只有C符合要求.
答案:(1)D;(2)C.
点评:特例法具有简化运算和推理的功效,比较适用于题目中含有字母或具有一般性结论的选择题,但用特例法解选择题时,要注意以下两点:
第一,取特例尽可能简单,有利于计算和推理;
第二,若在不同的特殊情况下有两个或两个以上的结论相符,则应选另一特例情况再检验,或改用其他方法求解.
相关链接2.(1)已知O是锐角△ABC的外接圆圆心,∠A=60°,■·■+■·■=2m·■,则m的值为( )
A. ■B. ■C. 1D. ■
(2)如图,在棱柱的侧棱A1A和B1B上各有一动点P、Q满足A1P=BQ,过P、Q、C三点的截面把棱柱分成两部分,则其体积之比为( )
A. 3∶1B. 2∶1
C. 4∶1D. ■∶1
答案:(1)A;(2)B.
解析:(1)如图,当△ABC为正三角形时,A=B=C=60°,取D为BC的中点,■=■■,则有■■+■■=2m·■,∴■(■+■)=2m×■■,
∴ ■·2■=■m■,∴ m=■,故选A.
(2)将P、Q置于特殊位置:P→A1,Q→B,此时仍满足条件A1P=BQ(=0),则有VC -AA■B=VA■-ABC =■. 故选B.
3. 排除法
排除法就是充分运用选择题中单选题的特征,即有且只有一个正确选择项这一信息,从选择项入手,根据题设条件与各选择项的关系,通过分析、推理、计算、判断,对选择项进行排除,将其中与题设矛盾的干扰项逐一排除,从而获得正确结论的方法. 一般选择支与题干或常识矛盾,选择支互相矛盾时用排除法.
例3.(1)根据下面给出的2004年至2013年我国二氧化硫排放量(单位:万吨)柱形图. 以下结论不正确的是( )
A. 逐年比较,2008年减少二氧化硫排放量的效果最显著
B. 2007年我国治理二氧化硫排放显现成效
C. 2006年以来我国二氧化硫年排放量呈减少趋势
D. 2006年以来我国二氧化硫年排放量与年份正相关
(2)已知函数f(x)=x(1+a|x|). 设关于x的不等式f(x+a) A.(■,0) B.(■,0) C.(■,0)∪(0,■) D.(-∞,■) 解析:(1)从2006年,将每年的二氧化硫排放量与前一年作差比较,得到2008年二氧化硫排放量与2007年排放量的差最大,A选项正确;2007年二氧化硫排放量较2006年降低了很多,B选项正确;虽然2011年二氧化硫排放量较2010年多一些,但自2006年以来,整体呈递减趋势,即C选项正确;自2006年以来我国二氧化硫年排放量与年份负相关,D选项错误,故选D. (2)当x=0时,有f(a) 答案:(1)D;(2)A. 点评:排除法适应于定性型或不易直接求解的选择题.当题目中的条件多于一个时,先根据某些条件在选项中找出明显与之矛盾的予以否定,再根据另一些条件在缩小选项的范围内找出矛盾,这样逐步筛选,直到得出正确的答案. 相关链接3.(1)设函数若f(x)=log2x,x>0log■(-x),x<0 f(a)>f(-a),则实数a的取值范围是( ) A. (-1,0)∪(0,1) B. (-∞,-1)∪(1,+∞) C. (-1,0)∪(1,+∞) D. (-∞,-1)∪(0,1) (2)已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<■)的最小正周期是π,若将其图像向右平移■个单位后得到的图像关于原点对称,则函数f(x)的图像( ) A. 關于直线x=■对称 B. 关于直线x=■对称 C. 关于点(■,0)对称 D. 关于点(■,0)对称 答案:(1)C;(2)B. 解析:(1)取a=2验证满足题意,排除A、D,取a=-2验证不满足题意,排除B. ∴正确选项为C. (2)∵ f(x)的最小正周期为π,∴ ■=π,ω=2. ∴ f(x)的图像向右平移■个单位后得到g(x)=sin[2(x-■)+φ]=sin(2x-■+φ)的图像. 又g(x)的图像关于原点对称,∴-■+φ=kπ,k∈Z,φ=■+kπ,k∈Z. 又|φ|<■,∴|■+kπ|<■,∴k=-1,φ=-■, ∴f(x)=sin(2x-■),当x=■时,2x-■=-■,∴A,C错误,当x=■时,2x-■=■,∴ B正确,D错误. 4. 数形结合法 根据命题条件中的函数关系或几何意义,作出函数的图像或几何图形,将数的问题(如解方程、解不等式、判断单调性、求取值范围等)与某些图形结合起来,利用图像的直观性,化抽象为直观,化直观为精确,从而使问题得到解决,这种方法称为数形结合法. 例4. 若直角坐标平面内的两点P,Q满足条件:①P,Q都在函数y=f(x)的图像上;②P,Q关于原点对称,则称点对[P, Q]是函数y=f(x)的一对“友好点对”(注:点对[P, Q]与[Q, P]看作同一对“友好点对”). 已知函数f(x)=log2x, x>0-x2-4x,x≤0则此函数的“友好点对”有( ) A. 0对B. 1对C. 2对D. 3对 解析:根据题意,将函数f(x)=-x2-4x(x≤0)的图像绕原点旋转180°后,得到的图像所对应的解析式为y=x2-4x(x≥0),再作出函数y=log2x(x>0)的图像,如图所示. 由题意,知函数y=x2-4x(x>0)的图像与函数f(x)=log2x(x>0)的图像的交点个数即为“友好点对”的对数. 由图可知它们的图像交点有2个,所以此函数的“友好点对”有2对. 答案:C. 点评:数形结合法是依靠图形的直观性进行分析的,用这种方法解题比直接计算求解更能抓住问题的实质,并能迅速地得到结果.使用数形结合法解题时一定要准确把握图形、图像的性质,否则会因为错误的图形、图像得到错误的结论. 相关链接4.(1)已知非零向量■,■,■满足■+■+■=0,向量■,■的夹角为120°,且|■|=2|■|,则向量 ■ 与 ■ 的夹角为( ) A. 60°B. 90°C. 120°D. 150° (2) 已知函数f(x)=-x2+2x,x≤0lnx+1,x>0若|f(x)|≥ax,则a的取值范围是( ) A. (-∞,0] B. (-∞,1] C. [-2, 1] D. [-2, 0] 答案:(1)B;(2)D. 解析:(1)如图,因为〈■,■〉=120°,|■|=2|■|,■+■+■=0,所以在△OBC中,BC与CO的夹角为90°,即a与c的夹角为90°. (2)函数y=|f(x)|的图像如图所示. ①当a=0时,|f(x)|≥ax显然成立. ②当a>0时,只需在x>0时,ln(x+1)≥ax成立. 比较对数函数与一次函数y=ax的增长速度. 显然不存在a>0使ln(x+1)≥ax在x>0上恒成立. ③當a<0时,只需x<0,x2-2x≥ax成立,即a≥x-2成立,∴ a≥-2. 综上所述:-2≤a≤0. 故选D. 5. 构造法 构造法是一种创造性思维,是综合运用各种知识和方法,依据问题给出的条件和结论给出的信息,把问题作适当的加工处理,构造与问题相关的数学模式,揭示问题的本质,从而沟通解题思路的方法. 例5. 已知函数f(x)是定义在R上的可导函数,且对于?坌x∈R,均有f(x)>f ′(x),则有( ) A. e2018f(-2018) B. e2018f(-2018) C. e2018f(-2018)>f(0),f(2018)>e2018f(0) D. e2018f(-2018)>f(0),f(2018) 解析:构造函数g(x)=■,则g′(x)=■= ■, 因为?坌x∈R,均有f(x)>f ′(x),并且ex>0,所以g′(x)<0,故函数g(x)=■在R上单调递减, 所以g(-2018)>g(0),g(2018) f(2018) 点评:构造法求解时需要分析待求问题的结构形式,特别是研究整个问题复杂时,单独摘出其中的部分进行研究或者构造新的情景进行研究. 相关链接5.(1)设函数f ′(x)是奇函数f(x)(x∈R)的导函数,f(-1)=0,当x>0时,xf ′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是( ) A. (-∞,-1)∪(0,1) B. (-1,0)∪(1,+∞) C. (-∞,-1)∪(-1,0) D. (0,1)∪(1,+∞) (2)若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,给出下列五个命题: ①四面体ABCD每组对棱相互垂直; ②四面体ABCD每个面的面积相等; ③从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°而小于180°; ④连接四面体ABCD每组对棱中点的线段相互垂直平分; ⑤从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长. 其中正确命题的个数是( ) A. 2B. 3C. 4D. 5 答案:(1)A;(2)B. 解析:(1)(因为f(x)(x∈R)为奇函数,f(-1)=0,所以f(1)=-f(-1)=0. 当x≠0时,令g(x)=■,则g(x)为偶函数,且g(1)=g(-1)=0. 则当x>0时,g′(x)=(■)′=■<0,故g(x)在(0, +∞)上为减函数,在(-∞, 0)上为增函数. 所以在(0, +∞)上,当0 (2)构造长方体,使三组对棱恰好是长方体的三组平行面中异面的对角线,在此背景下,长方体的长、宽、高分别为x、y、z. 对于①,需要满足x=y=z,才能成立; 因为各个面都是全等的三角形(由对棱相等易证),则四面体的同一顶点处对应三个角之和一定恒等于180°,故②成立,③显然不成立; 对于④,由长方体相对面的中心连线相互垂直平分判断④成立; 从每个顶点出发的三条棱的长恰好分别等于各个面的三角形的三边长,⑤显然成立.故正确命题有②④⑤. 6. 估算法 由于选择题提供了唯一正确的选项,解答又无需过程,因此,有些题目不必进行准确的计算,只需对其数值特点和取值界限作出适当的估计,便能作出正确的判断,这就是估算法.估算法往往可以减少运算量,但是加强了思维的層次. 例6.(1)图中阴影部分的面积S是h的函数(0≤h≤H),则该函数的大致图像是( ) (2)已知三棱锥S-ABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此棱锥的体积是( ) A. ■ B. ■ C. ■ D. ■ 解析:(1)由题图知,随着h的增大,阴影部分的面积S逐渐减小,且减小得越来越慢,结合选项可知选B. (2)容易得到△ABC的面积为■,而三棱锥的高一定小于球的直径2,所以V<■×■×2=■,立即排除B、C、D,答案选A. 答案:(1)B;(2)A. 点评:估算法一般包括范围估算,极端值估算和推理估算.当题目从正面解析比较麻烦,特值法又无法确定正确的选项时(如难度稍大的函数的最值或取值范围、函数图像的变化等问题)常用此种方法确定选项. 相关链接6.(1)已知x1是方程x+lg x=3的根,x2是方程x+10x=3的根,则x1+x2等于( ) A. 6 B. 3 C. 2 D. 1 (2)在区间[0,1]上随机取两个数x,y,记p1为事件“x+y≤■”的概率,p2为事件“xy≤■”的概率,则( ) A. p1<p2<■ B. p2<■<p1 C. ■<p2<p1 D. p1<■<p2 答案:(1)B;(2)D. 解析:(1)因为x1是方程x+lg x=3的根,所以2<x1<3,x2是方程x+10x=3的根,所以0<x2<1,所以2<x1+x2<4. 故B正确. (2)在直角坐标系中,依次作出不等式0≤x≤1,0≤y≤1,x+y≤■,xy≤■的可行域如图所示:依题意,p1=■,p2=■, 而■=■,所以p1<■<p2. 故选D. 二、解答选择题的几种特色运算: 1. 借助结论——速算 例7. 棱长都为■的四面体的四个顶点在同一球面上,则此球的表面积为( ) A. 3?仔 B. 4?仔 C. 3■ D. 6?仔 解析:借助立体几何的两个熟知的结论:(1)一个正方体可以内接一个正四面体;(2)若正方体的顶点都在一个球面上,则正方体的对角线就是球的直径. 可以快速算出球的半径R=■,从而求出球的表面积为3?仔,故选A. 2. 借用选项——验算 例8. 若x,y满足3x+y≥12,2x+9y≥36,2x+3y≥24,x≥0,y≥0, 则使得z=3x+2y的值最小的(x,y)是( ) A. (4.5,3) B. (3,6) C. (9,2) D. (6,4) 解析:把各选项分别代入条件验算,易知B项满足条件,且z=3x+2y的值最小,故选B. 3. 极限思想——不算 例9. 正四棱锥相邻侧面所成的二面角的平面角为?琢,侧面与底面所成的二面角的平面角为?茁,则2cos?琢+cos2?茁的值是( ) A. 1 B. 2 C. -1 D. ■ 解析:当正四棱锥的高无限增大时,?琢→90°,?茁→90,则2cos?琢+cos2?茁→2cos90°+cos180°=-1. 故选C. 4. 平几辅助——巧算 例10. 在坐标平面内,与点A(1, 2)距离为1,且与点B(3, 1)距离为2的直线共有( ) A. 1条B. 2条C. 3条D. 4条 解析:选项暗示我们,只要判断出直线的条数就行,无须具体求出直线方程. 以A(1, 2)为圆心,1为半径作圆A,以B(3, 1)为圆心,2为半径作圆B. 由平面几何知识易知,满足题意的直线是两圆的公切线,而两圆的位置关系是相交,只有两条公切线. 故选B. 5. 活用定义——活算 例11. 若椭圆经过原点,且焦点F1(1, 0),F2(3, 0),则其离心率为( ) A. ■ B. ■ C. ■ D. ■ 解析:利用椭圆的定义可得2a=4,2c=2,故离心率e=■=■. 故选C. 6. 发现隐含——少算 例12. y=kx+2与x2+■=1交于A、B两点,且kOA+kOB=3,则直线AB的方程为( ) A. 2x-3y-4=0 B. 2x+3y-4=0 C. 3x+2y-4=0 D. 3x-2y-4=0 解析:解此题具有很大的迷惑性,注意题目隐含直线AB的方程就是y=kx+2,它过定点(0, 2),只有C项满足. 故选C. 7. 利用常识——避免计算 例13. 我国储蓄存款采取实名制并征收利息税,利息税由各银行储蓄点代扣代收. 某人在2001年9月存入人民币1万元,存期一年,年利率为2.25%,到期时净得本金和利息共计10180元,则利息税的税率是( ) A. 8%B. 20%C. 32%D. 80% 解析:生活常识告诉我们利息税的税率是20%. 故选B. 三、选择题中的隐含信息挖掘 1. 挖掘“词眼” 例14. 过曲线S∶y=3x-x3上一点A(2,-2)的切线方程为( ) A. y=-2 B. y=2 C. 9x+y-16=0 D. 9x+y-16=0或y=-2 错解:f/(x)=-3x2+3,f/(2)=-9,从而以A点为切点的切线的斜率为-9,即所求切线方程为9x+y-16=0. 故选C. 剖析:上述错誤在于把“过点A的切线”当成了“在点A处的切线”,事实上当点A为切点时,所求的切线方程为9x+y-16=0,而当A点不是切点时,所求的切线方程为y=-2. 故选D. 2. 挖掘背景 例15. 已知x∈R,a∈R,a为常数,且f(x+a) = ■,则函数f(x)必有一周期为( ) A. 2aB. 3aC. 4aD. 5a 分析:由于tan(x+■)=■,从而函数f(x)的一个背景为正切函数tanx,取a=■,可得必有一周期为4a. 故选C. 3. 挖掘范围 例16. 设tan?琢、tan?茁是方程x3+3■x+4=0的两根,且?琢∈(-■, ■),?茁∈(-■, ■),则?琢+?茁的值为( ) A. -■B. ■C. ■或-■D. -■或■ 错解:易得tan(?琢+?茁)=■,又?琢∈(-■, ■), ?茁∈(-■,■),?琢+?茁∈(-?仔, ?仔),从而?琢+?茁=■或-■. 故选C. 剖析:事实上,上述解法是错误的,它没有发现题中的隐含范围. 由韦达定理知tan?琢+tan?茁<0,tan?琢tan?茁>0,故tan?琢<0,且tan?茁<0. 从而?琢∈(-■, 0),?茁∈(-■, 0),故?琢+?茁=-■. 故选A. 4. 挖掘伪装 例17. 若函数f(x)=loga(x2-ax+3)(a>0且a≠1),满足对任意的x1、x2,当时x1 A. (0, 1)∪(1, 3) B. (1, 3) C. (0, 1)∪(1, 2■) D. (1, 2■) 分析:“对任意的x1、x2,当x1 5. 挖掘思想 例18. 方程2x-x2=■的正根个数为( ) A. 0 B. 1 C. 2 D. 3 分析:本题考生很容易去分母得2x2-x3=2,然后解方程,不易实现目标. 事实上,只要利用数形结合的思想,分别画出y=2x-x2,y=■的图像,容易发现在第一象限没有交点. 故选A. 6. 挖掘数据 例19. 定义函数y=f(x),x∈D,若存在常数C,对任意的x1∈D,存在唯一的x2∈D,使得■=C,则称函数f(x)在D上的均值为C. 已知f(x)=lg x,x∈[10,100],则函数f(x)=lg x在x∈[10,100]上的均值为( ) A. ■ B. ■ C. ■D. 10 分析:■=■=C,从而对任意的x1∈[10,100],存在唯一的x2∈[10,100],使得x1,x2为常数. 充分利用题中给出的常数10, 100. 令x1x2 =10×100=1000,当x1∈[10, 100]时,x2 =■∈[10, 100],由此得C=■=■. 故选A. 四、解答选择题时的常见失误 1. 审题不慎 例20. 設集合M={直线},P={圆},则集合M∩P中的元素的个数为( ) A. 0 B. 1 C. 2 D. 0或1或2 误解:因为直线与圆的位置关系有三种,即交点的个数为0或1或2个,所以M∩P中的元素的个数为0或1或2. 故选D. 剖析:本题的失误是由于审题不慎引起的,误认为集合M,P就是直线与圆,从而错用直线与圆的位置关系解题. 实际上,M,P表示元素分别为直线和圆的两个集合,它们没有公共元素. 故选A. 2. 忽视隐含条件 例21. 若sin2x、sinx分别是sin?兹与cos?兹的等差中项和等比中项,则cos2x的值为( ) A. ■ B. ■ C. ■ D. ■ 误解:依题意有2sin2x=sin?兹+cos?兹…①,sin2x=sin?兹cos?兹…② 由①2-②×2,得4cos22x-cos2x-2=0,解得cos2x=■. 故选C. 剖析:本题失误的主要原因是忽视了三角函数的有界性这一隐含条件. 事实上,由sin2x=sin?兹cos?兹,得cos2x=1-sin2?兹≥0,所以■不合题意. 故选A. 3. 概念不清 例22. 已知l1 ∶ 2x+my-2=0,l2 ∶ mx+2y-1=0,且l1⊥l2,则m的值为( ) A. 2 B. 1 C. 0 D. 不存在 误解:由l1⊥l2,得k1k2=-1. ∴-■·(■)=-1,方程无解,m不存在. 故选D. 剖析:本题的失误是由概念不清引起的,即l1⊥l2,则k1k2=-1,是以两直线的斜率都存在为前提的. 若一直线的斜率不存在,另一直线的斜率为0,则两直线也垂直. 当m=0时,显然有l1⊥l2;若m≠0时,由前面的解法知m不存在. 故选C. 4. 忽略特殊性 例23. 已知定点A(1,1)和直线l ∶ x+y-2=0,则到定点A的距离与到定直线l的距离相等的点的轨迹是( ) A. 椭圆B. 双曲线C. 抛物线D. 直线 误解:由抛物线的定义可知,动点的轨迹是抛物线. 故选C. 剖析:本题的失误在于忽略了A点的特殊性,即A点落在直线l上. 故选D. 5. 思维定势 例24. 如图1,在正方体AC1中盛满水,E、F、G分别为A1B1、BB1、BC1中点. 若三个小孔分别位于E、F、G三点处,则正方体中的水最多会剩下原体积的( ) A. ■B. ■C. ■D. ■ 误解:设平面EFG与平面CDD1C1交于MN,则平面EFMN左边的体积即为所求,由三棱柱B1EF—C1NM的体积为■V正方体,故选B. 剖析:在图2中的三棱锥ABCD中,若三个小孔E、F、G分别位于所在棱的中点处,则在截面EFG下面的部分就是盛水最多的. 本题的失误在于受图2的思维定势,即过三个小孔的平面为截面时分成的两部分中,较大部分即为所求.事实上,在图1中,取截面BEC1时,小孔F在此截面的上方,VB■-BEC■=■V正方体,故选A. 数学选择题的求解,一般有两条思路:一是从题干出发考虑,探求结果;二是从题干和选择支联合考虑或从选择支出发探求是否满足题干条件. 解答数学选择题的主要方法包括直接对照法、概念辨析法、图像分析法、特例检验法、排除法、逆向思维法等,这些方法既是数学思维的具体体现,也是解题的有效手段. 以上的解法,能有效地检测学生的思维层次及观察、分析、判断和推理能力. 小题不能大做、不要不管选项、能定性分析就不要定量计算、能特值法就不要常规计算、能间接解就不要直接解、能排除的先排除缩小选择范围. 从考试的角度来看,解选择题只要选对就行,至于用什么“策略”“手段”都是无关紧要的.所以人称可以“不择手段”. 但平时做题时要尽量弄清每一个选择支正确的理由与错误的原因,另外,在解答一道选择题时,往往需要同时采用几种方法进行分析、推理,只有这样,才会在高考时充分利用题目自身提供的信息,化常规为特殊,避免小题大作,真正做到准确和快速. 总之,解答选择题既要看到各类常规题的解题思想原则上都可以指导选择题的解答,但更应该充分挖掘题目的“个性”,寻求简便解法,充分利用选择支的暗示作用,迅速地作出正确的选择. 这样不但可以迅速、准确地获取正确答案,还可以提高解题速度,为后续解题节省时间. 责任编辑 徐国坚
