竖向近断层地震下隔震结构-非结构系统耦合控制研究

刘德稳， 赵 洁， 刘 阳

(1. 西南林业大学 土木工程学院，昆明 650000； 2. 同济大学 土木工程学院，上海 200092)

20世纪80年代提出的水平向基础隔震技术为实现水平方向抗震目标提供了一条有效的途径。在过去的几次地震中基础隔震技术的效果已得到检验，基础隔震技术能够实现减轻水平地震动作用和保障人民生命安全的抗震目标[1-2]。虽然已大量应用的隔震技术是保护建筑结构与非结构系统安全有效的方法，但是大多数隔震技术都不具备隔离竖向地震动的功能。近年来的研究发现，在震中和发震断层附近产生过较强的竖向地震动，其中一些竖向分量幅值与水平分量之比大于2/3，有些甚至超过1。2012年，美国学者与日本防災科学技術研究所(NIED)开展的合作项目中对5层足尺钢结构隔震系统进行了E-Defense振动台试验研究，发现竖向地震动使建筑物内非结构系统遭受了严重损伤破坏[3]，由于现代高层建筑的非结构构件和设备的造价可高达总造价的3/4，其震害的直接损失应引起足够重视[4]。

近年来一些学者对竖向地震动下的隔震结构性能进行了研究，并取得了丰硕的成果。赵亚敏等[5]提出了一种具有较低的竖向刚度和20%左右的竖向等效阻尼比的组合式碟形弹簧竖向隔震支座，采用1/2比例的基础固定模型及竖向隔震模型振动台试验。颜学渊等[6]开发了适合于高层隔震建筑的三类三维隔震抗倾覆支座。贾俊峰等[7]基于铅芯橡胶隔震垫、组合碟形弹簧和钢板阻尼器的各自力学性能特点,设计开发出一种新型的三维隔震装置。王涛等[8]采用厚层橡胶隔震支座，制作三维基础隔震振动台试验模型，对比了隔震模型和非隔震模型在时域和频域的地震响应。魏陆顺等[9]设计了一种新型的三维隔震系统，该系统包括水平隔震层和竖向隔震层，抗摇摆装置安装在竖向隔震层中用于控制结构摇摆反应，对二层钢框架结构模型进行了振动台试验研究。刘文光等[10]基于铅芯橡胶隔震支座的变形及耗能力学性能特点，设计开发出一种新型的倾斜旋转型三维隔震装置。Tomizawa等[11]研发了一种由水平叠层橡胶隔震支座、竖向空气弹簧、滑块组成的三维隔震装置，并应用于东京一所三层钢筋混凝土公寓建筑中。Vu等[12]提出一种分层柔性和阻尼竖向支撑装置减小隔震结构的竖向地震加速度响应的概念，通过9层隔震结构的数值分析证明可显著减小竖向地震加速度反应。尽管目前对结构竖向减震的研究取得了一定进展，但对隔震结构-内部非结构系统的竖向动力性能研究还不充分，特别是如何应对竖向近断层地震动是未来研究的关键难点问题。

为了获得高静态承载和较好的隔振效应，采用准零刚度进行隔振为振动控制提供了一种新的思路。准零刚度的概念最早由Alabuzhev等[13]提出，近年来，采用该原理进行机械设备隔振的研究得到了学者的关注，Carrella等[14]对准零刚度的静力性能进行了研究，Shaw等[15]对准零刚度系统的关键参数进行了研究，Ahn等[16]提出了准零刚度系统的一种广义模型，并对其设计方法进行了研究。尽管对准零刚度的隔振研究取得了较大进展，但进行地震动作用下该系统的抗震性能研究还较少，尤其是近断层地震动作用下。针对该问题，研究竖向近断层地震动作用下的隔震结构-内部非结构系统的性能，重点关注：①竖向近断层地震动下隔震结构内部非结构系统的动力响应特征；②综合考虑隔震结构及其内部非结构的动力特性参数分析采用竖向准零刚度隔震支座对结构的响应控制方法。

1 系统动力模型及运动方程

1.1 隔震系统模型

采用竖向准零刚度系统对非结构系统进行竖向隔震控制。竖向准零刚度隔震系统是由竖向负刚度元件和正刚度元件组合而成从而实现在某一位置或某一区域出现竖向总刚度近似为零的隔震系统。竖向负刚度由斜向的支撑弹性元件运动到一定位置时产生，由于在竖向静力作用下竖向刚度随斜向夹角变化，因此该系统为几何非线性变化系统，刚度与位移相关，且为非线性关系。如图1所示为典型的系统示意图，其中：x为质量块相对于固定端的竖向位移；L为支撑的长度；h为高度；θ为支撑与水平线的夹角，当运动至水平时，即夹角为0时，此时斜向支撑的长度变为a。该模型的恢复力表达式为

(1)

式中：kv为竖向附加刚度；k1为斜向弹簧元件的刚度。

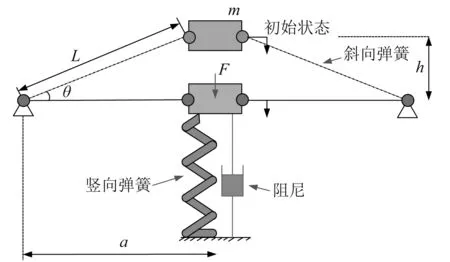
图1 准零刚度隔震支座分析模型Fig.1 Model of QZS bearing

1.2 系统动力方程

如图2所示，建立隔震结构-内部非结构系统的两质点模型，假定：u1为内部非结构系统相对于基底的竖向位移；u2为隔震结构的竖向变形；ug为竖向地震动发生时自由场地面运动；m1，m2分别为隔震结构、内部非结构的质量。在竖向地震动作用下根据动力平衡关系建立如下方程

(2)

(3)

式中：c为隔震结构的竖向阻尼系数；k2为隔震结构的竖向刚度。

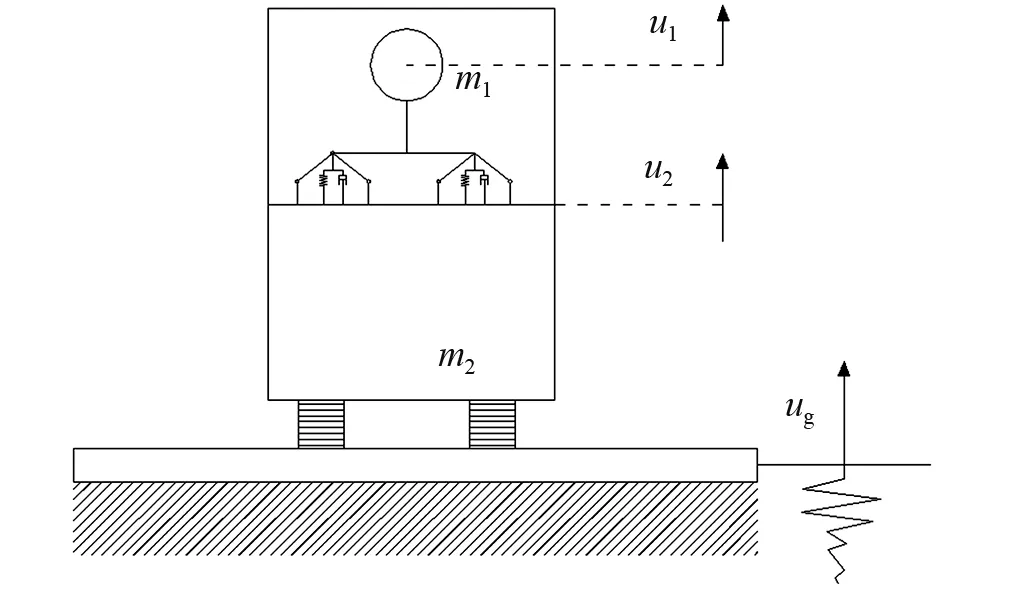
图2 隔震结构-内部非结构系统分析模型Fig.2 Model of seismic isolation structure with QZS

为便于分析，定义如下参数

μ=m1/m2

(4)

(5)

(6)

(7)

(8)

(9)

(10)

式中：ω1，ξ1为非结构附加QZS的竖向自振频率和附加阻尼比；ω2，ξ2为隔震结构的竖向自振频率和阻尼比。

式(2)和式(3)可以改写为

(11)

(12)

1.3 能量平衡

隔震系统通过滤波效应来降低结构响应地震激发和耗散能量从而降低输入能量，这需要依靠结构自身来吸收地震能量，此时需要平衡结构和隔震支座之间的变形，以确定最佳的隔震效果。由于能量涵盖了所有的响应特性，因此能量可提供非常有用的方式去评估隔震结构的性能及其整体结构地震响应特性。建立隔震结构-内部非结构系统的相对能量方程[17]，对于式(11)、式(12)两端同时对d(u1-u2)， du2积分得到

(13)

(14)

任意时刻体系各项能量之和与地震总输入能量满足

EK+ED+EE=EI

(15)

式中：EK，ED和EE为动能、阻尼能和弹性应变能；EI为地震总输入能量。

2 地震波选取

近断层地震动具有方向性效应和永久地面位移效应，一般按震源机制分为方向效应和滑冲效应两类[18-19]。地震波选取原则为：①距离断层间距小于10 km；②震级为6.7～7.6；③剪切波速大于200 m/s。本文根据两类不同的效应并考虑脉冲周期分两组作为地震响应分析的输入条件进行研究，见表1，分别编号为A1，A2，B1，B2。计算时，按8度罕遇地震动进行分析，所有地震动的加速度峰值均调幅为0.4g。如图3所示为所选地震波的位移谱，图4为竖向近断层地震波的输入能量谱。

表1 地震波信息表Tab.1 Earthquake records used in the simulations

图3 竖向近断层地震波的位移谱Fig.3 Displacement spectrum for near-fault earthquakes

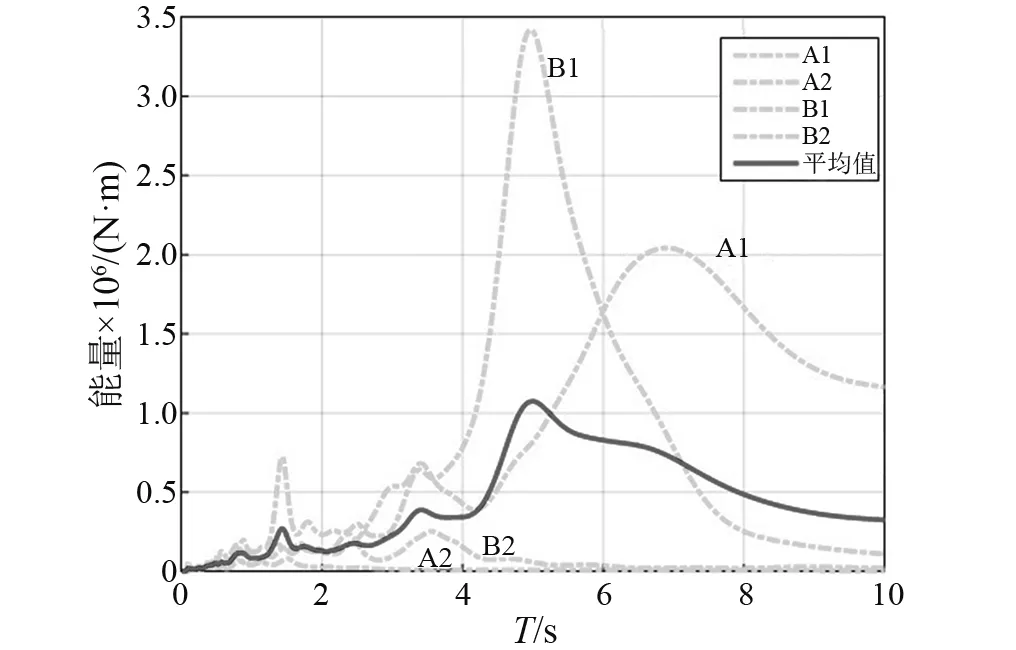
图4 竖向近断层地震波的输入能量谱Fig.4 Input energy spectrum for near-fault earthquakes

3 数值分析

3.1 分析模型的参数选取

3.2 简谐激励

假定水平时系统处于竖向平衡位置，并以该状态作为动力分析的初始状态，平衡位置时建立坐标系，系统运动时根据动力平衡关系建立在简谐激励Acosωt(A为加速度幅值，ω为激励频率)作用下单自由度隔震系统的动力学方程，并进行求解。定义加速度放大系数为

(16)

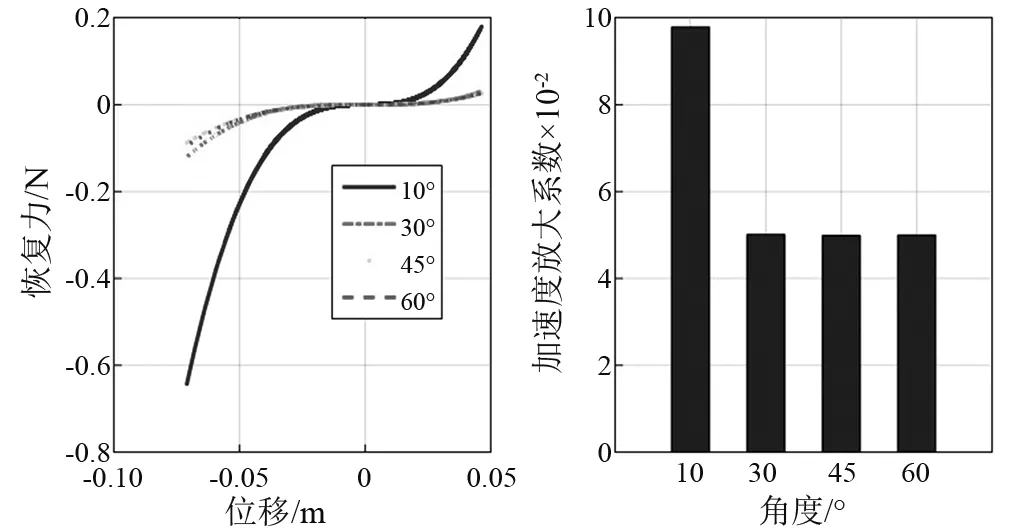
图5 不同角度下非结构元件动力响应计算结果Fig.5 Structural dynamic response results for different degrees

图6 不同竖向自振周期下非结构元件动力响应计算结果Fig.6 Structural dynamic response results for different vertical nature period

3.3 地震时程反应分析

如图7所示，为Chi-Chi TCU51地震波下非结构元件竖向恢复力-位移关系曲线及加速度时程分析曲线。分析中隔震结构竖向自振频率f2=17 Hz，L=0.5 m，β=3.36，γ=0.87，μ=0.01，ξ1=0.10，ξ2=0.05，T1=1.5 s。无控结构的非结构元件竖向自振周期为0.1 s，阻尼比取0.05。竖向恢复力分解为有黏滞阻尼力和弹性力两部分，结果显示其具有饱满的滞回耗能特性，且在零点位置具有准零刚度特性。图7(c)中附加与不附加准零刚度控制系统的非结构元件的加速度对比可知，有控系统具有良好的减震效果。图8为Chi-Chi TCU51地震波下非结构元件竖向加速度时程曲线特征，图9为Chi-Chi TCU51地震波下非结构元件竖向加速度响应的傅里叶谱曲线。由图可知，采用准零刚度控制方法可使高频振动能量降低，其与无控结构的加速度峰值出现时刻、加速度时频响应特征具有显著差异。

图7 非结构元件竖向动力特征Fig.7 Dynamic property for nonstructural component

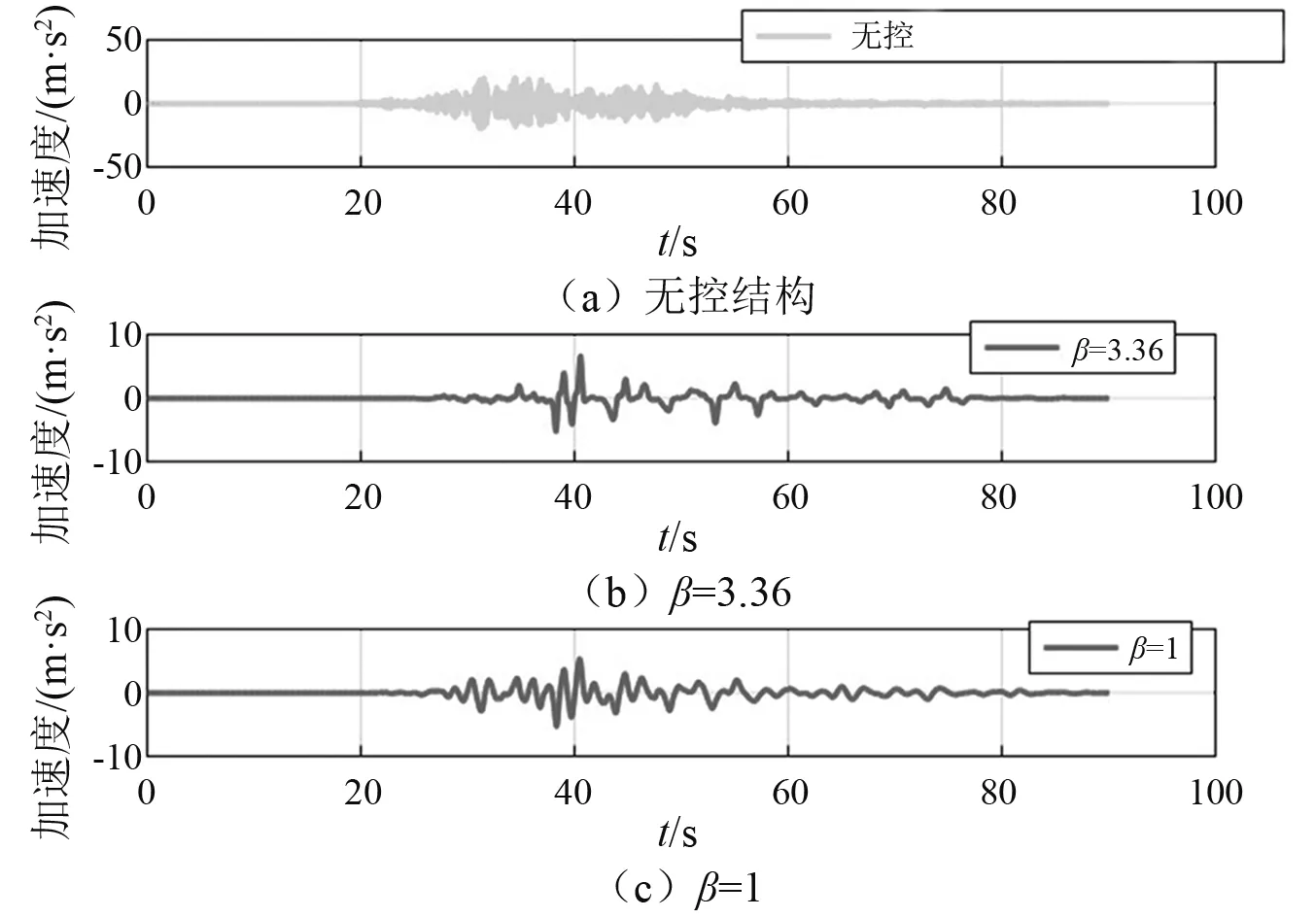
图8 非结构元件竖向加速度时程曲线特征Fig.8 Vertical acceleration time history for nonstructural component

如图10所示，为Chi-Chi TCU51地震的水平分量作用下的地震响应情况。假定分析中隔震结构水平自振周期为2 s，采用双线性模型模拟基础隔震支座，屈服后刚度/初始刚度=0.1，屈服力/重力比为0.02，设备质量为1×103kg，μ=0.001。如图10所示，在近断层水平地震作用下的基础隔震结构隔震层变形较大，但对于基础隔震结构体系而言，其设备系统在水平向具有一定的减震控制效果。

图9 非结构元件竖向加速度响应的傅里叶谱曲线 (Chi-Chi-TCU51)Fig.9 Fourier spectrum for vertical acceleration curve of nonstructural component (Chi-Chi-TCU51)

图10 基础隔震结构水平动力特征(Chi-Chi-TCU51)Fig.10 Dynamic property for horizontal seismic isolation (Chi-Chi-TCU51)

图11～12所示为A组Chi-Chi TCU51及B组Chi-Chi-TCU52地震动作用下无控和有控时对应的非结构元件总能量输入和弹性应变能比较。隔震结构竖向自振频率f2=17 Hz，L=0.5 m，β=3.36，a=0.87，μ=0.01，ξ1=0.10，ξ2=0.05。无控结构的非结构元件竖向自振周期为0.1 s，阻尼比取0.05。由图可知，有控时非结构元件总能量、弹性应变能和阻尼能要大于无控时结构非结构元件对应的总能量。尽管由于结构振动特性的改变造成有控体系总输入能要大于无控体系，但因隔震体系隔震层变形较大，因此其弹性变形能和阻尼耗能能力要强于无控结构。

分析四条地震波无控和有控时对应的非结构元件的加速度放大系数计算结果，如图13所示。隔震结构竖向自振频率f2=17 Hz，L=0.5 m，β=3.36，a=0.87，μ=0.01，ξ1=0.10，ξ2=0.05。无控结构的非结构元件竖向自振周期为0.1 s，阻尼比取0.05。由图13可知，四条地震波作用下，加速度放大系数均小于1，最小为0.089，减震率达90%以上，减震效果显著，此外地震波特性对非结构元件的竖向减震效果有一定影响，但平均放大系数为0.31，可实现良好的震动控制效果。

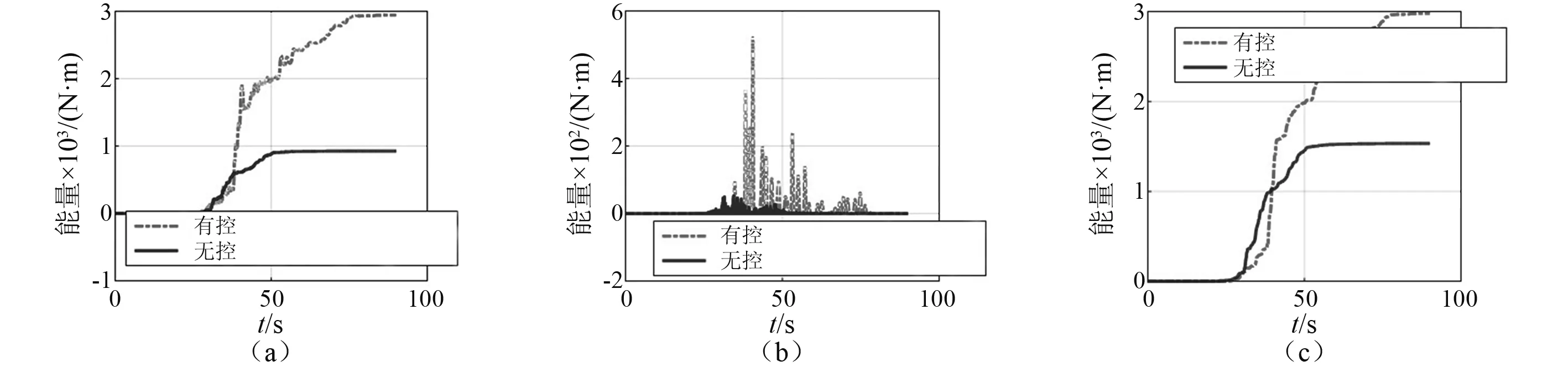
图11 能量时程曲线(A组 Chi-Chi-TCU51)Fig.11 Energy time history for seismic isolated structure (Group A: Chi-Chi-TCU51)

图12 能量时程曲线(B组 Chi-Chi-TCU52)Fig.12 Energy time history for seismic isolated structure (Group B: Chi-Chi-TCU52)

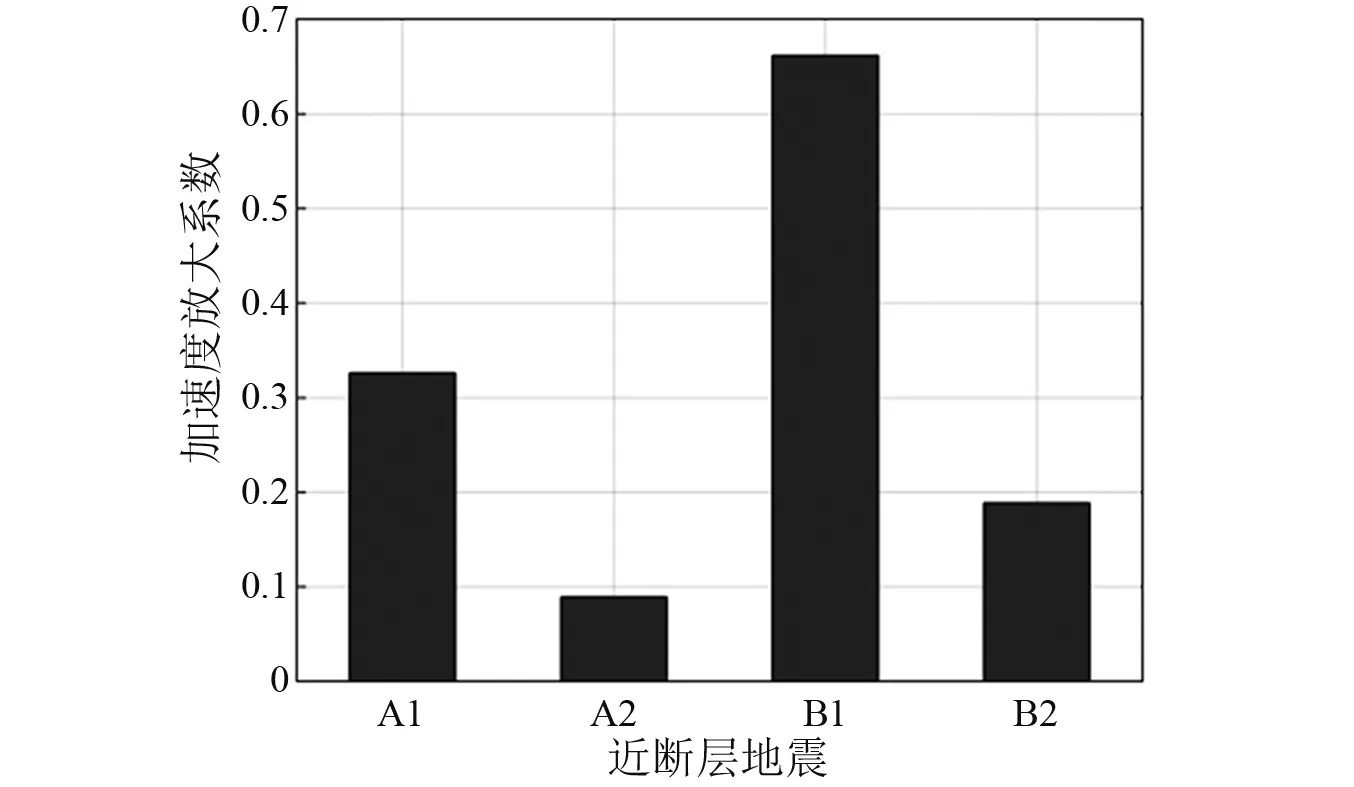
图13 加速度放大系数比较Fig.13 Comparison of acceleration amplification factor

图14所示为两类地震波作用下非结构元件竖向加速度放大系数及竖向变形随隔震结构自振频率变化情况。分析中隔震结构竖向自振频率f2的研究范围为[5，20]Hz，L=0.5 m，γ=0.87，β=3.36，μ=0.01，ξ1=0.10，ξ2=0.05。无控结构的非结构元件竖向自振周期为0.1 s。由图可知两类地震波作用下非结构元件的加速度放大系数小于1，附加QZS的非结构元件具有显著的减震效果，方向效应小于滑冲效应对应的地震响应值。

分析不同竖向阻尼比ξ1下非结构元件的加速度放大系数计算结果，如图15所示。分析中隔震结构竖向自振频率f2的研究范围为[5，20]Hz，L=0.5 m，β=3.36，a=0.87，μ=0.01，ξ1=0.10，ξ2=0.05。无控结构的非结构元件竖向自振周期为0.1 s，阻尼比取0.05。由图可知，竖向地震减震效果与基础隔震结构的竖向自振频率和非结构元件的竖向阻尼有关，在所研究的参数变化范围内，系统的加速度放大系数均小于1，显示非结构元件的地震响应得到了降低。附加阻尼比可根据实际地震响应规律来选取最优的参数值。

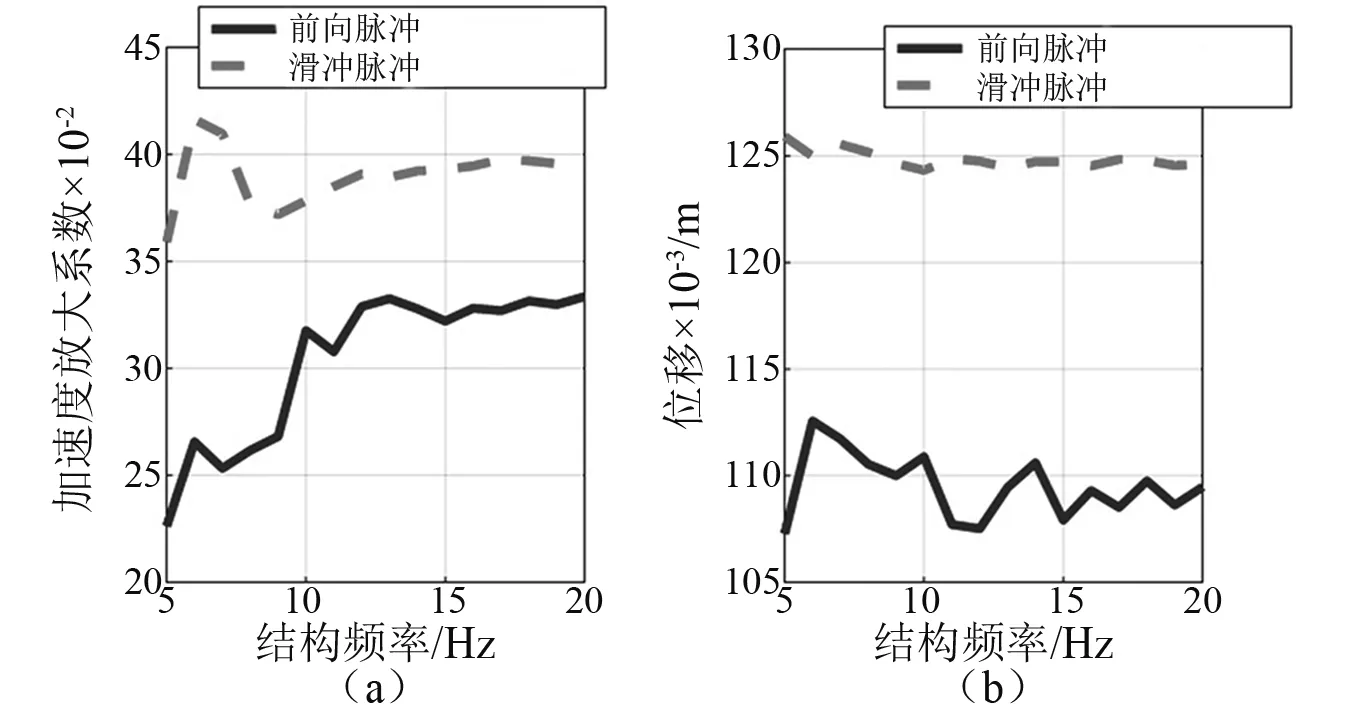
图14 非结构元件的地震响应计算结果Fig.14 Seismic response results of nonstructural component

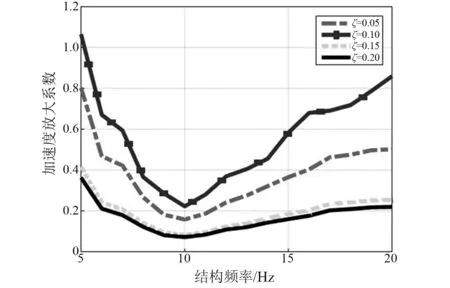
图15 非结构元件不同阻尼比下地震响应计算结果Fig.15 Seismic responses of nonstructural component with different damping ratio

4 结 论

通过采用竖向准零刚度系统进行隔震结构-内部非结构系统的非结构元件地震响应控制，研究结果表明对于常规竖向地震动卓越频率的简谐激励作用下的系统通过选取合理的竖向自振周期能实现良好的隔震效果；竖向近断层地震动作用下的非结构元件的地震响应得到了有效控制。非结构元件的竖向减震效果整体与地震波特性、基础隔震结构的自振频率、非结构元件的自振周期及阻尼比取值有关。

由于静力荷载的不确定性，静力平衡点不一定在水平位置，因此未来可以进一步深入分析不在水平位置作为静力平衡时的地震响应控制机理。