基于区域生长算法的复杂建筑物屋顶点云分割

朱军桃，王 雷，赵 传，郑旭东

(1.桂林理工大学测绘地理信息学院，桂林 541006；2.广西空间信息与测绘重点实验室,桂林 541006；3.信息工程大学地理空间信息学院，郑州 450001)

0 引言

随着机载激光雷达(light detection and ranging,LiDAR)测量技术的不断突破，其应用前景广为人们关注。利用高密度的LiDAR数据构建3D城市模型相比于影像匹配更加容易，而对城市中的建筑物进行模型重建无疑需要对复杂的建筑物屋顶进行精细化分割。由于复杂建筑物的屋顶存在较多大小不一的面片，其点云分布散乱且存在噪声等问题，使现有算法在精确分割建筑物屋顶面时仍面临着严峻挑战。

对建筑物屋顶点云进行分割方法主要包括3类：①基于模型匹配的算法，由于实际中建筑物往往包含多个顶面，随机采样一致性算法(random sample consensus,RANSAC)[1-3]以迭代的方式从含有大量局外点中获得最优的模型参数从而受到广泛关注，但局外点所占比例往往需要以很高迭代次数才能获得最优模型参数，导致时间成本巨大，不利于对复杂建筑物的屋顶面点云分割；②基于特征聚类的算法[4-5]，此类方法通过采样点邻域计算出采样点微分几何属性，几何属性的估算受采样点邻域大小以及测量误差影响，同时其阈值敏感性高，若设置不当就会造成建筑物屋顶面分割效果不理想甚至分割失败；③基于区域生长算法[6-8]的算法，区域生长算法可简单描述为从某种子点开始，以种子点与邻域内点具有某种一致关系划分点集，其中以法向量及曲率划分方式居多，同特征聚类方法一样，由于单个激光点不存在矢量属性，往往以种子点邻域内激光点采用拟合或计算特征值等方式近似表达种子点的法向量或曲率信息等，而邻域的选取与测量误差会直接影响所表征点的矢量信息，种子点的生长过程中邻近点的搜索方式同样可能影响生长结果，此类问题导致了区域生长算法在分割建筑物屋顶点云时易产生错误分割，且各屋顶面交界处采样点难以准确分割。

针对上述区域生长算法中存在激光点矢量信息需要通过邻域估算，生长过程中邻域点选取不当的问题，本文提出一种以三角面为基元的基于区域生长算法的复杂建筑物屋顶点云分割算法。通过构建Delaunay三角网的方式，将屋顶面点云划分至不规则三角网内,以区域生长算法划分各三角面，避免了各激光点逐点进行矢量估算和邻域点选取问题；然后合并各过度划分的面片集合及孤立点，完成对建筑物屋顶面点云的精确分割。

1 研究方法

1.1 面片划分

对于没有任何拓扑信息的点云[9]，Delaunay三角网以最邻近三点形成三角形，各三角形边互不相交的独有优势，无疑成为建立各激光点间关系的良好方式。本文通过构建Delaunay三角网，计算各三角面片单位法向量，并剔除边长过长与法向量异常的三角形。通过建筑物同一面片上各三角面法向量基本相同的特征，以任意三角面作为起始种子面，其单位法向量作为判断条件，种子面的共边三角面作为邻近面，计算与此三角面共边三角面单位法向量的夹角，设置角度阈值α作为生长条件，若夹角小于α，则2个三角面属于同一面片集合；若大于α，则停止此方向生长。采用此方式可避免逐点估算法向量与判断邻近关系。区域生长流程如图1所示。

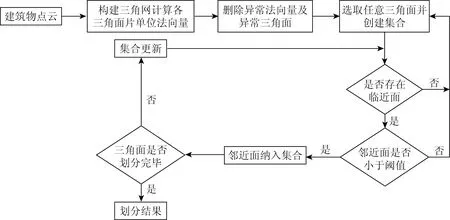
图1 三角面为基元的区域生长流程Fig.1 Flow chart for region growing based on triangles

最终同属相同屋顶面片内的三角面会被划分到同一面片集合中。但测量误差、点云散乱性分布等问题会造成诸多法向量异常的三角面。图2为一人字形屋顶，同一面片集合中出现了异常三角面，且在2个屋顶面交界处数量明显增加。为解决此类过度划分问题，需要对面片集合进行合并。

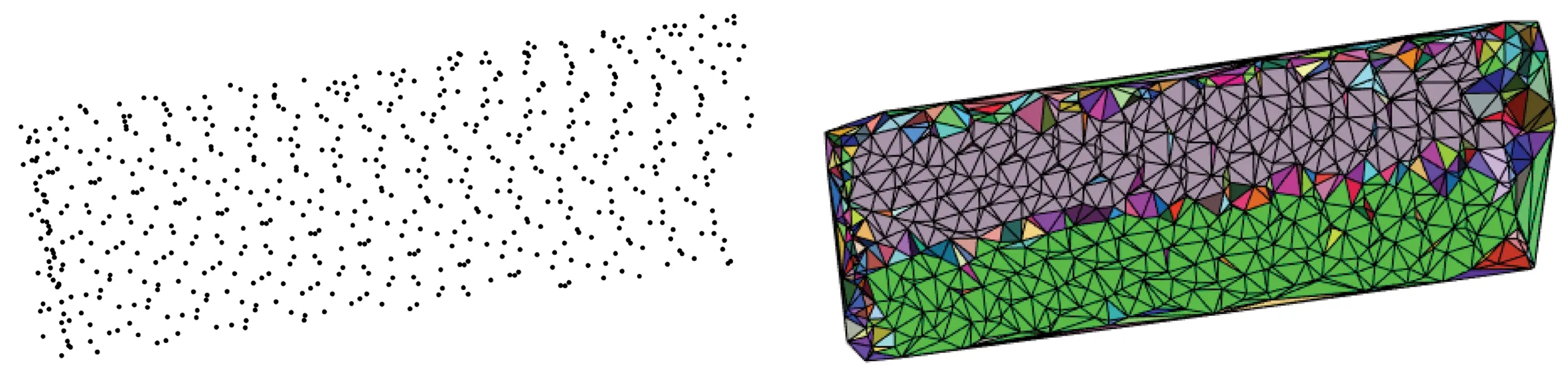
(a)人字形屋顶点云 (b)三角面集合

图2 三角面区域生长结果

Fig.2Resultofregiongrowingoftriangles

1.2 面片合并

依据以三角面为基元的方式，可以部分解决屋顶交界处法向量分布散乱问题。2个屋顶面相交处三角面的3个激光点分别属于不同平面，由于激光点以相邻共边三角形为种子面的邻近面，孤立的三角面各边被不同面片集合所剖分，即将异常三角面上各点划分至不同面片集合，但仍存在未被划分的点与过度分割的面片集合。考虑到测量误差及生长角度阈值α所造成的影响，为更精确获得各面片平面方程，即

Ax+By+Cz+D=0，

(1)

式中A,B,C,D为系数。

采用RANSAC算法计算各面片集合的平面方程。因已经过初步划分的点云极少含有局外点，即少量的迭代次数就能得到最优平面方程，减少时间成本。

在不考虑房屋附属的情况下，认为激光点数量越少的集合越有可能为过度分割的平面，其中具有较大误差点可能性越高,因此本文采取以下策略解决过度分割问题：

1)边界获取。采用Alpha Shape算法获得各集合非凸边缘，具体方法见文献[10]。

2)孤立点合并。将构成平面最少激光点数小于3的点集作为孤立点处理，计算孤立点P到各Alpha Shape边缘距离，若P在Alpha Shape边缘内，距离为0；若P至最近Alpha Shape边缘距离小于阈值Б，则计算点到平面距离L，即

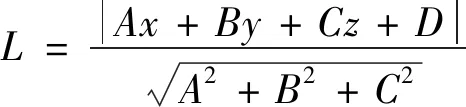
(2)

设定阈值δ，若L≤δ，则将P合并至此面片集合，并更新此集合Alpha Shape边缘；若L>δ，则将P作为噪声点剔除。

3)面片合并。统计各面片集合激光点数量，由大到小排列，并认为激光点数量最多的集合为标准平面。计算标准面至各Alpha Shape边缘距离，若平面在Alpha Shape边缘内，距离为0；若距离小于阈值Б，则计算平面夹角，即

(3)

对于平面夹角阈值，若设置太大，则容易造成某些夹角小的面片过度合并；若设置太小，则容易造成过度剖分的面片难以融合。因此本文依据点集数量对阈值进行改进，计算公式为

ρr=Kρ，

(4)

(5)

式中：Nb为标准面片激光点数量；Nn为邻近面片激光点数量；ρ为平面夹角阈值初值；ρr为最终平面夹角阈值。式(5)依据各集合激光点数量，若数量与标准面片越接近则越可能为真实屋顶面，减小阈值有利于避免过度合并；相反，增大阈值有利于合并因激光点数量少而使噪声被放大的面片；但为了避免夹角阈值过小，设置K≥0.2。

2 实验

2.1 实验数据与参数

本文实验数据来自国际摄影测量与遥感学会(International Society for Photogrammetry and Remote Sensing,ISPRS)提供的德国Vaihingen地区的机载LiDAR点云，点云平均密度约4个/m2，并使用由Yang等[11]分类的建筑物点云数据，使用CloudCompare软件剔除分类错误的激光点。依据文献[4]，法向量角度阈值α选取范围一般为5°～10°，本文选取5°；孤立点与平面到各Alpha Shape边界距离阈值Б应大于点云平均距离，本文选取2倍点云平均距离，为1 m；为保证孤立点与面片正确合并，孤立点到各平面距离阈值δ选取应小于点云平均距离，本文取1/2点云平均距离，设置为0.25 m；2个平面夹角阈值ρ应大于α，本文取10°。

2.2 算法对比

通过对比RANSAC算法与区域生长算法分割的建筑物点云，定量评价本文方法对建筑点云的分割效果。

(a)建筑物1影像 (b)建筑物1 (c)建筑物1 (d)建筑物1

本文方法分割结果 RANSAC分割结果 区域生长分割结果

(e)建筑物2影像 (f)建筑物2 (g)建筑物2 (h)建筑物2

本文方法分割结果 RANSAC分割结果 区域生长分割结果

图3-1 不同算法对建筑物分割效果对比

Fig.3-1Comparisonbetweendifferentalgorithmsonsegmentationofbuildings

(i)建筑物3影像 (j)建筑物3 (k)建筑物3 (l)建筑物3

本文方法分割结果 RANSAC分割结果 区域生长分割结果

(m)建筑物4影像 (n)建筑物4 (o)建筑物4 (p)建筑物4

本文方法分割结果 RANSAC分割结果 区域生长分割结果

图3-2 不同算法对建筑物分割效果对比

Fig.3-2Comparisonbetweendifferentalgorithmsonsegmentationofbuildings

由图3可以看出，RANSAC算法分割建筑物点云，仅追求数学上的一致性，导致平面过度分割，如图3(c)中框选区域；以区域生长算法分割建筑点云，在处理屋脊时处效果欠佳；而以本文方法所获得结果均避免了上述问题。但本文方法在图3(b)中框选处，将本应处于同一平面上的点簇划分成2个平面；由图3(c)和(d)可知，RANSAC算法同样发生此问题，而区域生长算法在此处将大量屋顶面过度融合。在对建筑物2的划分中，图3(f)中各屋檐处存在狭窄平面，最终被划分为主屋顶面的一部分。由此发现，本文处理狭长区域时，由于三角面法向量敏感性，容易导致三角面的关联被异常面截断甚至难以构成三角面，导致狭长的点簇被划分为孤立点而被划分到其他屋顶面上。图3(k)框选处，存在较多误差较大的激光点，RANSAC算法在此处分割出错误平面；图3(l)中此处错分现象更为严重；而图3(j)采用本文方法未受到误差较大的激光点干扰，正确分割了此平面，说明本文方法较RNASAC算法与区域生长算法的抗噪能力更强。

为更加准确地评价本文方法精度，采取文献[12]的评价准则分别对本文方法、RANSAC算法与区域生长算法的分割完整率C、正确率A及分割质量Q进行评估。计算公式分别为

C=TP/(TP+FN)，

(6)

A=TP/(TP+FP)，

(7)

Q=TP/(TP+FN+FP)，

(8)

式中：TP为正确分割激光点数量；FN为漏提激光点数量；FP为错误分割激光点数量。

表1和表2分别为各算法的精度对比和建筑物屋顶面分割数量对比。由表1可知，采用本文方法对建筑物1，3，4的分割完整率、正确率及提取质量均在不同程度上优于RANSAC算法及区域生长算法分割方法，其中对建筑物的分割完整率明显高于后者，由此发现采取本文分割方法有较好的抗噪能力。但建筑物2中所表现的数据，采取本文方法分割效果较差于RANSAC算法，原因是其所含狭长屋顶面较多，最终导致过多的错误分割。由表2可见，对建筑物4的3种方法分割结果相差无几，随着建筑物顶面数量增加，本文分割方法逐渐优于RNASAC算法与区域生长算法，但本文方法建筑物2所分割效果相对较差。

表1 算法精度对比Tab.1 Comparison between accuracies of algorithms (%)

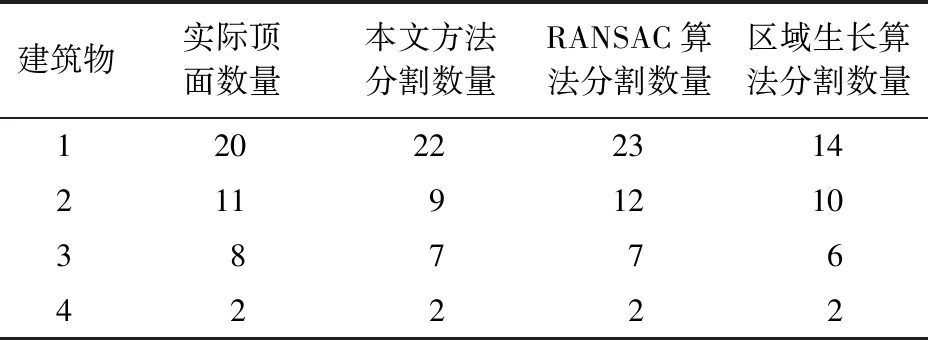
表2 建筑物屋顶面分割数量对比Tab.2 Comparison between quantity of roofs of building in segmentation

3 结论

本文提出了一种以三角面为基元的基于区域生长算法的复杂建筑物屋顶点云分割算法，以构建Delaunay三角网方式构建建筑物点云之间关系，并以各三角面片单位法向量作为判别条件，依据共边三角面单位法向量的相似性对建筑物屋顶点云进行分割。

1)本文方法避免了对各激光点进行法向量估算，且无需建立激光点间的邻近关系，一定程度上简化了传统区域生长算法步骤。

2)虽然本文在屋顶面交界处同区域生长算法一样出现了法向量异常的三角面，但以三角面为基元的分割方式使法向量异常三角面被其邻近面片所剖分，部分地解决了屋顶交界处采样点异常问题。

3)对于仍然存在的一部分孤立点与过度分割的面片，通过RANSAC算法，快速获取各平面方程系数，结合Alpha Shape算法判断孤立点及各平面邻近关系，精确合并了孤立点与过度分割面片。比较于RANSAC算法与传统的区域生长算法，本文方法所获取结果在分割精度与屋顶面分割数量上均更为理想。

4)本文方法不足之处在于，以三角面为基元的分割方式对于狭长的建筑物屋顶面分割效果不理想。该问题将在今后学习研究中完善解决。