大跨度公轨两用斜拉桥梁端轨道结构适应性研究

2019-12-02吴亮秦吴定俊

铁道学报 2019年11期

吴亮秦，吴定俊，李奇

(1. 华东交通大学土木建筑学院，江西南昌 330013； 2. 同济大学土木工程学院，上海 200092)

在公路和城市轨道交通荷载共同作用下，大跨度公轨两用桥梁端将形成较大的转角。以往针对几座公轨两用桥的研究表明[1-3]，大跨度公轨两用桥主跨梁端转角可达5‰，这一转角幅值可保证列车走行性要求，但超过桥上无砟轨道扣件系统可承受的范围，此时，扣件上拔力成为限制梁端转角的控制因素。而梁端转角与桥梁刚度直接相关，若以满足扣件上拔力要求为评判标准来限制这些大跨度公轨两用桥的刚度，将导致建设浪费甚至不可实现。

在实际工程中，为满足梁体构造与伸缩缝设计的需要，大跨轨道桥梁端还普遍存在长悬臂、大梁缝的问题。长悬臂导致在梁端转角很小情况下，扣件上拔力既已超限[4-5]；大梁缝导致梁缝两侧钢轨支承间距扩大，影响轨下刚度的均匀性，甚至可能引起钢轨折断而危及行车安全[6-8]。梁端长悬臂、大梁缝是大跨轨道桥上铺设无砟轨道时所面临的共性问题，必须在梁端采取特殊的轨道结构措施。对此，欧洲提出采用过渡板装置来适应梁端变位与构造要求，这类装置在国内外大跨径轨道桥上均有运用实例，并有一些与之相关的研究[9-11]。但以往研究主要针对整体刚度较大的大跨度铁路桥梁，鲜有研究涉及整体刚度相对较小的城轨桥梁尤其是大跨度公轨两用桥。

本文以某铺设无砟轨道的大跨度公轨两用钢桁梁斜拉桥为工程背景，提出梁端采用过渡板与梯形轨枕两种特殊轨道结构措施，针对梁端转角较大且蕴含大梁缝、长悬臂构造特点的大跨度轨道桥梁梁端扣件受力问题,探讨不同特殊轨道结构措施对其的适应性。

1 有限元模型及梁端变位计算结果

某大跨度公轨两用钢桁梁斜拉桥的桥式布置为(38.25+147+251.4)m，全长436.65 m。上层为双向四车道公路，下层为双线轨道交通，设计活载分别为公路Ⅰ级和地铁B型8节编组列车，上、下层桥面为正交异性钢桥面体系。钢桁梁采用两片主桁布置，总桁宽19.4 m，桁高9.6 m。边跨侧引桥为48 m钢-混凝土结合梁，主跨侧引桥为30 m预应力混凝梁。

建立桥梁有限元模型见图1，桥塔、钢桁、纵横梁、桥墩及桩基采用空间梁单元模拟，钢桥面板按梁格法等效简化；斜拉索采用空间杆单元模拟并用Ernst公式考虑索自重垂曲所致非线性效应；根据群桩位移计算结果，在冲刷线以下10 m将桩底固结。

基于有限元计算模型，按主跨梁端转角影响线最不利位置加载，可得在设计静活载作用下梁端转角最大值为3.86‰ rad(加载后全桥变形情况见图1，图中虚线表示主桥初始位置)。另外计算得到在±30 ℃年温差作用下主跨梁端伸缩量为±136 mm。主跨梁端构造见图2，梁缝初始值为500 mm，可得主跨梁缝变化范围为464～636 mm。

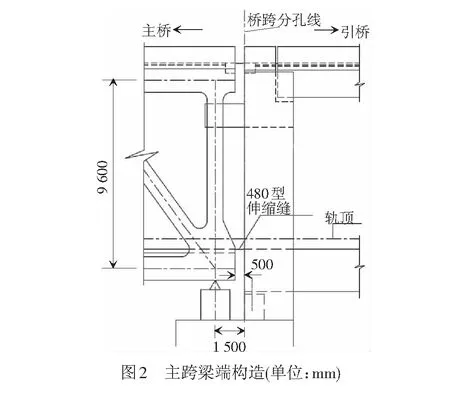
无砟轨道具有稳定性高、耐久性好、维修量少、结构高度小及自重轻等优点，因而被广泛运用于城轨桥，该桥原设计下层轨道结构即为承轨台式无砟轨道结构。然而，常规无砟轨道结构系统与桥梁处于较大的刚性连接状态[4]，对桥梁变位适应性较弱。计算结果表明，在设计荷载作用下，该大跨斜拉桥主跨梁端最大转角为3.86‰ rad，梁缝最大值为636 mm，而支座外侧悬臂长度达1 m，见图2，为典型的大转角、大梁缝与长悬臂结构，须在梁端敷设特殊轨道结构以保证轨道结构正常工作与列车走行性。

2 适应梁端变位的特殊轨道结构措施

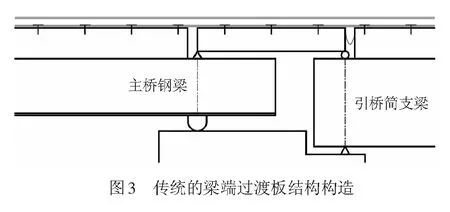
为适应梁端变位，德国提出在现有轨道结构上采用过渡板结构的措施，并在我国大跨度轨道桥梁建设中得到运用[11]。传统过渡板装置为简支结构，其支座位于桥梁支座正上方，在主桥上设置固定支座，引桥上设置活动支座，见图3。梁缝变化时，过渡板可沿线路纵向水平移动来调整；梁体转动时，过渡板可缓解梁端悬臂段上挑引起的钢轨“局部隆起”程度，从而改善钢轨和扣件受力。

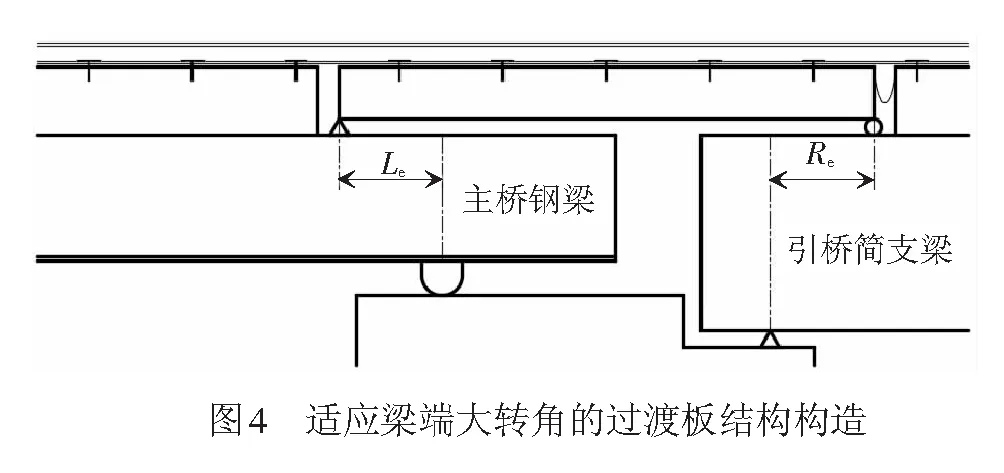
传统的过渡板结构将其支座与桥梁支座设计在同一竖直面上，虽然能有效缓解桥梁转动时悬臂上挑所致轨道结构不利受力，但对桥梁转动所致轨面折角的减小作用有限，当梁端转角较大时难以将扣件上拔力控制在安全范围内(见第4节计算结果)。为此，需在传统过渡板结构的基础上，将其支座内伸桥梁支座内侧以减小轨面折角，见图4。其中，Le为过渡板固定支座向主桥支座内伸长度；Re为过渡板活动支座往引桥支座内伸的长度，过渡板长度L=Le+1.9+Re(主桥支座至引桥支座的距离为1.9 m)，Le及Re的取值将在第4节阐述。

解决梁端变位过大的问题，还可以考虑铺设点支承的浮置式轨道结构。该类轨道结构一方面可跨梁缝设置；另一方面弹性较大，对桥梁变形有良好适应能力。本文采用的梯形轨枕轨道结构单元构造，每一单元梯形轨枕铺设在L型台座上，梯形轨枕长5.9 m，相邻单元纵缝10 cm(跨梁缝轨枕与相邻轨枕间纵缝增至15 cm以满足主跨梁端伸缩要求)，见图5。梯形轨枕纵梁采用C50混凝土预制，纵梁间设3道横向连接钢管。每一纵梁外侧设1处凸台以限制轨枕纵向位移，凸台与L型台座间设缓冲垫。纵梁底沿纵向每隔1.2 m设减振垫，共设5处减振垫，扣除减振垫自身宽度(25 cm)，相邻减振垫的净距仍约有1 m，可满足梁端大伸缩缝要求。

需要说明的是，理论上仅需在主跨梁端位置附近设梯形轨枕单元，而其余部位仍采用常规轨道结构即可适应梁端较大变位。然而，两种轨道结构刚度差异明显，若同时设于桥上将不利于行车，并将增加施工与养护难度。因此，下文讨论的梯形轨枕方案均指全桥铺设梯形轨枕情况。

3 梁端扣件受力计算方法及参数

梁缝两侧的主桥与引桥可能发生单侧转动也可能发生双侧转动，在每侧桥梁转动相同角度情况下，当桥梁悬臂长度较大时，单侧转动所致扣件受力最不利[4]。对于大跨度公轨两用桥而言，主桥梁端悬臂通常较长，梁端转角也明显大于引桥梁端转角，此外，主桥跨径往往大于列车编组长度，当主桥在列车荷载作用下发生最大转角变位时，引桥上并无列车加载。因此，可仅考虑主桥单侧转动情况分析大跨度公轨两用桥梁缝两侧梁体转动对扣件受力的影响。

在既有的公轨两用桥有限元模型基础上，建立梁端采用不同轨道结构的梁端扣件系统受力分析模型，见图6。扣件、减振垫及凸台缓冲垫均用弹簧模拟，钢轨、过渡板及梯形轨枕均用梁单元模拟，根据各构件的实际截面尺寸，采用刚臂单元模拟各构件中心的相对位置及位移关系，后续分析若无特别说明均指在桥梁主跨梁端发生3.86‰ rad转角情况下的扣件受力。自梁缝开始，左侧主桥上扣件编号分别为1′,2′,3′,…，右侧扣件编号分别为1,2,3,…。无砟轨道结构计算参数见表1，扣件受力分析目的在于控制其上拔力不超过WJ-2型小阻力扣件的初始扣压力。

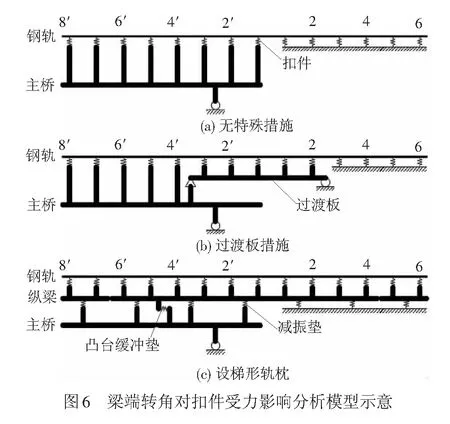
表1 无砟轨道结构计算参数

4 过渡板措施的扣件受力性能分析

梁端轨道结构采用1.9 m过渡板(过渡板支座位于桥梁支座正上方)与无特殊措施2种情况下，梁缝两侧扣件受力计算结果比较见图7。

由图7可知，无特殊措施时，受力最大的扣件位于离梁缝最近的位置，梁缝左侧主桥上1′号扣件承受最大下压力，梁缝右侧引桥上1号扣件承受最大上拔力，且远超限值(8 kN)。设置1.9 m过渡板后，1号扣件上拔力大幅减小，而梁缝左侧主桥上的扣件受力分布发生明显改变，1′号扣件由承受最大下压力变为承受最大上拔力，值为8.26 kN，稍超出限值；离过渡板端最近的3′号扣件由承受较大上拔力变为承受最大下压力；3′～7′号扣件上拔力均增大，其中，5′号扣件上拔力达7.38 kN。

计算结果表明，在大跨度桥梁端设置过渡板一方面可显著减小由于桥梁悬臂上挑导致的梁缝两侧扣件不利受力；但另一方面，过渡板本身为微型简支桥，当桥梁发生转动时，桥梁与过渡板形成相对转角，钢轨在过渡板左、右端出现轨面折角，导致过渡板端部扣件受力较大，梁端转角较大时扣件最大上拔力将超限。在主桥单侧转动情况下，过渡板两端的轨面折角θL与θR之和等于梁端转角θ，见图8。

显然，减小扣件受力的关键在于将θL与θR控制在合理域内。根据图8所示几何关系，若将过渡板支座往桥梁支座内侧延伸一定长度(Le与Re)，则θL随Le增大而减小，随Re增大而增大，θR则相反。扣件最大上拔力Fmax随过渡板固定支座向主桥支座内伸长度Le及过渡板活动支座向引桥支座内伸长度Re的变化规律, 见图9。

由图9可知，Fmax随Le增大而先减小后增大，Fmax随Re增大而先减小后增大又减小。其中，Fmax随Le变化规律出现锯齿形波动，是由过渡板端与过渡板上最外侧扣件相对位置的不同所致，当过渡板端与过渡板上最外侧扣件较近时(即扣件更靠近轨面折点位置)，扣件受力较大。

根据图9计算结果，比较典型Le与Re取值情况下扣件受力分布规律见图10，图10(a)中Re取0.0、1.8 m时，Fmax分别为8.26、7.96 kN；图10(b)中Re取0.0、1.8 m时，Fmax分别为7.37、6.44 kN；图10(c)中Re取0.0、1.8 m时，Fmax分别为4.23、4.93 kN；图10(d)中Re取0.0、1.8 m时，Fmax分别为5.55、4.27 kN。由图10可见，当Le与Re较小时(如Le=0.0 m，Le=0.6 m，Re=0.0 m)，θL较大而θR较小，增大Re则进一步增大θL而减小θR，过渡板左端扣件受力增大，但因为Le与Re较小时过渡板也较短，梁缝位置的钢轨曲率较大，导致该处扣件受最大上拔力，增大Re可减小梁缝处钢轨曲率，进而减小最大上拔力。当Le与Re取一定值时(如Le=2.4 m，Re=0.0 m)，θL与θR值相当，扣件受力几乎关于过渡板中心对称，且θL与θR所致扣件最大上拔力大于梁缝处钢轨曲率所致最大上拔力，此时，增大Le则增大θR，导致过渡板右端扣件受力最大，增大Re则增大θL，导致过渡板左端扣件受力最大。当Le较大而Re较小时(如Le=4.8 m，Re=0.0 m)，θL较小而θR较大，过渡板右端扣件受力最大，增大Re进一步增大θL而减小θR，扣件最大上拔力减小。

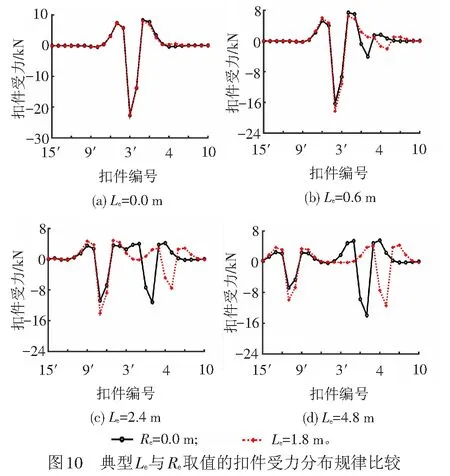
因此，对于大转角的大跨度桥梁，采用传统过渡板结构并不能有效减小梁端转角引起的过渡板端轨面折角，不足以将扣件受力控制在安全范围内，需将过渡板左、右支座往相应桥梁支座内侧延伸一定长度(Le与Re)以改善扣件受力。对于本桥，在梁端转角值3.86‰ rad情况下，建议取Le=1.2 m，Re=0.0 m(过渡板总长3.1 m，扣件最大上拔力6.83 kN)。对于类似桥梁更大梁端转角情况，可进一步优化Le与Re取值，计算结果见图9，Le与Re不同取值情况下，扣件最大上拔力的最小值为4.01 kN，即表明在轨道结构其他参数不变的前提下，将过渡板支座往桥梁支座内伸后，理论上可适应的梁端最大转角值约为7.7‰ rad。然而，过渡板作为微型简支桥，也应满足刚度要求，否则其将成为全桥薄弱环节而影响列车通行。相关规范[12]规定，设计静活载作用下，跨度30 m以内桥跨结构竖向挠度应小于l/2 000，据此得到不同跨度过渡板最小截面高度要求，见表2。

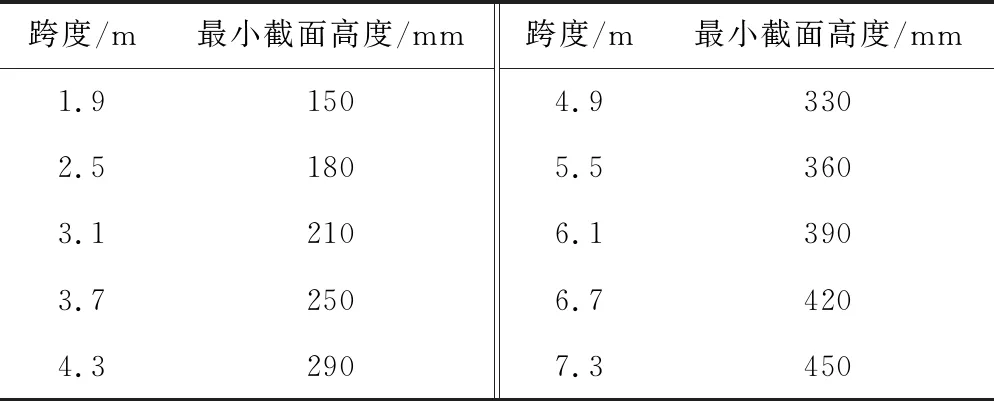
表2 满足刚度限值的不同跨度过渡板最小截面高度

根据表2计算结果可知，最小截面高度hmin基本随跨度l增加而线性增大，当l大于4.3 m后，hmin大于常规承轨台截面高度(300 mm)，即说明过渡板跨不宜超过4.3 m，否则，梁端以外的承轨台轨道结构高度也须随之增加，满足轨面标高要求，导致建筑高度与二期恒载加大，悖于桥梁结构合理设计。此外，考虑到过渡板底须预留一定高度(约50 mm)安装支座，过渡板截面高度不宜超过250 mm，得到过渡板跨不超过3.7 m。根据不同板跨的扣件最大上拔力计算结果，见图9，在限制过渡板跨不超过3.7 m的前提下，扣件上拔力最小值为4.93 kN(Le=1.8 m，Re=0.0 m时)，表明在其他参数不变的条件下，过渡板结构实际可适应的梁端最大转角6.3‰ rad。

5 梯形轨枕措施的扣件受力性能分析

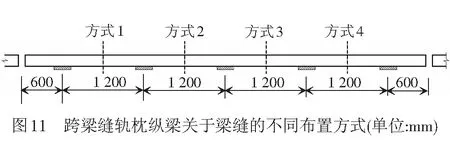
梁端铺设梯形轨枕轨道结构时，须将跨梁缝轨枕纵梁底某一减振垫设于主桥而将与之相邻的减振垫置于引桥。由图5可知，每一标准单元梯形轨枕纵梁底含5处减振垫，因此，若将相邻减振垫间隔中心与梁缝中心对齐，则跨梁缝轨枕纵梁共可能有4种布置方式，见图11，图中虚线表示梁缝中心位置。

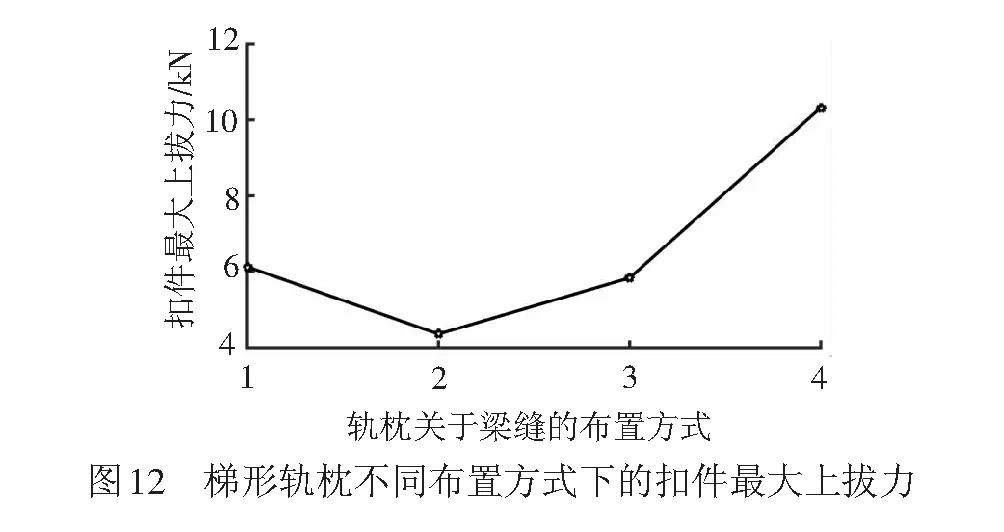
跨梁缝轨枕纵梁的不同布置方式下扣件最大上拔力Fmax计算结果见图12，可知布置方式对扣件受力有明显影响。方式1和方式3的Fmax在6.0 kN左右，方式4的Fmax最大，达10.32 kN，方式2的Fmax最小，仅有4.36 kN，与方式1(或方式3)相比也降低约27%。

按方式2铺设梯形轨枕后梁缝两侧的扣件受力计算结果见图13，图中还给出了等长过渡板方案的扣件受力分布情况。与等长过渡板方案相比，扣件最大上拔力减小29.7%。

由图13可知，铺设梯形轨枕后，梁缝位置及跨梁缝轨枕纵梁两端位置附近的扣件受力最为不利。紧靠梁缝的扣件受力较大是因为桥梁转动时该处轨道结构变形曲率最大，而紧靠轨枕纵梁两端的扣件受力较大是因为梯形轨枕为浮置式弹性轨道结构，当桥梁发生转动时，纵梁两端与相邻纵梁端部之间存在相对错位，进而导致扣件较大受力。可考虑在跨梁缝的轨枕纵梁两端增设减振垫以减小端部相对错位，跨梁缝轨枕纵梁两端是否设减振垫的扣件受力分布比较见图14，两端设减振垫后，最大上拔力为3.62 kN，与两端未设减振垫情况相比降低17%。

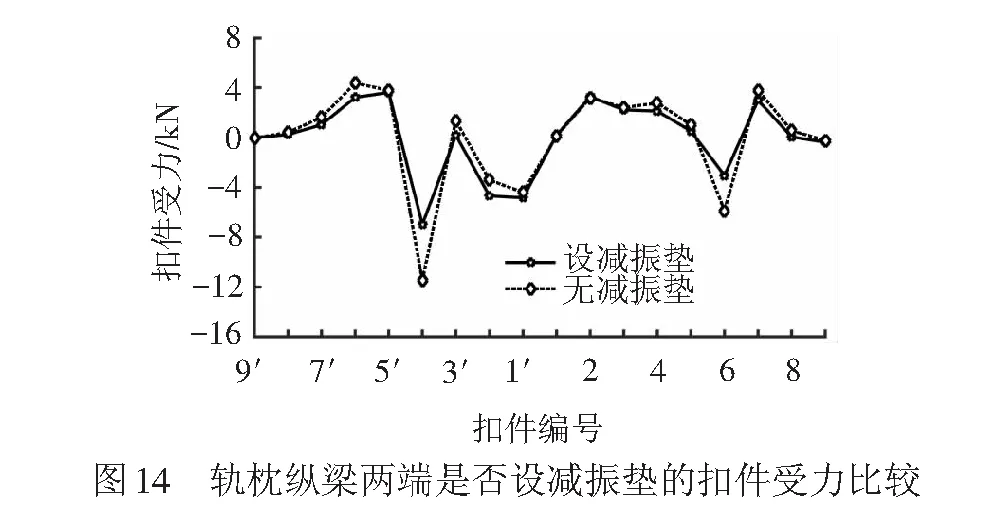
实际运营过程中，在外部自然环境和列车往复荷载作用下，梯形轨枕减振垫将不可避免地发生老化，减振垫刚度都将随时间推移而增大。在轨枕纵梁两端设与未设减振垫两种情况下(均按方式2布置)，扣件最大上拔力随减振垫刚度增加的变化规律见图15。由图15可知，扣件最大上拔力随减振垫增加而增大，说明减振垫刚度的增加降低了轨道结构弹性，使得轨道结构与桥梁处于更大刚度的连接状态，进而使扣件系统对桥梁变位的反应更为敏感。

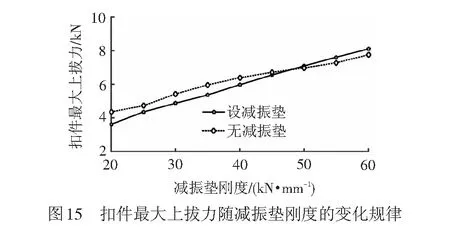
由图15可知，减振垫刚度Kj增至约50 kN/mm时，轨枕纵梁两端设与未设减振垫所致的扣件最大上拔力几乎相等；Kj不超过50 kN/mm时，轨枕纵梁两端设减振垫更有利于减小扣件最大上拔力，而Kj超过50 kN/mm后，轨枕纵梁两端不设减振垫更有利。说明当Kj达50 kN/mm后，轨枕纵梁两端再增设减振垫不仅不能有效减小纵梁端部之间相对错位，反而降低了轨道结构弹性，不利于扣件受力。但即便Kj增至原设计值(20 kN/mm)的2.5倍(50 kN/mm)，扣件最大上拔力(7 kN)也未超出限值(8 kN)，表明梯形轨枕可显著改善大转角、长悬臂情况下的扣件受力并具有良好适应性。

前述过渡板为简支结构，不同的是梯形轨枕为多跨连续梁结构，其在每一减振垫处为弹性支撑，桥梁转动相当于在轨枕纵梁底施加不均匀的基础位移，从而导致扣件受力。在给定桥梁梁端转角情况下，梯形轨枕基底位移由每一减振垫是否在桥上及其与桥支座的相对位置决定。桥梁的悬臂长度Lc一旦确定，梯形轨枕的基底位移取决于桥梁梁端与跨梁缝轨枕纵梁端部(取左端)的距离ds，见图16。

保持轨道结构参数不变，令桥梁梁端发生单位转角(1‰ rad)，计算轨枕纵梁两端设与未设减振垫两种方式的扣件最大上拔力随Lc与ds值变化规律，见图17。在桥梁参数(Lc)确定的情况下，桥梁梁端与跨梁缝轨枕纵梁端部的相对位置(即ds)的不同导致扣件受力存在差别，可通过调整ds值来使扣件受力最小(即使可适应的梁端转角最大)。不同Lc取值条件下轨枕纵梁两端设与未设减振垫两种方式可适应的最大梁端转角[θmax]及相应的最佳ds值见表3。

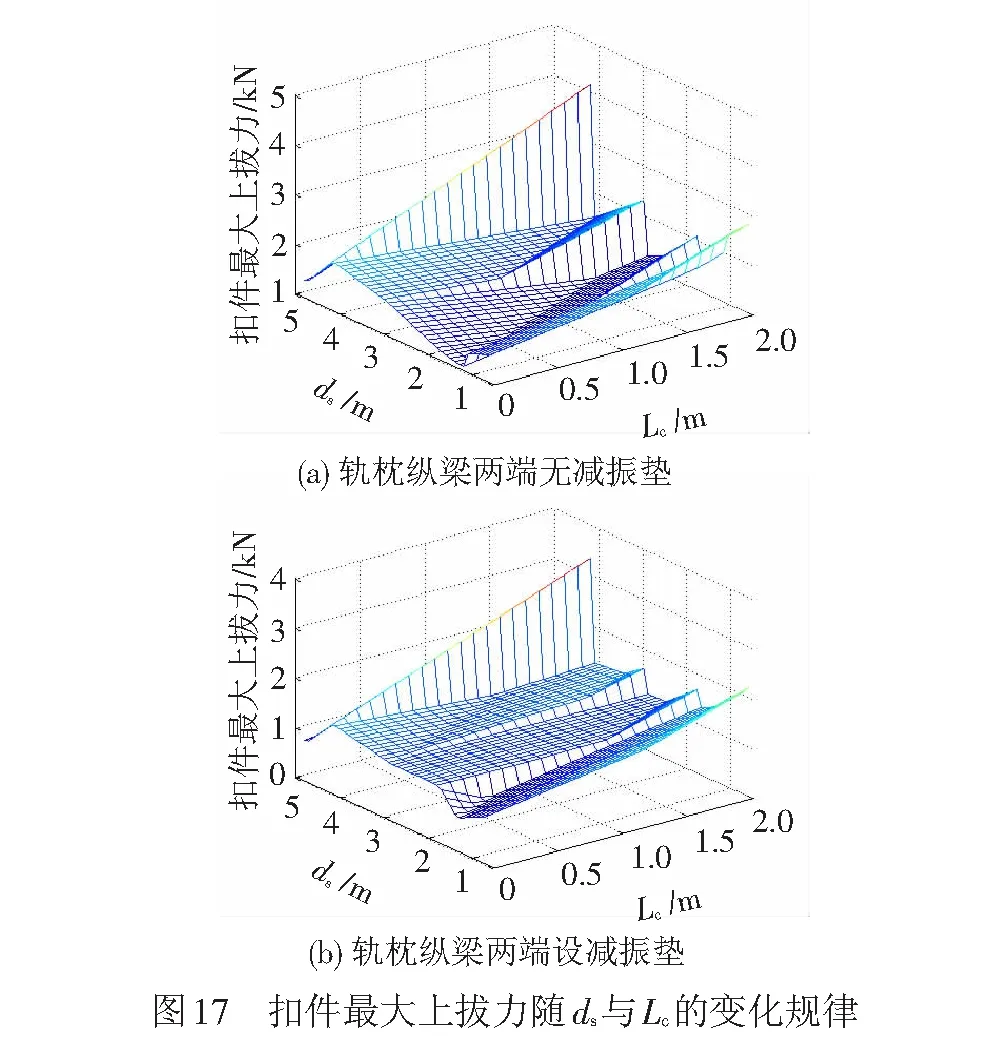
表3 梯形轨枕可适应的梁端最大转角及相应布置

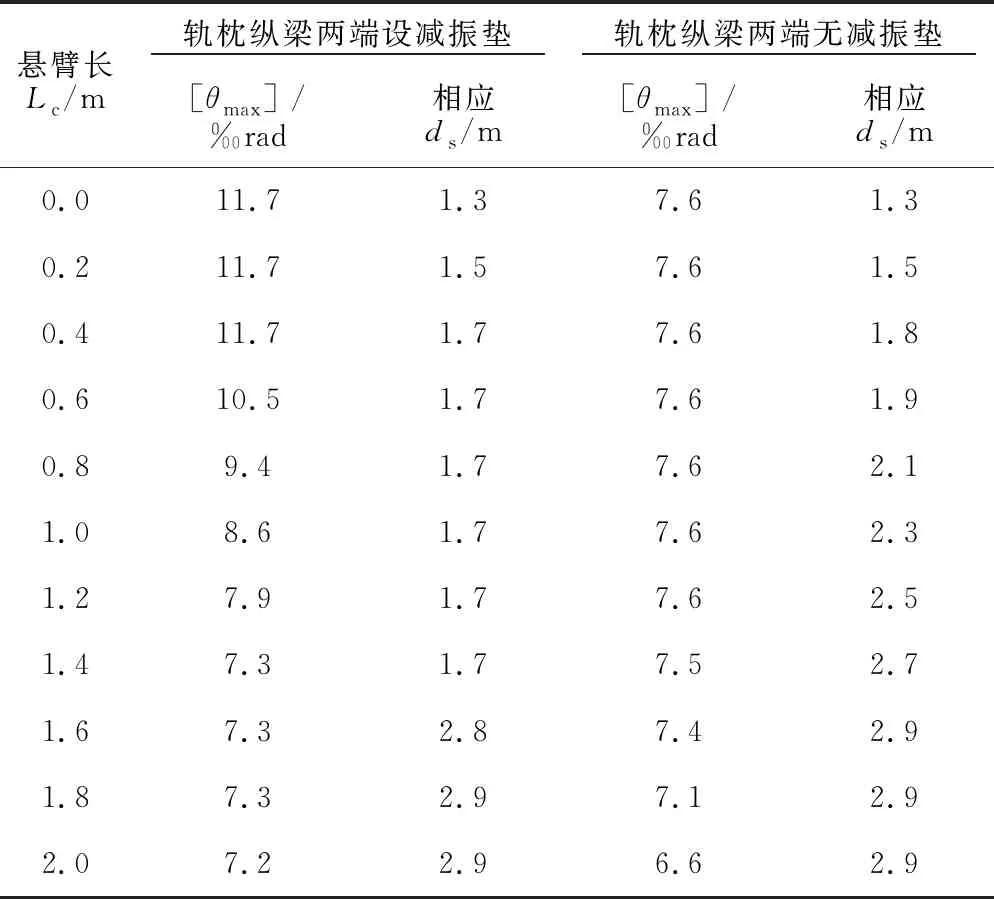
悬臂长Lc /m 轨枕纵梁两端设减振垫轨枕纵梁两端无减振垫 [θmax] /‰rad相应ds /m[θmax] /‰rad相应ds /m0.011.71.37.61.30.211.71.57.61.50.411.71.77.61.80.610.51.77.61.90.89.41.77.62.11.08.61.77.62.31.27.91.77.62.51.47.31.77.52.71.67.32.87.42.91.87.32.97.12.92.07.22.96.62.9

由表3可知，桥梁悬臂长度Lc越大，梯形轨枕可适应的最大梁端转角[θmax]越小，Lc值达2.0 m时，梯形轨枕仍至少可适应6.6‰ rad的梁端转角，而在轨枕纵梁两端设减振垫可进一步增强梯形轨枕对梁端转角的适应性。在类似轨道桥梁的设计与施工中，可根据桥梁梁端转角大小及悬臂设计长度，参考表3确定在梁端采用梯形轨枕措施的可行性，铺设梯形轨枕时还可参考表中结果确定轨枕纵梁至桥梁梁端最佳相对位置以及是否有必要在轨枕纵梁两端增设减振垫。需要说明的是，表3结果是基于表1所列轨道结构参数计算得到的，当轨道结构参数变化时，可采用类似方法具体分析。