基于广义随机Petri网的铁路四电工程建设全过程质量控制研究
2019-12-02徐建军
徐建军, 卢 睿
(1. 川藏铁路有限公司, 四川 成都 610043; 2. 中铁武汉电气化局集团有限公司, 湖北 武汉 430074)
作为电气化铁路的重要组成部分,铁路四电系统是电气化铁路具有强大动力以及安全高效调度的重要保障[1]。铁路四电工程集成度和复杂性高,涉及部门多,一旦发生质量问题将造成极大的财产损失和安全事故。为避免铁路四电系统运营质量问题,必须从项目建设源头出发,对项目建设的不同阶段、不同环节进行全过程的监督管控。
铁路四电工程具有显著的单件性特点,每个分项工程都各不相同,在工程质量管理上表现出不同的质量控制目标和约束因素[2]。相关研究表明,铁路四电工程的质量管理研究明显滞后于站前工程,而且铁路四电工程质量管理的研究重点在施工阶段,对全生命周期质量控制流程的建模与性能分析较少。铁路四电工程质量管理相关研究的科学性、系统性不足,造成了四电工程项目质量管理系统不清、重点不明、流程不顺、沟通不畅,极大影响了四电工程项目各参建企业整体质量管理效能的发挥。铁路四电工程项目的建设全过程主要包括前期规划与设计、物资采购与施工、质量验收与交付3个阶段,各阶段之间相互关联、缺一不可。不同阶段以及各参与主体之间存在大量的信息传递、储存和处理过程。因此,铁路四电工程项目的质量信息来源于全生命周期的各阶段,在进行质量控制研究中应采用生命周期理论将阶段分析和整体把握相结合,而不仅仅注重于某一阶段的质量控制工作。
质量控制过程建模是从“过程”视角,对复杂质量控制过程的结构与关系进行抽象化表达,通过建立质量控制过程的结构化模型元素及规范,优化质量控制过程,进而提高质量管理能力[3]。Petri网是一种适合描述工作流过程的数学建模方法,适用于描述与分析离散时间动态系统[4]。铁路四电工程质量控制流程是一个离散的时间动态系统,其建设全过程的各个阶段以及子过程组成的逻辑关系可以看成广义的工作流。因此,Petri网可用于铁路四电工程建设全过程质量控制过程的系统建模。
王孟钧等[5]、韩宇[6]和张柏煌[7]等诸多学者对铁路建设项目质量控制建模方法和模式进行了一定的研究,李倩等[8]从绩效评价的角度对高速铁路建设的质量管理进行了分析,但目前还缺乏对四电工程建设全过程质量管理模型的探索。本文引入Petri网对该过程进行建模和仿真:首先,建立铁路四电工程项目建设全过程质量控制过程体系;其次,根据质量控制全过程的各个阶段以及子过程组成的逻辑关系,选用广义随机Petri网对铁路四电工程建设全过程质量控制过程进行标准化建模,并对建立的质量控制模型进行有效性验证。最后,在标识稳定概率的基础上,从时间维度下明确铁路四电建设全过程质量水平的计算方法。
1 铁路四电工程项目建设全过程质量控制特点分析
相比于铁路站前工程,四电工程是一项专业性和综合性极强的系统工程。其建设全过程质量控制工作主要存在以下特点:
(1) 质量控制面广
铁路四电工程项目质量控制管理涵盖项目前期规划到后期运维全生命过程,每个过程又涉及人员、设备、管理和环境等因素,因此项目全生命周期内质量控制程序繁杂,涉及专业面广泛。
(2) 质量影响因素多
铁路四电工程项目涉及专业多,周期长且通常在野外进行施工作业,存在各种各样的质量影响因素。任何一个方面考虑不周全,都会导致四电项目出现质量问题。
(3) 质量水平波动大
铁路四电工程项目对工作人员的设备安装稳定性要求大。受野外环境影响,四电工程项目作业过程中还存在大量不可预测的影响因素,因此工程质量存在较大的波动性。
(4) 风险隐蔽性强
铁路隧道内四电工程线缆和设备布设密集,隐蔽工程多,质量问题和风险不易发现。另外站区地下综合管线排布复杂,容易产生空间冲突。
(5) 质量评定难
目前铁路四电工程项目各专业质量验收标准独立,缺乏统一协调的质量验收和评定标准。各专业之间的接口质量问题、站前与站后工程衔接质量问题评定较困难。
2 基于Petri网的铁路四电工程建设全过程质量控制流程建模
2.1 工程建设中的质量与工期关系分析
工程项目的质量取决于一系列相互关联、相互制约的工序质量。同时,工序的质量与工期(即持续时间)密切相关。合理的工期对应合格的工序质量,不同的工期会形成不同的工序质量,每项工序质量的好坏将直接影响整个工程质量。相关研究表明[9-10],随着时间的持续增加,工序质量快速提升,到达正常持续时间后,由于边际效用的存在,即使继续增加时间,工序质量也不会有明显提高,甚至会下降,其函数图像与二次函数比较吻合,见图1。
图1中,Q为质量水平,表示工序质量满足要求的程度,Q∈[0,1],Q越接近0质量水平越低,越接近1质量水平越高;T*为最佳工期目标,此工期是在费用最低,且可以保证铁路四电工程项目质量目标的前提下确定的;Ta为最短工序工期,即满足最低质量要求的工期;Tb为临界工期。实践证明,当T*

根据质量水平-工序时间关系图,建立工序质量控制模型为
Qi=Aiti2+Biti+Ci
( 1 )
式中:Qi为质量控制工序i对应的质量控制水平指数;ti为质量控制工序i的工期;Ai、Bi和Ci为工序质量控制模型的系数。基于此模型,可明确不同工期下的项目质量水平。
2.2 基于Petri网的LQC模型构建
Petri网是从过程的角度出发,为复杂系统的描述与分析提供的一种有效建模工具。通过多元组合而成的网状结构,Petri网能表达出并发、冲突、同步、资源争用等系统过程,并且将复杂系统的结构和业务流程进行可视化,具有图形建模方法的优点,而托肯在网中的流动又可以准确地表达出系统的动态行为。
本文从全生命周期的视角,通过将铁路四电工程项目建设全过程中的质量控制工序的逻辑关系看成广义的工作流,应用Petri网对这些逻辑关系进行梳理,建立基于Petri网的铁路四电工程项目建设全过程质量控制LQC(Lifecycle Quality Control)模型,实现对铁路四电工程全过程质量的有效控制。
定义基本Petri网为一个四元组
W=(P,T,F,M0)
( 2 )
式中:P={P1,P2,…,Pm}为W有限库所集合;T={T1,T2,…,Tn}为W的有限变迁集合;F⊆(P×T)∪(T×P)为流关系(即有向弧集);M0:P→{0,1,2,…,N}为初始标识,M0={u1,u2,…,um},uj为库所Pj处的托肯数,j=1,2,…,m,托肯在不同库所的数目代表了系统的不同状态。P与T的关系可以表示为P∩T= Ø且P∪T≠Ø。
基于现有研究以及对铁路四电工程参建企业的调查和访谈,从全生命周期角度,提炼出各阶段的质量控制要点,形成完整的铁路四电工程项目建设全过程质量控制流程,见图2。
在图2的基础上,运用GSPN(Generalized Stochastic Petri Nets)理论,对铁路四电工程项目全生命周期质量控制流程进行层次化建模,建立铁路四电工程项目全生命周期质量控制模型即LQC模型见图3。



表1 库所定义

库所Pj定义库所Pj定义P0铁路四电工程建设项目立项P15有质量问题的接口P1四电工程项目接口设计完成P16有质量问题的材料和设备P2四电工程基础接口施工阶段P17进场施工准备阶段P3完成四电质量控制计划P18施工测量误差校准完成P4完成物资招标技术规格书编制P19四电施工、设备安装质量检查完成P5完成四电施工图纸设计P20四电施工和设备安装质量问题P6技术规格书审核通过P21设计因素引起四电质量问题P7四电施工图纸设计通过审核P22准备接受四电静态调试P8准备四电工程施工和物资招标P23四电静态调试完成P9选定四电施工单位P24四电静态调试问题整改完成P10选定四电物资供应单位P25完成四电工程竣工验收质量评定P11接口检查准备工作完成P26完成联调联试P12确定四电项目各种材料和设备型号P27联调联试问题整改完毕P13接口检查完成P28质量文件整理完毕、投入运营P14完成材料质量检测

表2 变迁定义
2.3 模型有效性检验
对建立的LQC模型进行有效性检验是进行系统质量水平分析的前提。可根据Petri网理论按照不变量计算结果来判断建立的LQC模型是否有效,即是否具有有界性和活性。不变量是Petri网的结构性质,包括S-不变量和T-不变量,S-不变量和T-不变量具有完全相同的性质。本文采用T-不变量来检验铁路四电项目LQC模型的有效性。
设Petri网N=(P,T,F),|P|=m和|T|=n分别表示库所和变迁个数,Am×n为N的关联矩阵。根据T-不变量的定义和建立的铁路四电工程建设全过程质量控制LQC模型,可得到T-不变量集合为
( 3 )
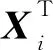
由于T-不变量的定义同样满足Petri网结构有界性的判定定理,即存在非平凡的非负整数向量X,使得AX≤0可知,该模型具有有界性。综上,本文提出的铁路四电工程建设全过程质量控制LQC模型有效。
3 LQC模型性能分析
通常GSPN模型中包含了若干个瞬时变迁和时间变迁,根据GSPN理论定义,仅使时间变迁可实施的状态为实存质量状态(Tangible),而使瞬时变迁可实施的状态为消失质量状态(Vanishing)。根据LQC模型同步构建的GSPN模型可达图见图4。

由消失质量状态构成的消失质量状态集为Svan={S20,S25,S27,S30,S31,S38,S39,S40,S41,S47,S56},其余46个均属于实存质量状态集合Stan。
已经证明,GSPN的可达图同构于一个齐次有穷状态和连续时间的嵌入马尔可夫链(Embedded Markov Chain,EMC)[12-13]。因此可以利用EMC求解GSPN模型的稳态概率。其基本思路是在嵌入的马尔可夫链EMC中移去消失质量状态,仅在压缩的EMC即REMC(Reduced Embedded Markov Chain)上计算实存质量状态之间的转移概率。
3.1 标识稳定概率求解


( 4 )
式中:E(Sd)为实存质量状态下可实施的变迁集;Tk为变迁集中的一个个体。
3.2 时间维度下的铁路四电工程全过程质量分析
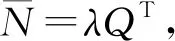
( 5 )
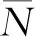

( 6 )
本文中,对于∀pj∈P,∀d∈N,P[S(pj)=d]表示库所pj中包含d个托肯的概率,其中Sj为初始标识S0的可达状态记作Si∈[S0]且Sj包含元素pi。从标识的稳定概率求得库所Pj的托肯概率密度函数为
( 7 )

( 8 )
4 算例


表3 铁路四电工程项目LQC模型的变迁激发速率
4.1 平均托肯数
根据统计数据计算得到铁路四电工程项目LQC模型稳定质量状态概率,进而得到各库所的平均托肯数,见表4。

表4 铁路四电工程项目LQC模型平均托肯数
由表4可知,库所P19接口质量检查结束、P23四电设备施工安装质量问题整改和P26静态验收克缺问题调整3个阶段的平均托肯数较小,表明此3个环节工序持续时间较长,质量控制水平较低,因此更容易成为铁路四电项目建设全过程中的质量控制瓶颈环节。相关部门在进行四电工程建设时应将这3个环节作为质量管控优化的重点。
4.2 变迁利用率

表5 变迁利用率
4.3 某新建铁路四电工程全过程质量控制水平分析
根据得到的库所平均托肯数和变迁利用率,结合系统平均质量水平计算公式,可得到该新建铁路整个四电工程项目建设全过程质量控制的平均水平。
即该新建铁路整个四电工程的平均工程质量控制水平指数为0.923 8,远大于0.7,表明该新建铁路质量控制流程和方案满足要求四电工程质量目标要求。
基于工序质量和工序时间的量化关系,本文建立的铁路四电工程建设全过程质量控制LQC模型通过建立全过程质量控制Petri网和GSPN可达状态图,重点考虑了各阶段和各质量控制工序之间的联系。因此得到的项目建设全过程质量控制水平分析结果具有一定的客观性,在一定程度上优于传统工程质量的加权系数法和模糊评价方法。
5 结束语
铁路四电工程项目建设全过程质量控制中构建的LQC层次化模型,在GSPN可达图的基础上建立了同构于连续时间的嵌入马尔可夫链EMC,并利用REMC对铁路四电工程项目LQC模型质量控制水平进行分析。可以有效地识别建设全过程中质量管控的瓶颈环节,同时全面地分析整个铁路四电项目建设全过程质量控制水平。以库所平均托肯数、变迁利用率、平均质量控住水平为质量分析指标,分别从状态、变迁和时间角度得到的铁路四电工程全过程质量控制水平结果更为可靠,达到能量化分析瓶颈环节和关键节点对全过程质量控制水平的影响,对实现铁路四电工程项目质量控制过程的协同管理和信息化管理具有重要意义。
