高速列车等效通过时间预测

郭 磊， 葛剑敏

(同济大学 物理科学与工程学院， 上海 200092)

高速列车作为重要的公共出行方式在人们生活中扮演着越来越重要的作用，但同时铁路沿线的居民却受到列车经过时通过噪声的困扰.随着列车速度的进一步提高，铁路噪声的预测和降低在世界范围内引起越来越多的重视.高速列车产生的噪声可以通过观察点声压级随时间变化曲线表示，通过噪声曲线提供了大量的列车噪声信息，因此分析通过噪声可以更好地了解列车经过过程中噪声的产生机理，验证运动声源辐射公式，分离无法直接测量的声学参数，如源强和声源指向性等.早期铁路噪声预测都以轮轨为主要噪声源，各国相继提出符合本国列车噪声特性的铁路噪声预测模型[1-2].焦大化[3]在大量试验的基础上，结合理论分析与数据对比，提出时速71 km·h-1货车通过噪声预测模型，并在此基础上研究低速下列车运行噪声的等效通过时间计算方法.

当列车速度进一步提升，尤其是在研究300 km·h-1及以上高速列车时，列车运行的动态环境以气动作用为主[4]，气动噪声将取代其他噪声作为主要噪声源.本文基于气动声学研究高速列车声传播模型，分析300 km·h-1及以上高速列车不同声源的声学特性，提出适用于高速列车的通过噪声预测模型，并将其运用在列车噪声等效通过时间的计算中，为新建中高速铁路噪声预测和环境评价提供依据.

1 高速列车等效通过时间

铁路噪声预测方法主要采用模式预测法和比例预测法两种.比例预测法使用条件限制严格，仅可应用于工程前后环境变化不大的工程项目.对于新建项目和变动较大的改建项目，应采用模式预测法.随着预测技术的不断发展，依据铁计[2010]44号文件,目前使用的铁路噪声等效声级LAeq,p预测公式为

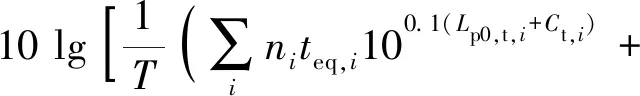
(1)

式中：T为规定的评价时间；ni为时间T内通过的第i类列车列数；teq,i为第i列车通过的等效时间；tf,i为固定声源的作用时间；Lp0,t,i、Lp0,f,i为源强；Ct,i、Cf,i为修正项.

高速列车等效通过时间计算是铁路噪声预测的重要环节，涉及列车声源分析、源强计算、声传播分析等，车速与距离的变化对其也有较大影响，精确计算等效通过时间可以提高铁路噪声评价的准确性.将高速列车等效通过时间teq作如下定义：记列车中部通过时受声点的声压为pm，若一稳态噪声以pm作用一段时间teq与列车通过时噪声辐射的总能量相等，则称teq为等效通过时间.根据定义，有

(2)

式中:p(t)为瞬时声压；p0为基准声压，p0=20 μPa.

可导出

(3)

这是计算等效通过时间teq所依据的原理性公式.记列车中部通过观察点时刻为0，则pm=p(t=0).因此，只要知道观察点通过噪声随时间的变化情况，就能准确计算等效通过时间.

传统通过噪声预测模式[3]由声传播理论得出观察点声压公式，对有限长线声源，受声点的瞬时声压p(t)2的微分表达式为

(4)

式中：I0为单位长度声源的参考距离声强；ρ为空气密度；c为声速；r0为参考距离；r为声源与受声点距离；cosnθ为指向性因子.

式(4)在列车长度l上的积分为

(5)

式中：d为受声点到声源所在平面的水平距离.

(6)

式(6)由点源公式推导得到，其考虑了不同位置点源声传播路径的差异，但没有考虑声传播和接收的时间也不相同.铁路噪声测试标准ISO 3095—2013[5]中规定，观察点距离轨道中心线25 m，不考虑高差影响.当列车中部正好通过观察点断面时，高速列车中部声源距离观察点25 m，声传播时间小于0.1 s .16节编组列车全长约400 m，列车头部声源传播到受声点的时间约0.7 s.很显然由时间延迟造成的误差不能忽略，当观察点位置移动时这种时间延迟效应也相应改变.

2 高速列车等效通过时间预测模型

2.1 声源分析

列车车外噪声随着车速的变化呈现不同的特性，随着声学理论与测量技术的不断进步，高速列车声源识别与声场分析已有大量研究成果[6-8]. 250 km·h-1及以上高速列车车外噪声中滚动噪声和气动噪声起绝对主导作用[9].在研究300～380 km·h-1高速列车时，气动噪声将取代其他噪声作为主要噪声源.

Ffowcs Williams-Hawkings方程(简称FW-H方程)描述了任意运动固体边界影响产生的流动发声问题.对于正常行驶的高速车辆，车体结构坚固，车身表面体积脉动量趋近于零，也即FW-H方程中单极子声源项较偶极子声源项小，可忽略不计.又根据Lighthill理论：流场中四极子声源与偶极子声源强度之比Equa/Edi正比于马赫数的平方[10]，而高速列车的运行速度仍处于低马赫数(以本文考虑车速上限380 km·h-1计算，其Equa/Edi=0.096)，此时高速列车表面气动噪声中四级子声源的影响可忽略不计.FW-H方程可作如下简化[11]：

(7)

可见，高速列车外部噪声声源类型复杂并以偶极子噪声为主，车辆表面偶极子声源的分布规律和声传播特性决定着高速列车通过噪声的变化情况.由此，本文在理论推导时声源指向性采用以偶极子为主的cosθ，并对整体指向性因子附加指数参数n(0 ≤n≤ 2 )，通过与试验数据的对比优化指向性参数.

2.2 等效通过时间预测模型

高速列车外部噪声无论是看作线声源还是点声源，都可以认为是由系列点源组成.因此，通过分析运动点源的声传播模型可以很快地建立高速列车声传播模型.

在通过噪声预测时，建立相对地面静止和随车匀速运动的两个坐标系，分别描述声场和声源信息，它们之间的关系如图1所示.声源的外表面固定在y=y0平面上，平面沿x正方向以速度v匀速运动.观察点K相对地面静止位于oyz平面内，在t=0时刻列车中点通过观察点.局部运动坐标系Oαβ以轨面和列车中心线交点为原点并以速度v随列车同步移动，Oαβ坐标原点O在全局坐标系中的坐标为(x0,y0,z0).

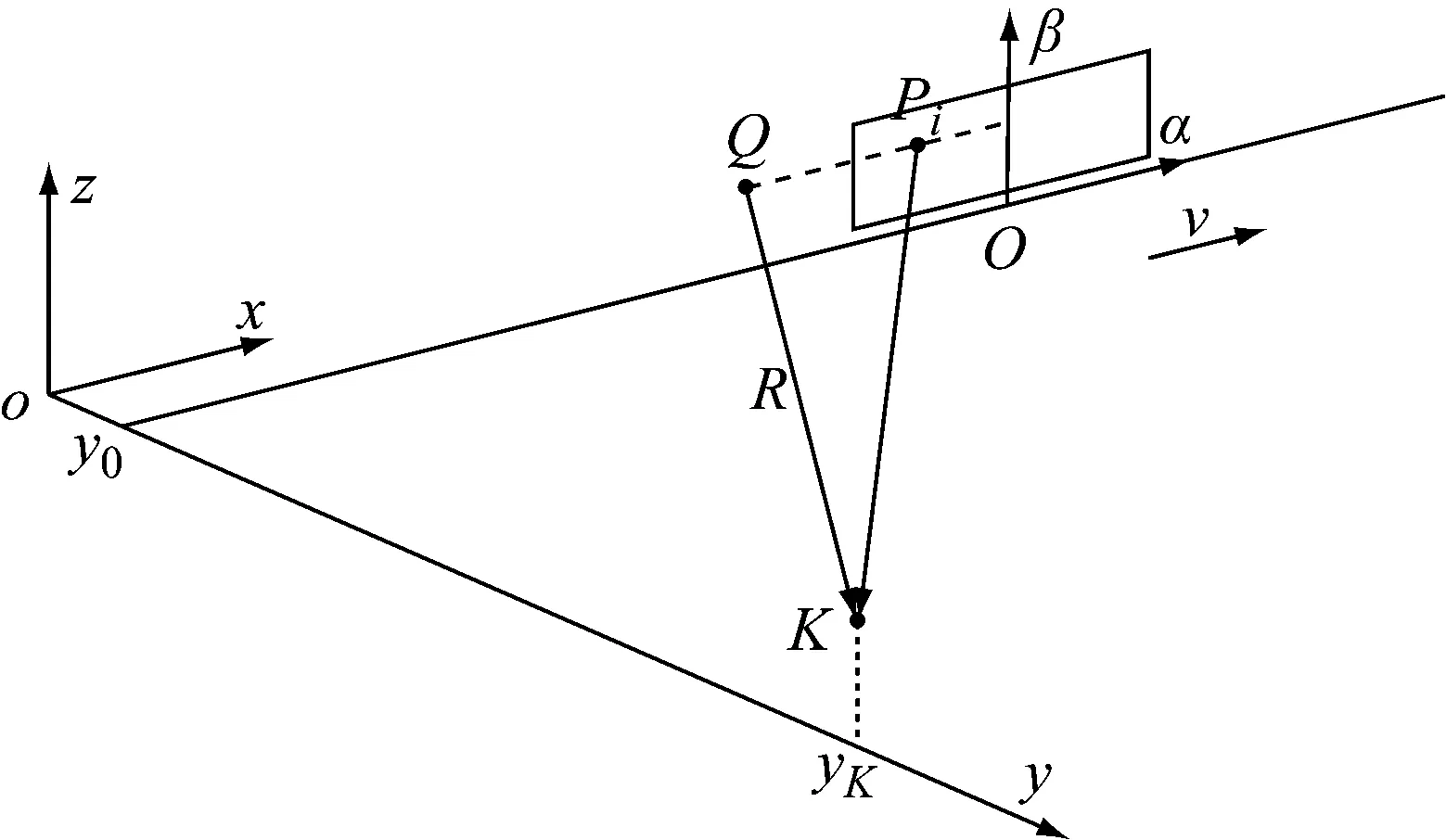
图1 高速列车通过噪声预测模型示意图

在列车平面内，取任一噪声源Pi，其在Oαβ内的坐标为(αi,βi).在t时刻，观察点K(xK,yK,zK)接收到的声压是声源Pi在τ=t-RiK/c时刻由Q点发出的.记R为QK的距离，则

(8)

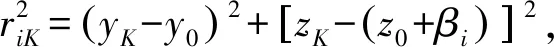
(9)

引入

(10)

式中：马赫数M=v/c.对于高速列车，M<1，式(9)应取正号，由此建立声源场与声辐射场的时空关系.定义由空间声传播引起的时间延迟函数Δτ(t)为

(11)

t时刻P点与观察点连线与z轴正方向的夹角记为φ，在此模型中-8°<φ< 4°，且对任一点声源，在通过观察点的整个过程中，其水平方向角始终保持不变，因此本文不考虑垂直指向性的影响.记t时刻列车运动方向与R的水平夹角为θ，可以推出

(12)

以速度v沿x正方向运动的理想偶极子源所产生的声压波动方程为

(13)

在亚音速运动中

(14)

力分量为fi(0,f2, 0)的横向偶极子的声压场可以表示为

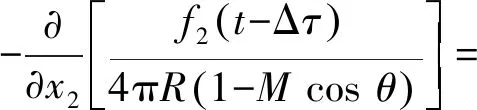
(15)

从式(14)和(15)中可以看出，观察点测得的压力由声源的特性函数随时间的延迟和振幅的衰减决定，时间延迟函数和振幅变化系数都随时间而变化.令

(16)

对于高速列车，其主要噪声源为偶极子引起的气动噪声，同时也有单级子及四级子噪声的影响.因此，对任意质量源为qi的点源，受声点的声压级公式作如下假设:

(17)

0 ≤n≤ 2.

因此在t时刻观察点K接收到的声压与声源Pi的关系可以表示为

(18)

对任意类型声源，记其在列车平面内的分布为S(α,β)，观察点K在t时刻接收到的总声压pK(t)是由列车平面内不同位置处的点源在不同时刻历经不同时间延迟后叠加的结果，则在任意时刻t观察点K接收到的总声压表示为

(19)

代入式(3)得

(20)

实际计算时，观察点t时刻接收到的声压是由系列点源在不同时刻发出的，pk(t)难以直接获得.本文在计算时将时间离散化，系列点源分别单独通过观察点，再以Δt为时间间隔，将在每Δt内传播到观察点的噪声进行叠加，最终绘制叠加后的声压级曲线.当Δt的取值使得前、后两次观察点计算的结果偏差小于0.1 dB时，取满足条件的最大Δt作为时间间隔，所得曲线即为较准确的通过噪声预测结果.利用MATLAB软件实现上述过程并绘制通过噪声曲线.

3 试验验证与分析

3.1 高速铁路噪声试验

高速铁路噪声特性研究是预测高速列车等效通过时间的基础.为掌握高速铁路噪声源特性及声传播规律，采用PLUSE Labshop多通道声学测量系统在京沪高速铁路上对高速列车运行状态下的空间声场进行现场测试.进行测试的动车组列车为我国CRH380AL型16编组高速列车，速度范围为300～380 km·h-1，列车和线路状况满足ISO 3095—2013标准[5].

如图2所示，在距离轨道中心25 m、轨面以上3.5 m处布置传声器，当列车距离测试点2 km时开始测量，单次测量时间为2 min，单通道采样频率设置为25.6 kHz.

图2 高速列车通过噪声测点示意图(单位:mm)

高速列车以300、350、380 km·h-1匀速通过时所测观察点K声压级SPL (sound pressure level)的时间历程如图3所示.可以看出，随着列车接近观察点，SPL曲线迅速增加；列车通过时，声压级曲线保持在较高的水平；当尾车驶离时，声压级曲线逐渐下降到初始值.由式(11)可知，在距离观察点相当远的地方，列车不同部位产生的声音时间延迟函数Δτ(t)较大，当列车靠近时Δτ(t)逐渐变小，列车远离时Δτ(t)逐渐变大.因此在列车驶近时，在相同时间间隔内离散化计算模型将捕获更多的声信号，当列车远离时则相反，这导致声压级的增长速度明显快于其下降速度，即曲线的形状是一个不对称的梯形.当车速提高时通过噪声曲线顶部逐渐出现两个明显的凸起.

图3 300、350、380 km·h-1高速列车通过噪声曲线

声源特性和声传递关系是决定高速列车通过噪声的重要因素，为了准确描述观察点的声压，国内外从这两个方面展开了大量的研究[1]，提出基于本国铁路噪声的各种假设.模型中的声功率级大多以辐射值的形式给出，并对列车的数量、速度、轨道的类型以及桥梁进行修正.如图4所示，在CRH380AL型高速列车外部不同区域布置平面传声器采集噪声数据，根据测量结果将声源等效为3部分：列车底部线声源、中部线声源和顶部点声源.基于试验数据对车底部和车中部单位长度线声源声功率级、受电弓点源声功率级进行试计算幅值，然后计算列车通过过程中观察点的通过噪声曲线，以0.1 s为时间间隔计算其与实测值的标准差，利用最小二乘法求得满足上述条件的最优解.声源位置信息及参考源强值见表1.

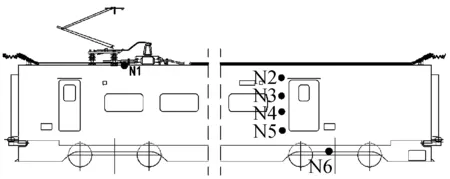
•噪声测点

3.2 模型验证与优化

利用表1声源数据计算CRH380AL型高速列车300～380 km·h-1速度下通过噪声曲线，并与实测曲线进行比较.300 km·h-1通过噪声曲线对比如图5所示.

由图5可知，预测曲线在列车通过时段内与实测结果有较好的一致性，受电弓通过时刻预测曲线有明显突起.在列车驶近和远离的过程中，预测值较实测值偏小.相关研究表明[11]，通过噪声的曲率与声源指向性有关，因此对式(17)中的指向性参数n进行优化.引入差值分析参数S

表1 不同速度下CRH380AL型高速列车声源信息

图5 300 km·h-1、距离25 m时实测与预测数据对比

(21)

式中：pc,i为仿真预测值；pm,i为试验测量值.在列车通过的整个阶段，将预测值和试验测量值每隔0.1 s在同一通过噪声时间历程中绘制出来，改变指向性参数n，使差值分析参数S取最小值.当n=0.85时，时速300 km·h-1高速列车通过噪声预测结果最优，S=0.89 dB(A)，优化曲线见图6.

将指向性参数修正为n=0.85，代入其他车速下的预测程序，预测曲线表现出良好的一致性. 350 km·h-1和380 km·h-1高速列车通过噪声预测与实测曲线如图7所示.

以上预测数据与实测结果吻合很好，其方法可以用于预测更多速度及距离下列车的通过噪声.按式(3)与式(20)分别计算25 m处不同速度下观察点实测与预测等效通过时间，结果吻合较好，对比结果见表2.

图6 差值分析参数曲线

a 350 km·h-1，距离25 m

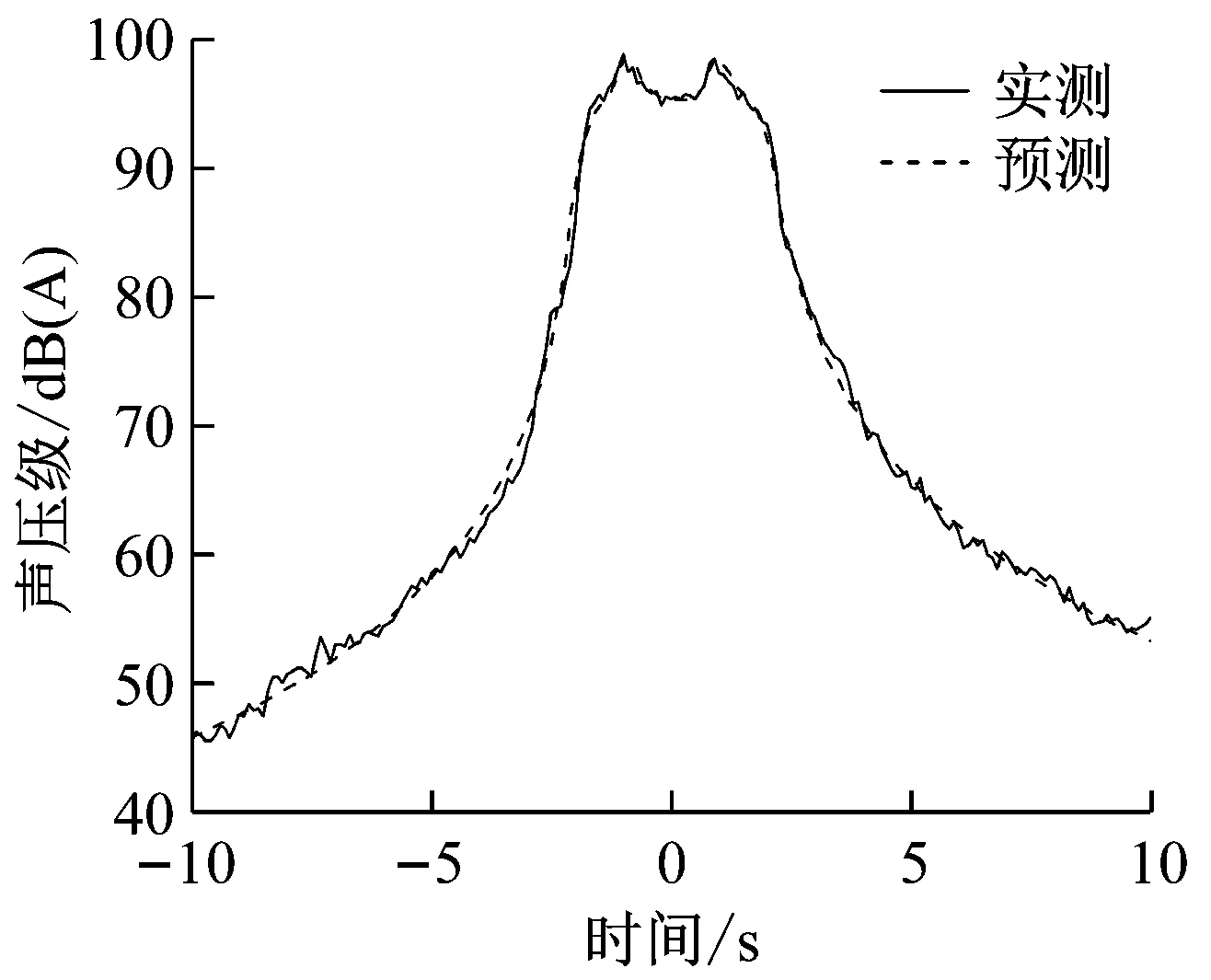
b 380 km·h-1，距离25 m

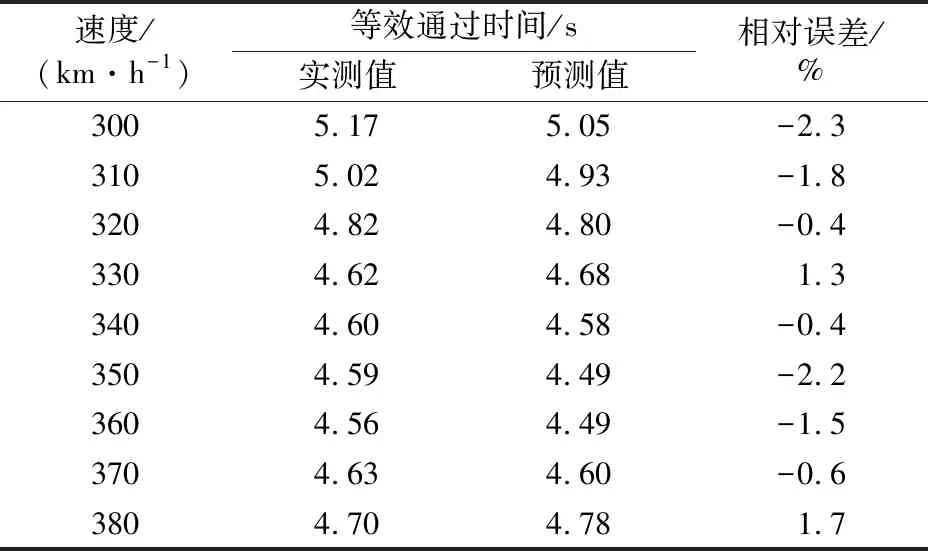
表2 25 m处观察点等效通过时间结果对比

高速列车以恒定速度300 km·h-1运行时，采集不同位置声压级并计算等效通过时间，将实测与预测结果列于表3，同样有较好的一致性.

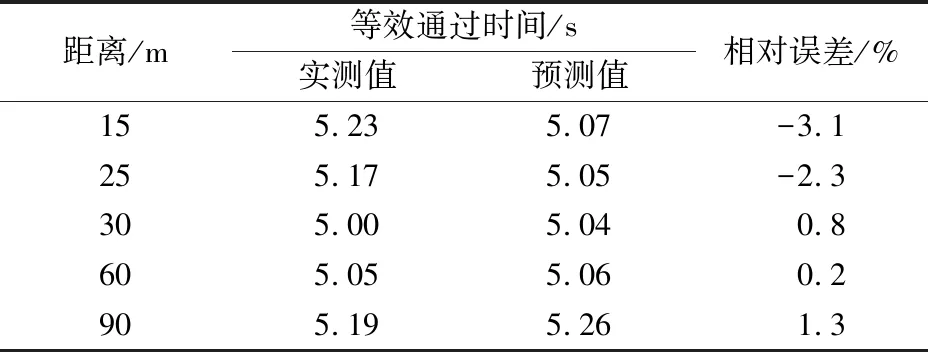
表3 300 km·h-1高速列车等效通过时间随距离变化

3.3 分析

通过改变观察点位置，预测模型可以很快计算出对应的等效通过时间，初步的数据分析显示，等效通过时间随速度和距离有较大变化.为了使研究更具一般性，引入等效通过时间系数Teq,c和距离比D两个参数.

Teq,c=Teqv/l

(22)

D=yK/l

(23)

式中：l为列车长度；yK为观察点K到轨道中心线的距离.

结合等效通过时间预测结果和式(22)、(23)，绘制不同速度下高速列车等效通过时间系数与距离比的关系曲线，如图8所示.

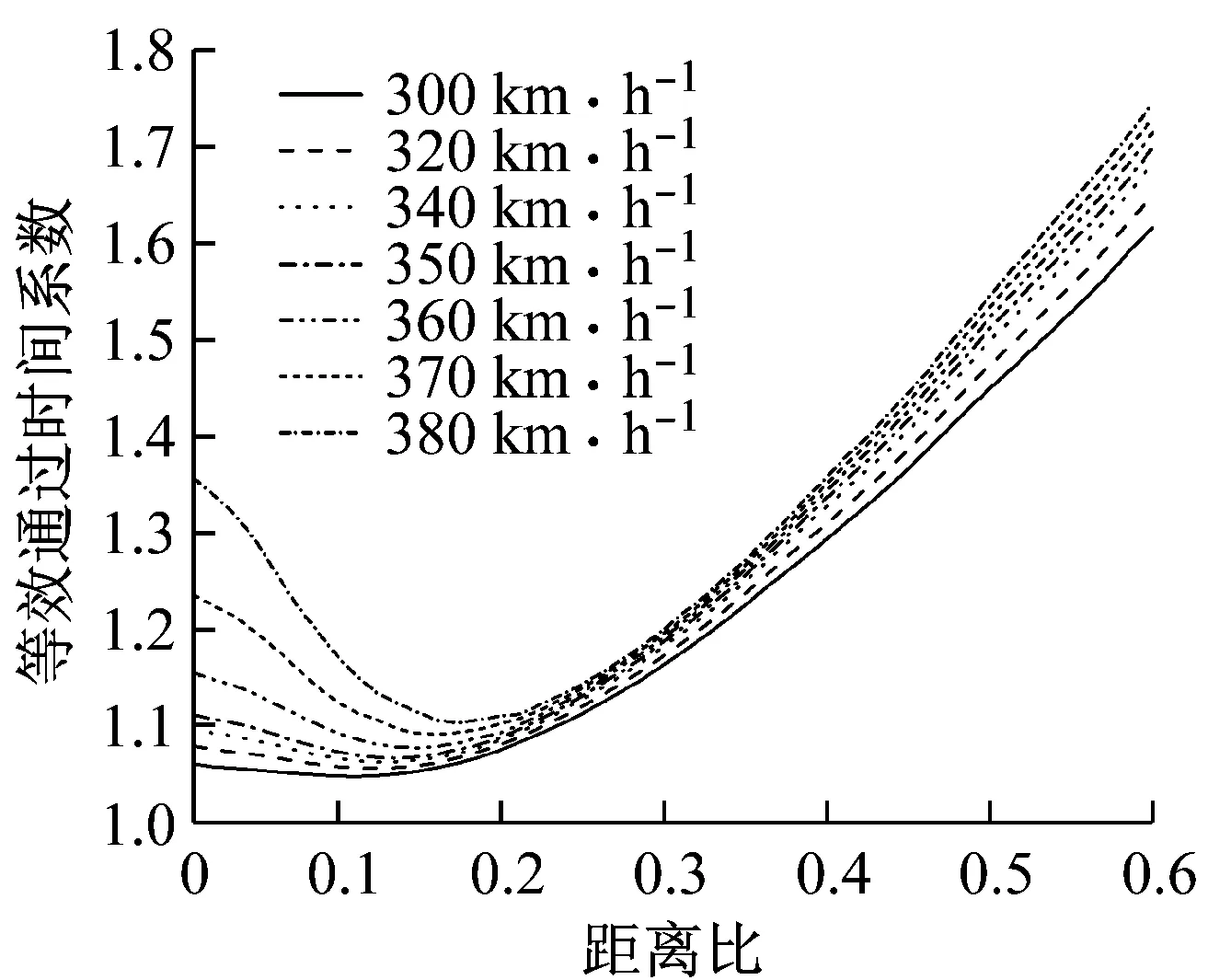
图8 不同速度下等效通过时间系数与距离比关系曲线

高速列车以300～380 km·h-1运行时，等效通过时间系数随车速增加逐渐增大，不同速度下的等效通过时间系数在距离比D=0.250时趋于一致.当D>0.300时，等效通过时间系数与距离呈线性变化，随着速度的增加斜率逐渐变大.当D<0.1时，等效通过时间系数由近及远逐渐减小，并随着车速急剧增加，变化趋势与远场情况相反，以往认为受声点等效通过时间随距离变化规律一致且近点等效通过时间直接等于l/v(即等效时间系数等于1)的结论在高速下显然不成立.图9是距离比为0.075、0.150、0.250、0.500时380 km·h-1高速列车通过噪声预测曲线.

图9 380 km·h-1高速列车通过噪声曲线(距离比为0.075、0.150、0.250、0.500)

Fig.9 Time history of SPL during passage of high-speed train at 380 km·h-1(D=0.075, 0.150, 0.250, and 0.500)

高速列车以恒定速度通过观察点时，随着距离比的不同通过噪声曲线有很大区别.当距离比D=0.075时，对应实际距离为30 m，高速列车通过噪声曲线在受电弓通过时有明显的峰值(受电弓噪声引起的峰值明显高于由中部气动噪声引起的峰值)，列车中部通过时观察点声压级与峰值差值较大，由等效通过时间定义及式(3)，等效时间系数随着车速的提高会显著增加.当D=0.200和D=0.500时，同一速度下的通过噪声曲线趋于平缓，列车中部通过时刻的噪声基本对应受声点的最大噪声级，但随着距离的增加，等效通过噪声峰值偏离t=0时刻更远，列车通过时声能量分布更为均匀，也进一步使得等效通过时间系数随距离增大.

4 结论

高速列车等效通过时间计算的准确性对铁路噪声预测起到非常大的作用，基于高速列车声源分析和声传递关系研究，本文通过理论计算和试验验证优化通过噪声预测模型，基于等效通过时间计算原理推导不同速度和距离比下等效通过时间系数的变化情况，分析这种变化产生的原因.在研究中得出以下结论：

(1) 300 km·h-1及以上高速列车主要声源为以偶极子为主的气动噪声，引入指向性参数n，通过与实测数据的对比和优化，指向性参数n取值0.85.

(2) 基于声传播理论及试验结果建立了高速列车通过噪声及等效通过时间预测模型，与实测数据相比，两者都有很好的一致性.

(3) 通过分析380 km·h-1高速列车不同距离比处的通过噪声曲线，探明等效通过时间系数随车速不断增大，但在近点和远点位置呈相反的变化规律的原因，等效时间系数预测表格可用于实际环评预测.