利用“庞纳特方格法”构建遗传解题数学模型
2019-11-30马晋闽王玉龙
马晋闽 王玉龙


摘要 利用庞纳特方格法构建遗传解题数学模型利于培养科学生的科学思维,便于清晰地认识基因频率、基因型频率的变化规律,为复杂的遗传规律问题的解决提供巧妙便捷的思路。
关键词 庞纳特方格法 基因频率 基因型频率 数学模型
中图分类号 G633.91 文献标志码 B
庞纳特方格法是庞纳特首创的一种棋盘格,常用于分析各种亲本组合类型下的杂交后代的基因型和表现型比率,在国内的生物教学中,经常把这种方法称为“棋盘法”。人教版生物学教科书《必修卜分子与细胞》中指出:“模型是人们为了某种特定目的而对认识对象所做的一种简化的描述,这种描述可以是定性的,也可以是定量的;有的借助于具體的实物或其他形象化的手段,有的则通过抽象的形式来表达”。庞纳特方格法的实质是一种数学模型。
1 庞纳特方格法的基本原理
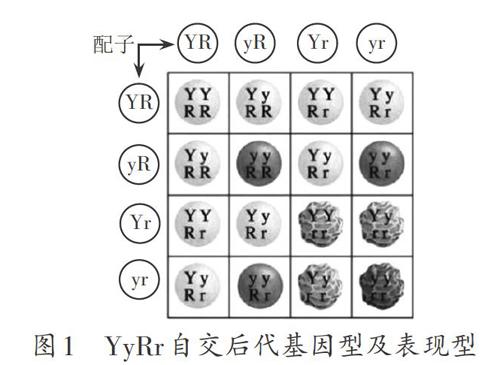
庞纳特方格法的基本绘制原理是,方格的横向(横坐标)或纵向(纵坐标)用于表示遗传过程中亲本所产生的配子的基因型及其比例,方格内的内容即为配子随机结合后所对应的基因型组合,如图1所示。图1为人教版《必修2.遗传与进化》中YyRr个体自交的后代中不同性状自由组合现象的分析图解,横纵坐标表示雌雄个体产生的配子类型,方格内表示各种配子组合得到的个体基因型情况。
庞纳特方格法可根据实际对象的不同,作出一些变形及改进,如在分析YyRr自交所产生子代的基因型时,可将庞纳特方格横坐标变形为表示某一种性状的基因型类型及比例,纵坐标表示另一种性状的基因型及比例,方格内表示各种性状组合的基因型组合及比例,即将图1进行简化,如图2所示。
为通讯作者
当对个体子代进行表现型分析时,可将庞纳特方格变形为横坐标表示个体的某一性状表现型及比例,纵坐标表示另一种性状的表现型及比例,方格内表示各种表现型及比例,如图3所示。
2 庞纳特方格法的应用
模型建构是通过研究模型来揭示原型的形态、特征和本质,是以简化和直观的形式来显示复杂事物或过程的手段。庞纳特方格法作为一种数学模型,为复杂的遗传规律题目的解决,提供了巧妙便捷的解题思路。
2.1 在常规题型中的应用
【例1】低磷酸酷酶症是一种遗传病,一对夫妇均表现正常,他们的父母也均表现正常,丈夫的父亲不携带致病基因,而母亲是携带者,妻子的妹妹患有低磷酸酯酶症。这对夫妇生育一个正常孩子是纯合子的概率是()
A.1/3 B.1/2 C.6/11 D.11/12
参考答案:C。
典型解法:通过题目信息可以推知,丈夫AA的可能性1/2,Aa的可能性1/2。妻子AA的可能性1/3,Aa的可能性2/3,生下一个正常孩子的概率是1-1/2x2/3×1/4=11/12,是AA的概率是1/3×1/2+1/2×2/3×1/2+1/2×1/3×1/2+1/2×2/3×1/4=1/2,因此生育一个正常孩子是纯合子的概率是6/11。
该题目的解题中由于父母双方都存在2种基因型的可能,而且这两种基因型在组合过程中均可以获得AA个体,所以存在4种组合方式,在计算过程比较容易出错。若用庞纳特方格法则可以快速便捷的解题。通过丈夫AA的概率1/2,Aa的概率1/2,则丈夫产生的配子A:a=3:1。妻子AA的概率1/3,Aa的概率2/3,则妻子产生的配子A:a=2:1,利用庞纳特方格法如图4所示,可以看出生育一个正常孩子是纯合子的概率是2/3×3/4/[1-(1/4×1/3) ]=6/11。
2.2 在淘汰或致死题型中的应用
【例2】(2013·山东卷)用基因型为Aa的小麦分别进行连续自交、随机交配、连续自交并逐代淘汰隐性个体、随机交配并逐代淘汰隐性个体,根据各代Aa基因型频率绘制曲线如图5所示。下列分析错误的是()
A.曲线11的F3中Aa基因型频率为0.4
B.曲线IQ的F中Aa基因型频率为0.4
C.曲线Ⅳ的Fmax中纯合体的比例比上一代增加(1/2)n+1
D.曲线Ⅰ和Ⅳ的各子代间A和a的基因频率始终相等
该题目将自交、随机交配,全部个体都能存活和某一种特定基因型致死淘汰等复杂情况结合在一起,是高中遗传学中的一道比较复杂的习题,成为各类教辅及模拟考试必备训练。其中随机交配并淘汰隐性个体,自交并淘汰隐性个体的变化趋势是难点,常见的解题思路是算出各种情况下F1、F2、F3中杂合子的比例,并依据图像作出判断。这种通过特例来判断曲线类型的方法用于解题十分简便。但这种方法缺乏逻辑的严密性与必然性,可以借鉴庞纳特方格法构建数学模型,进而更准确直观反映基因型频率变化趋势。
2.2.1 随机交配并淘汰隐性个体的计算
当父本、母本具有各种比例不同的基因型时,子代基因型及其比例的计算将变的复杂,庞纳特方格法由于关注点在配子而不是个体,所以可以将亲本中不同个体的基因型及比例转换为亲本所能产生的配子类型及其比例,该转换为复杂题目的解答,提供了巧妙便捷的解题思路,如下所示。
杂合子(Aa)连续随机交配并淘汰隐性纯合子
封面照片说明 黑柴胡Bupleurum smithii Wolff.
黑柴胡是伞形科柴胡属的一种多年生草本植物,常丛生,高25~60cm,根黑褐色,质松,多分枝。叶多,质较厚,基部叶丛生,狭长圆形或长圆状披针形或倒披针形。花期7~8月,果期8~9月。分布于河北、山西、陕西、河南、青海、甘肃和内蒙古等省区。生于海拔1400~3400m的山坡草地、山谷、山顶阴处。黑柴胡的根可用于感冒发热。(摄影:李鹏)(aa),F1中Aa比例为2/3,F1中基因频率(或产生的配子)A:a=2:1,如图5a:F1随机交配,F2中Aa比例为2/4,F2中A:a=3:1,如图5b:F2随机交配,F3中Aa比例为2/5,F3中A:a=4:1,如图5c。通过观察三代庞纳特方格法得出的数据可以发现:A与a基因频率(或产生的配子)比例从亲代的1:1,变为F1中的2:1,F2中的3:1,F3中的4:1。由此可知,An中的A与a基因频率的比例应该是(n+1):1。同理可得,杂合子在子代个体比例:F1为2/3,F2为2/4,F3为2/5,故Fn中杂合子的比例为2/(n+2),如图5d。
对上述结论的验证:
若Fn中:A:a=(n+1):1,则Fn-1中可表示为:
A:a=n:1。
由F(n-1)随机交配产生Fo,不淘汰隐性纯合子时,各基因型的比例应为:
AA:n2/(n+1)2,Aa:2n/(n+1)2,aa:1/(n+1)2。淘汰隐性个体后Aa比例应为:2n/(n+1)2/[1-1/(n+1)2]=2/(n+2),与庞纳特方格法直接观察所得的结果一致。
2.2.2 自交并淘汰隐性个体的计算
纯合子自交依然为纯合子,不影响原有比例,而杂合子自交后代中杂合子比例为原有杂合子比例的一半。而这种比例变化关系也可以借助图形进行直观化表达,如图6所示。
图6a中,亲本杂合子(Aa)自交,F,中共有4份,Aa占2份,无淘汰时F1中Aa比例即为2/22=1/2,淘汰aa后F1中Aa比例为2/[(4-2)/2+2]=2/3:图6b所示,F1自交无淘汰时F2中共有8份,Aa占2份,比例即为2/23=1/4,淘汰aa后F2中Aa比例:2/[(8-2)/2+2]=2/5:图 6c所示,F3自交无淘汰时F3中共有16份,Aa占2份,比例即为2/24=1/8,淘汰aa后F3中Aa比例:2/[(16-2)/2+2]=2/9。据此可知,无淘汰时,Aa逐代自交后代的总份数以20.,递增,且Aa所占份数为2份,AA与as的份数相等。所以Aa逐代自交,后代中Aa的比例为1/2n。淘汰aa后,可通过图解法可以得出Aa的比例为:2/[(2n+1-2)/2+2]=2/(2n+1)。
对上述结论的验证:
Aa逐代自交后代中Aa的比例为1/2n,AA比例为(1-1/2n)/20淘汰aa后,Aa所占的比例为(1/2n)/[1/2n+(1-1/2n)/2]=2/(2n+1),与庞纳特方格法直接观察所得的结果一致。
在利用“庞纳特方格法”构建遗传解题数学模型的分析过程中,基于生物学的事实,通过对F,.F2的分析,推理出Fn的情況,培养了学生归纳与概括能力、演绎与推理能力。通过庞纳特方格法和数学方程式两种数学模型的构建,将形象思维与抽象思维进行整合,培养了学生建模的能力与创造性思维能力。
正如《普通高中生物学课程标准(2017年版)》指出:高中生物课程标准是以提高学生生物学科核心素养为宗旨的。学生应该在学习过程中逐步发展科学思维。教师应该重视在日常教学过程中利用相应契机培养学生科学思维。
参考文献:
[1]陈桂林.庞纳特方格在遗传定律学习中的应用[J].中学生物教学,2017,(1~2):43-45.
[2]熊振宇.对2013年高考理科综合试题(山东卷)第6题的剖析[J].中学生物教学,2013,E9): 57-58.
[3]中华人民共和国教育部.普通高中生物学课程标准(2017年版[S].北京:人民教育出版社,2018:4-5.
