扩散场重建格林函数检测钢轨近表面缺陷∗

张海燕 刘建全 张 辉 徐梦云

(1 上海大学通信与信息工程学院 上海 200444)

(2 上海工程技术大学城市轨道交通学院 上海 201620)

0 引言

钢轨的缺陷检测是影响铁路系统安全运行的重要因素，钢轨的腐蚀、内部裂纹和空穴不仅缩短了铁路的服务周期而且带来了潜在的铁路安全危机。因此，研究应用在钢轨上有效的结构健康监测技术具有很重要的实用价值和学术意义。超声无损检测技术是目前最流行的结构健康监测技术，在铁路安全方面发挥着日益重要的作用。超声相控阵是近年主流的超声检测技术，允许应用实验捕获的全矩阵进行后期不同方法的成像技术，具有检测灵敏度高、成像范围大的优势。然而，超声相控阵列采集系统有一定的局限性，具有非线性压电特性的换能器是信号采集系统的基本单元，由于换能器的介质性、机电转换与机械振动的影响，造成超声相控阵的非线性效应，使得早期的声信号变得模糊；换能器的脉冲响应除了包括从发射到接收的散射信息以外，还包含最初激励的残余信息，例如换能器内部的超声波混响信息；紧密排列的超声相控阵阵元使它们之间的响应更加复杂，出现相邻阵元之间电子和机械串扰的饱和问题；最终形成的近表面噪声导致检测系统出现盲区，在工程材料中该盲区可以延伸几毫米。实验中近表面缺陷信息全部湮没在盲区中，这种情况下实现近表面成像已无能为力。尽管在换能器和测试样本之间加上楔块，能够减小非线性效应的影响，但是要以牺牲大部分超声能量作为代价，同时，楔块的加入会导致最终成像结果出现伪像。若超声相控阵不使用楔块直接检测待测样本，近表面信息丢失，典型的全聚焦成像方法和波数成像方法都不能够对近表面缺陷成像，甚至任何成像方法也不能达到近表面成像的目的。

扩散场[1−3]研究的兴起给无损检测领域带来了很大的帮助，理论和实验研究表明能够从一对传感器接收到的弹性扩散场信息评估局部的格林函数响应。2001年前后，Lobkis 等[1]和Weaver 等[2]研究了一个传感器发射的情况下，利用两个传感器接收的扩散信号进行互相关运算能够恢复两个传感器之间的直接响应，增加声源的个数和均值处理可以提高响应恢复的质量。2007年，Sabra 等[3]研究了利用扩散场的互相关特性进行相干导波的提取，并指出完全扩散场能够更好地评估脉冲响应。Duroux 等[4−5]在几何形状复杂的薄铝板上使用激光脉冲产生扩散场并用激光多普勒振动器扫描采集铝板的检测区域，利用扩散场评估任意传感器对之间的第一个反对称Lamb 波的直达信号，之后根据提取的导波结果进一步评估二次声源的数量和位置对扩散函数性能的影响。基于环境噪声的格林函数重建成了学术研究的一个热点。在板状金属的结构监测方面，结合有效的成像算法对铝板的疲劳裂纹进行被动检测和定位，这种技术可能推广于航空航天结构的检测，因为航天器发动机产生的噪声源以及机翼和空气作用产生的摩擦提供了有效的局部环境噪声[6]。在利用环境噪声实现散射体无源成像发展阶段，基于环境噪声的互相关恢复两点之间的格林函数原理，李国富等[7]研究了道路交通噪声场中石柱和海浪噪声场中塑料桶的空间位置定位。在地震学中，Campillo[8]记录了墨西哥两个站点的地震尾波并重建格林函数的可行性，随后通过两个站点之间尾波互相关的均值计算说明重建格林函数具有相位一致性的可能。Chaves 等[9]利用地震噪声的检测描述了哥斯达黎加尼科亚半岛地震后的地震速度变化。近年，基于噪声源产生的扩散场互相关提取格林函数成为了被动检测成像的重要基础。Chehami等[10−11]通过多个传感器的实验装置证实可以用噪声互相关特性计算定位混响弹性薄板中的缺陷，并讨论合适成像和滤波的方法，提高了检测性能。

本文研究了钢轨近表面缺陷的超声相控阵成像技术，提取延迟后一段时间的扩散场全矩阵，然后互相关运算以此产生重建的全矩阵信息，这种重建全矩阵不包含直接检测响应的早期饱和的非线性效应，而是包含被噪声湮没的近表面早期缺陷信息。因此，与直接检测获得的全矩阵相比较，重建全矩阵对早期的信息捕获具有很大优势，因此适合应用在材料的近表面成像领域。

1 扩散场基本理论

超声信号在被检测材料结构中经过足够长的传播时间，尤其是材料的几何结构复杂，自然会引起监测信号的散射和多反射。超声波传入到有界物体之后，在很长的混响时间内，信号的散射、叠加和反射增强了弹性波能量的随机性，结构体中存在着非静态的随机的噪声，该声场为近似均匀化的扩散场。最理想的扩散场是由热波动形成的，能量分布均匀[1−2]。同样，钢轨中的扩散场也具有随机特性，但是传统的结构健康监测方法没有利用此特点。扩散场信号的波形可以用一对接收传感器记录，互相关运算就能获得两个传感器之间的格林函数。常规的主动测试和被动测试提取格林函数的方法截然不同，前者应用一个发射传感器和一个接收传感器组成的收发模式进行格林函数的评估，而后者仅仅采用接收传感器记录环境噪声或者扩散场信息并利用接收信号之间的互相关进行格林函数的评估。实际过程中在被检测的结构中产生充足的扩散场至关重要，因为这一环节直接影响格林函数评估的精度。二次声源的个数和位置的分布直接反映出扩散场的特性的好坏，相控阵线性阵列阵元的线性分布决定了被测样本结构内的扩散场不均匀，最终导致实验提取的扩散场信号不够完美，但是这不会削弱扩散场提取格林函数的理论依据。理论表明[2,7]经过足够长时间的多反射后更有可能提取扩散信号，而且随着二次声源的个数或者扩散场的持续时间的增加，互相关运算得到重建信号的信噪比逐渐增加。图1展示了超声相控阵测试钢轨截面模型的示意图，多反射和多散射后使用相控阵探头获取钢轨中扩散信号，具体实验操作是截取延时一段时间后的全矩阵数据，利用扩散场被动提取格林函数的原理，对两个接收阵元采集的信号进行互相关运算，最终得到的结果是这两个传感器之间的反因果和因果格林函数响应，该响应具有时间轴上的对称性。

图1 钢轨中的扩散场Fig.1 Diffusion field in rails

2 扩散场重建格林函数

2.1 互相关重建格林函数分析

格林函数的提取理论依据目前得到充分的发展，假设扩散场在空间上均匀分布，处于其中的两个接收点分别为r1和r2，则可以得到频域格林函数[12]，

其中，等式的左边表示接收传感器r1和r2之间的因果格林函数和非因果格林函数，右边的积分表达式与互相关函数有关系，r表示扩散场积分密闭空间V中的任一点位置。在声场中假设噪声满足均匀分布且不相关，噪声的功率谱|q(ω)|与位置无关，

结合公式(1)和公式(3)得到

其中，p(r,ω)表示随机噪声下在位置r处的声场，等式左端格林函数G(r1,r2,ω)与它的时间反转项，即频域中取共轭，这两项乘以随机噪声的功率谱密度等于等式右端扩散场中接收传感器r1和r2互相关。将公式(4)转化为时域表达式，2iω对应时域的2d/dt，根据卷积定理可知，频域相乘对应时域卷积，

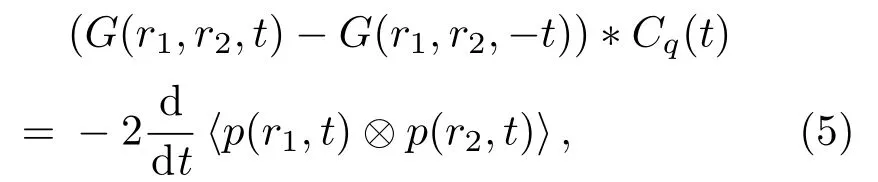
式(5)中，∗表示卷积运算，⊗表示互相关运算，Cq(t)表示扩散场中噪声q(t)的自相关。公式(4)和公式(5)表明扩散场中接收传感器p(r1,t)和p(r2,t)的互相关的导数等价于这两点之间的格林函数，根据声波的互易性，理论上两点之间的格林函数响应在时间轴上具有对称性。

2.2 重建格林函数全矩阵

应用超声相控阵阵元收发功能测试钢轨并直接获得全矩阵数据hi,j(t)，i和j表示一对收发传感器，利用该全矩阵不能够对近表面的缺陷进行成像，此时早期时间的缺陷信息完全被湮没在幅值较大的噪声中，该噪声是由相控阵探头非线性饱和效应产生的，如何提取湮没的近表面缺陷信息是非常关键的环节。图2为实验中相控阵示意图，N个阵元同时具有发射接收功能，采集时间足够长的全矩阵信号hi,j(t)截取时间Tc,以后的时间窗口长度为T的信号作为扩散场全矩阵di,j(t)，此时的信号具有噪声的随机波动性，扩散场充满了整个钢轨结构中。阵元k发射，阵元i和j接收，则接收阵元之间的互相关表示为[6,12−13]

图2 相控阵利用扩散场恢复格林函数Fig.2 Ultrasonic phased array using the diffusion field to recover the Green’s function

为了有效地利用互相关方法重现两点之间格林函数，两个接收传感器对应相同的声源，实际做法是以k为声源遍历所有阵元，计算总体均值，这是评估格林函数的有效途径，N个阵元阵列时域中两点之间互相关表达式为

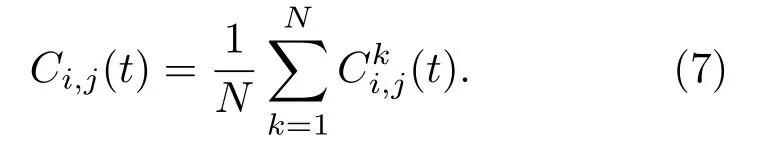
根据上述推导公式，对互相关函数求导，即可得出重建格林函数全矩阵gi,j(t)，

重建格林函数响应的全矩阵gi,j(t)近似于阵元间直接的响应矩阵hi,j(t),实验中Ci,j(t)总是包含多余的波动成分，导致Ci,j(t)在时间轴上不是完全对称的，高水平成分的波动分量直接影响格林函数的精确评估，这些重建误差叫做互相关冗余量[14]。提高重建全矩阵gi,j(t)的质量也就是改善成像结果的目的。该实验与超声相控阵阵元的数目直接有关，同时与截取信号窗口大小T有关，窗口值越大，重建的全矩阵质量就越好，但是以牺牲计算的时间为代价。另一个影响因素就是延时Tc,延时较短，不能够满足扩散场特性；延时较长，扩散场信息复杂，不能恢复早期信息。选取的时间大小根据具体的实验而定，Weaver 等[2]给出了这些参数如何影响格林函数恢复的严谨分析。实验中利用互相关为后续成像提供了基础，借用阵元传递功能近似得到阵元之间的格林函数卷积，这被认为是一种时间反转处理，时间上的后期扩散全矩阵被转换、等效为没有接收延迟的阵元间的直接响应矩阵。

3 钢轨近表面成像

实验研究的对象是钢轨的截面模型，如图3所示，长260 mm，高172 mm，钢轨的近表面有一个直径为5 mm 的人造通孔圆形缺陷，缺陷的上边缘距离钢轨的顶端5 mm，即缺陷分布在距钢轨顶端5～10 mm 处。实验使用法国M2M 公司生产的相控阵仪器，相控阵的两个探头具体参数配置如表1所示，纵波波速为5900 m/s。

图3 钢轨截面Fig.3 Cross section of the rail

表1 超声相控阵参数配置Table1 Parameters configuration of ultrasonic phased array

首先研究了探头A 下全矩阵捕获得到信号，如图4所示，每个信号都做了归一化处理，当i=j时，提取的信号是典型的自发自收的B 扫信号。用16 个阵元的相控阵探头A 采集钢轨的时间长度为0～100 µs 的全矩阵数据hi,j(t)，其中i=j= 8 两个的传感器对应的响应信号如图4(a)所示，可以看出早期的信号几乎被相控阵自身的非线性效应湮没了。经过Tc为600 µs 的延时，截取时间窗口T为100 µs 的扩散场全矩阵di,j(t)，i=j= 8 两个的传感器对应的扩散场信号如图4(b)所示，早期缺陷的信息分布在扩散场中，利用扩散场互相关重建格林函数全矩阵gi,j(t)。图4(c)为i=j=8 两个的接收传感器之间因果格林函数和反因果格林函数，响应信号关于时间轴对称，与理论分析一致，实际过程中关注的有效信息是因果响应，该信号使被噪声湮没的早期近表面缺陷信息得以重现，奠定了近表面成像的基础。因为相控阵阵元的数目有限，经过整体均值处理后得到的重建格林函数全矩阵gi,j(t)只能近似直接测量得到的全矩阵hi,j(t)。虽然使用重建全矩阵能够更好地获取近表面信息，但是钢轨其他区域的信息仍然使用传统直接测量方法获得。用早期时间缺陷信息突显的重建矩阵格林函数gi,j(t)和后期时间信息精确的直接测量全矩阵hi,j(t)相结合，分别在两个部分加上合适的权重就得到对成像最有利的全矩阵fi,j(t)[13]，

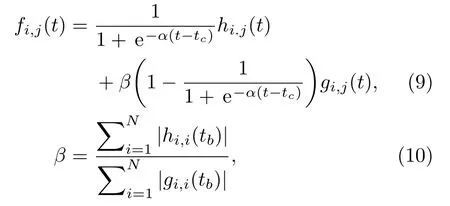
其中，参数β根据第一个散射的回波信息评估，反射幅值的均值被认为每个阵元的脉冲响应在tb时刻的幅值，tc表示过渡时间，值的选择应该在重建矩阵消除非线性饱和效应之后，α表示过渡时的平滑度，取值太小使得非线性饱和效应成分进入fi,j(t)中，取值偏大使得信号过渡突然，不连续，造成成像结果出现伪像。图4(d)是最终合成的重建全矩阵i=j=8 时的信号，与图4(a)相比钢轨近表面干扰噪声得到了有效的抑制，同时近表面缺陷的信息很容易被观察到，重建的全矩阵优势突显，包含了近表面信息的同时也保留了其他区域的有效信息。

图4 i=j =8 时域信号Fig.4 For i=j =8 time domain signals

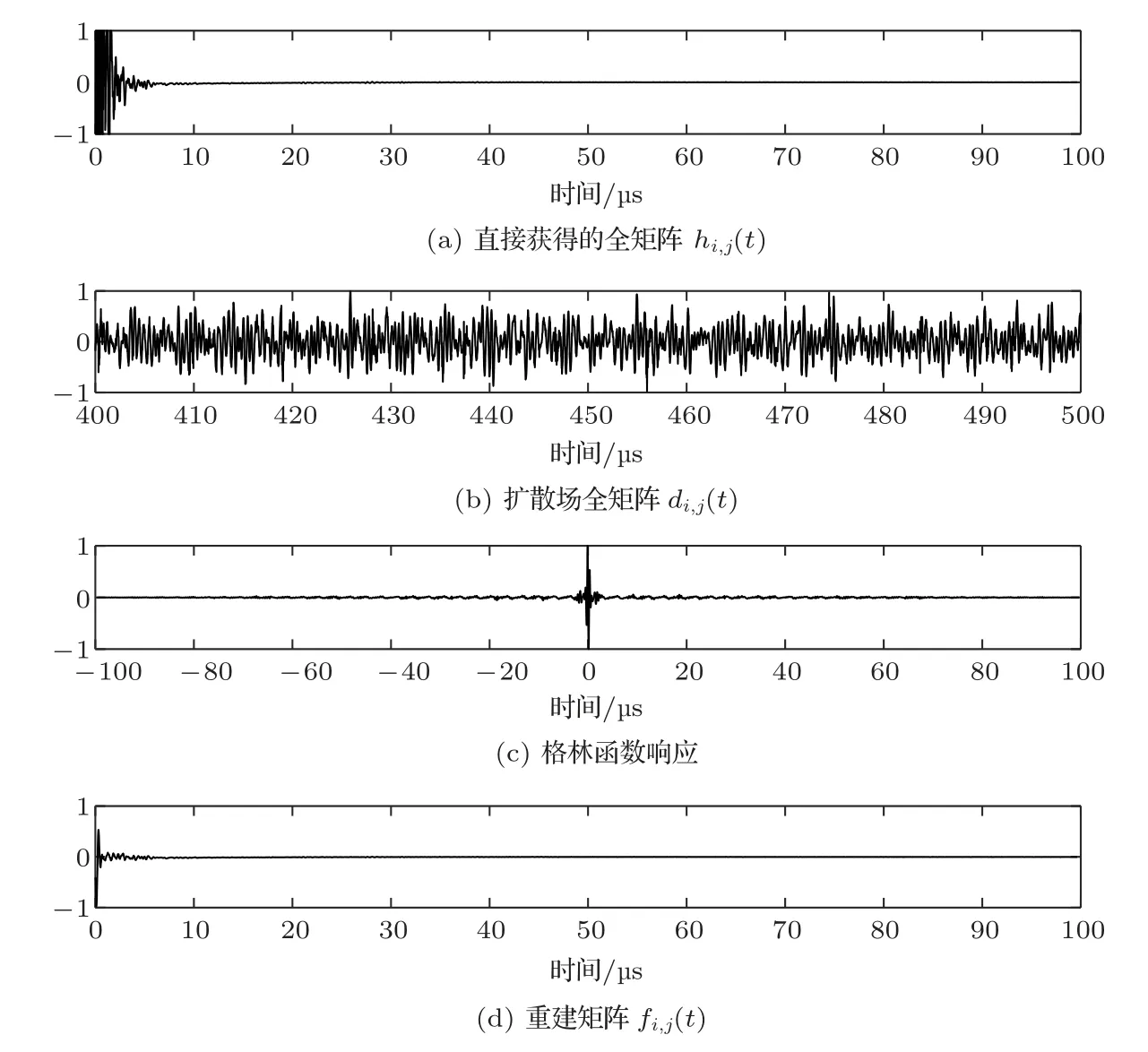
图5 i=j =16 时域信号Fig.5 For i=j =16 time domain signals

然后研究了相控阵探头B 下的信号，超声相控阵探头阵元数为32，激发信号的中心频率为2.5 MHz，如图5所示。图5分别是i=j= 16 时，直接获得的全矩阵hi,j(t)、扩散场全矩阵di,j(t)、格林函数响应和重建矩阵fi,j(t)的信号，此时扩散场信号的经过Tc为400 µs的延时，截取时间窗口T为100 µs。

本文采用快速的波数成像方法[15]对钢轨的近表面成像，使用直接测量得到的hi,j(t)进行波数成像，无论是采用全聚焦方法[16]还是采用波数方法都不能显示钢轨的近表面缺陷。在探头A 的情况下，图6(a)是直接获得数据hi,j(t)的成像结果，可以很清楚地看到高强度的噪声区域沿z方向延伸至20 mm 左右，距钢轨表面5～10 mm 处的缺陷信息完全被湮没了，不能直接呈现出缺陷；图6(b)是对重建矩阵fi,j(t)采用波数成像的结果，成像速度快，横向分辨率显著提高，可以实现钢轨的近表面成像，可以清楚地看到钢轨的一个缺陷位于5～10 mm处，缺陷的大小和形状与真实的缺陷几乎一样，有效地解决了近表面噪声的干扰。

为了更直观地理解近表面成像，定量分析，经过计算探头A 的信号波长为5.9 mm，而钢轨缺陷的上边缘距离钢轨表面5 mm(小于该情况下的一个波长λ)。探头B 采用16 个阵元和32 个阵元分别对hi,j(t)、fi,j(t)进行波数成像，结果如图7所示。hi,j(t)依旧不能够对近表面缺陷成像，而使用重建矩阵fi,j(t)能够清晰地呈现钢轨的近表面缺陷。对比图6(b)和图7(b)，该方法在阵元数量相同的情况下，探头激励越高，缺陷越集中，更接近32 阵元的缺陷成像效果。对比图7(b)、图7(d)，在频率相同、其他参数一致的情况下，随着相控阵阵元数量增加，近表面噪声几乎被抑制，图像的背景噪声显著降低，缺陷的形状有所改善，清晰地还原了钢轨的圆形缺陷。由于探头B的激励信号频率较高，波长变短，成像结果的缺陷比实际的缺陷小，但是并没有脱离理论根据，依然可以准确地定位缺陷的中心位置，更加充分地抑制了近表面噪声信息，更能够支持近钢轨的表面成像。

图6 探头A 的成像效果Fig.6 Imaging effect from the probe A

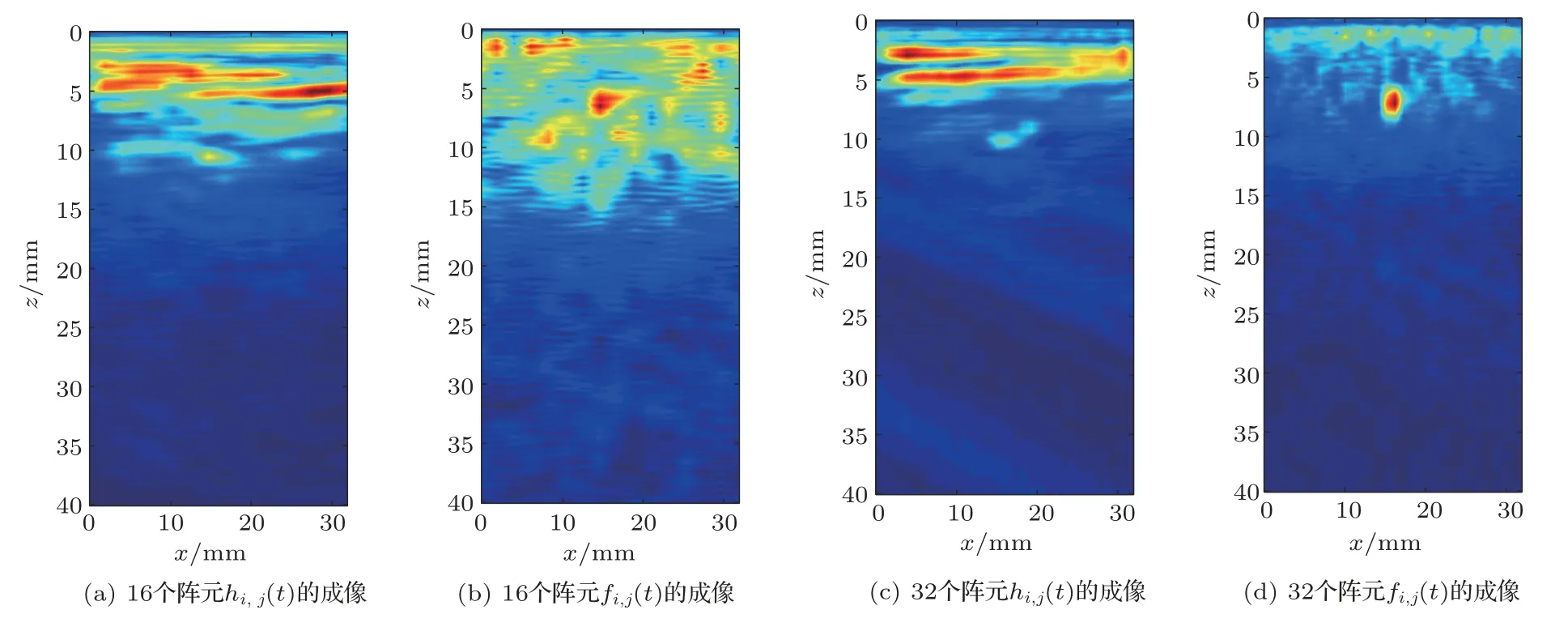
图7 探头B 的成像效果Fig.7 Imaging effect from the probe B

图8 不同参数的三维成像效果Fig.8 3D imaging effect of different parameters

为了更直观地分析钢轨近表面缺陷成像效果，使用归一化的三维图重现图6(b)和图7(b)、图7(d)的结果，如图8所示。对比图8(a)、图8(b)、图8(c)，定性分析信噪比，与相控阵探头A的结果相比较，同时增加阵元个数和激励频率，使用探头B 的波数成像效果有明显的改善，尤其是近表面的噪声几乎被抑制，信噪比显著提升，尤其极大地提高了钢轨近表面缺陷处的信噪比，缺陷处以外的噪声信号迅速减弱，近表面成像取得了非常好的效果。

综上所述，本文使用的互相关方法重建格林函数为近表面成像技术提供有效的捷径，克服了相控阵自身的非线性饱和效应的局限性。

4 结论

本文理论分析了钢轨中扩散场的互相关重建格林函数方法，采用相控阵的全矩阵捕获功能验证了重建格林函数可行性，这是钢轨的近表面成像的核心过程。

(1)实验研究了相控阵两种探头情况下的同一种成像方法，验证了在不同相控阵阵元的激励频率下该方法都能够从扩散场中提取格林函数响应，对钢轨近表面缺陷成像。频率的变化也会影响成像的结果，不同参数相控阵探头获得的实验数据会影响成像的信噪比，当激励频率相同时，尤其相控阵阵元数量越多，重建格林函数的信号就越好，为近表面成像提供了更多的可能性和选择性。

(2)两种超声相控阵探头验证了钢轨近表面成像的可实现性，具有重大的实际工程意义。波数成像方法的优点是横向分辨率率高，呈现出来的缺陷形状与钢轨实际的缺陷完全吻合，清晰地还原了被噪声湮没的缺陷信息，同时该方法也保留了其他区域的有效信息，成功地显示了距钢轨表面5～10 mm处的缺陷，信噪比高，成像效果显著。

(3)论文聚焦钢轨近表面的缺陷成像问题，相控阵探头的配置中心频率为1 MHz 时，其波长λ为5.9 mm，缺陷的上边缘距离钢轨仅5 mm(小于一个波长λ)，提出的方案有效解决近表面成像的问题，把早期时间噪声湮没的缺陷信息完美地恢复出来。