想象力：促进儿童思维发展的重要基石

姚蕊

摘要：儿童善于想象，在数学教学中可以发挥儿童想象之长，通过丰富表象积累素材、类比联想形成技能、试误学习构建场域等途径，进一步发展儿童的想象力。以想象力的发展促进儿童数学形象思维与抽象逻辑思维的发展，为创造力的培养构筑坚实的基石。

关键词：想象力;创造力;思维发展

中图分类号：G623.5 文献标志码：A 文章编号：1673-9094（2019）10A-0077-03

想象是思维的一个特殊范畴，是人对已有的表象进行加工，创造出新形象的思维过程。“想象力则是个体为达到一定的目的、完成某项任务或满足某种期待而借助表象、符号形成某种难以借助五种感官感受到的事物的心智图景或情境能力。通俗地讲，想象力就是个体通过想而改造、重组表象，在头脑中创造一个念头或思想画面的能力。” [1]儿童善于想象，在数学教学中发挥儿童的想象之长，进一步发展他们的想象力，可以为数学的形象思维与抽象逻辑思维搭建沟通的桥梁，促进儿童以形象思维为支点，不断提升抽象思维能力，实现数学思维的全面发展。

一、丰富表象，积累想象的素材

想象是依赖脑内已有的记忆影像及表象而展开的思维活动。表象是想象的基本材料，表象的形成、积累和丰富是想象力发展的基础。发展儿童的想象力，需要链接他们的生活世界、激活儿童的已有经验，在“数”与“形”的探究中实现儿童表象材料的储备。

1.数形相合，构造表象

数是对客观世界中“量”的抽象产物，开展数的认识的教学，需要遵循儿童的思维特点，在经历情境化、直观化的过程中形成数形相合、数境相融的表象材料，为理解数的意义提供直观支撑，为想象力的发展积累素材。

认识自然数时，可以借助小棒、木块、点子图、计数器等直观模型，让抽象的数看得见，摸得着。比如，认识千以内的数，在儿童经历了点子图上圈一圈、用小棒摆一摆、计数器上拨一拨的过程后（如图1），数形相合的表象留存在脑海，“235”这个数就变得具体、真实、鲜活了，不再是一个无意义的、抽象的符号。在认识分数、小数、负数时，则可以通过创设情境、多元表征、模型构造等方式，让抽象的数经验化、具体化。比如，《认识负数》一课的教学，新课伊始之时，让学生自主表达对“-2”的理解。学生们链接生活、联系已知展开想象，有的进行情境创编，有的用实物图表意，也有的用运算来求解，多视角的解读，构成了一组多维度的表象材料，在促进对负数认知的同时，也为想象的展开提供了丰富的材料储备。

当抽象的数与直观的模型、具体的情境建立关联，形成数形相合、数境相融的表象材料，不仅让抽象的数变得可知、可感，同时还为儿童“看数想形”“看数生意”的想象提供了可能。

2.形意相融，丰富表象

图形也是客观现象抽象的产物。认识图形的教学，通常从儿童熟悉的情境入手，选取典型的实物模型，在观察、分析、比较的基础上，逐步抽象概括形成对图形关键特征的认知。之后还需引导他们依据形成的概念展开想象、判别图形、创生表象，不断扩充例证，丰富外延。比如，二年级时要初步认识角、直观认识平行四边形，因为只是初步认识、直观把握，所以教学中不揭示图形的本质特征。学生在形成对角、平行四边形的基本认识后，通过图形识别丰富的正反例证（如图2），使脑内的图形形象不断得到矫正和调试，这对于儿童形成清晰、准确的图形表象显得尤為重要。

想象不是凭空产生的，它依赖于儿童头脑中的表象材料，材料的数量、准确性和清晰度都关系着加工与改造的效果。因此，在数量关系与空间图形的探究活动中，适时地帮助儿童积累丰富多元、清晰可感的表象材料，才能为实现真正的数学想象构筑平台，借助想象的发展实现儿童思维与抽象的数学世界的沟通与关联。

二、类比联想，习得想象的技能

想象力是创造力的起始阶段，想象本身就具有创造性的成分，而实现创造依赖于头脑内已有影像与表象的重组与改造。表象的重组与改造则需要类比和联想的思维方法作为工具支撑。它使在场的与不在场的东西相互关联、相互沟通，构成想象的空间。

1.借助类比寻找思路，生发想象

所谓类比就是寻找两类事物的异同点，加以综合，从而发现它们共同的本质属性的方法。运用类比有助于儿童在比较中将原有的学习经验迁移到新的学习情境中去，根据不同材料生发想象，在对形象材料的加工改造中实现问题的解决。

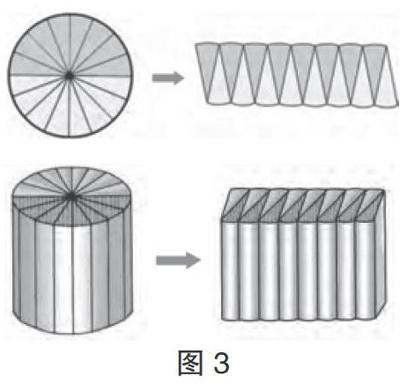
六年级时学生学习《圆柱的体积》，因为圆柱的两个底面是圆形，所以圆柱体与圆是具有关联度的数学表象。教学中，教师有意识地引导学生类比两者，他们便可以从圆的面积推导中获得灵感，由此，适度地想象加工，推及到圆柱体积公式的推导中（如图3）：将圆柱的底面平均分，把圆柱切分为若干等份，拼成近似的长方体，寻求圆柱和拼成的长方体之间的关系，再联系长方体的体积计算公式，便可推导获得圆柱的体积计算公式了。

2.借助联想实现转化，拓展想象

联想是类比的进一步发展，是一种发散式的思维。学会联想有助于儿童面对新问题时进行发散式的思维联结，为创造性地问题解决提供多种路径。

五年级时学生学习《小数乘整数》，教材呈现的是卖西瓜的现实情境，夏天时西瓜0.8元/千克，问买3千克西瓜要多少元？这样显性的情境以及题目中隐含的数量关系都会带给儿童思维的触发。如果由0.8×3联想到乘法的意义，学生便可能用加法运算0.8+0.8+0.8=2.4（元），获得结果;如果由0.8元联想到8角，就有可能转化成整数乘法解决问题，即0.8元=8角，8×3=24（角），24角=2.4元;如果能和计数单位建立关联，便可获得3个0.8合并起来就是24个0.1，也就是2.4的结论。儿童基于在场的数学信息展开联想，建立的联系不同，对表象加工和重组的方式不同，解决问题的路径也就不同。

类比是发现的源泉，联想是创造的基石。在类比与联想中，把不同的形象材料——显性的与隐蔽的，过去的与今天的……交织、汇集在一起，为想象的展开铺就方法的道路，为想象力的发展奠定坚实的基础。

三、試误学习，构筑想象的场域

试误学习，实际上是一种发现学习，它允许儿童在自主探究、自我尝试中发现知识，掌握方法，感悟思想;在迷茫困顿、经历挫折中调整方向，修正不足，获得正解。它允许儿童不断地尝试错误，为儿童提供了自由参与、表达、体验、探究的时空，构筑了想象的场域，重塑了数学课堂的教学样态。

1.在“是什么”的探究中发现

“数学中存在大量的陈述性知识，如数学概念、运算性质、计算公式、数学规律等。”[2]教学中可以把获得陈述性知识的学习转化成对“为什么”的探求，给学生提供试误发现的机会，让儿童在“是什么”与“为什么”的因果追溯中发展想象力、提升学习力，养成善问、好问的习惯。

五年级时学生要学习《圆的面积》一课，没学之前，不少学生已经知晓圆面积的计算方法。此时教学的重心可以放在对“为什么这样算”的探求上。以转化思想为引领，引导儿童将圆与已经学习过的平行四边形、三角形、梯形等直线图形建立关联，鼓励他们在自由想象创造的空间中，动手操作，实践尝试，实现对圆的加工与改造。不同的改造路径会引发不同的公式推导过程，最终，学生们殊途同归，共同验证了圆面积计算方法的合理性。探究“圆面积为什么这样算”的过程是学生借助直观材料经由想象对圆进行改造，借助直线图形面积公式经由推理获得圆面积公式的过程，也是学生的思维由直观形象向抽象逻辑不断进阶的过程。

2.在“怎么办”的尝试中探究

儿童是一个天生的创造者，他们对大千世界万事万物充满着探究的欲望。顺应儿童的天性，数学的学习需要跳出“数学”，走进自然，走入社会，在广阔的世界里发挥数学的用武之地，让儿童在拟定“怎么办”的方案里、在尝试解决问题的过程中，将想象力转化为行动力落实在问题解决中。

四年级时学生要认识三角形和平行四边形，他们走进生活寻找原型，结果发现很多物体中有三角形或平行四边形的元素。在分类对比与实验研究中，学生们感悟到三角形具有稳定性，而平行四边形具有不稳定性，生活中一些物品正是利用了图形的特性而设计完成的。由此，学生们也萌生了做一个小小设计师的愿望。于是，“牙签建高塔”的比赛应运而生：用木质牙签和棱长1厘米的胡萝卜丁为实验材料，设计搭建框架，以能承受50克的重量为标准，比一比哪个小组的高塔建得最高。学生们运用学习所得，充分利用三角形的稳定性，借由想象得以在形象思维与抽象思维的穿梭中，搭建出以三棱柱、四棱柱、五棱柱等为主体的形态各异的复杂结构，把想象力发挥得淋漓尽致。

试误学习，让学生在试一试、探一探的场域中亲历知识形成的过程，习得想象方式与学习方式。而想象方式与学习方式的习得，会运用到其他知识的学习中，让儿童在未来的学习中保持探究与创造的姿态。

想象力具有发散性和创造性，是创造力的起始阶段。没有丰富的想象力，创造力也难以形成。在数学教学中，通过储备清晰可感的表象材料，习得类比、联想的思维技能以及试误学习构建想象的场域等方式，可以有效地发展儿童的想象力，并促进他们形象思维、逻辑思维和创造能力的发展。

参考文献：

[1]张志泉，陈振华.教育应助力儿童想象力的发展[J].中国教育学刊， 2019（2）：54.

[2]曾海英.初中数学教科书中的数学探究活动分析[J].数学教学研究， 2016（8）：11.

责任编辑：颜莹

Imagination： the Important Cornerstone for Promoting

Childrens Thinking Development

YAO Rui

（Xuzhou Minzhulu Primary School， Xuzhou 221000， China）

Abstract： Children are good at imagination and mathematics teachers may help children exercise their imagination in classroom teaching by means of accumulating materials through fertile imagination， analogical association to form skills， and learning by trial and error to construct fields. To lay a solid foundation for childrens creativity cultivation， teachers may utilize the development of imagination to enhance childrens development in their mathematical imagery thinking and abstract thinking.

Key words： imagination; creativity; thinking development