基于插值细分的机械臂手眼标定算法

黄腾超，陈默含，冯勇建，夏荣菲

(厦门大学航空航天学院，福建 厦门 361102)

机器视觉搭配机械臂的开发应用具有自动化、精密化、智能化等特点，近年来被广泛应用于工业生产中.手眼标定作为机器臂匹配视觉系统必不可少的一环，其算法的精确性、稳定性和高效性决定了机械臂在工业生产中的适用性和智能化程度.然而，传统标定算法[1-4]通常是对已知规格标定板上的特征点进行二维图像坐标与三维空间坐标定位，通过计算得到相机焦距、畸变系数、像素实际大小、图像主点等内部参数(内参)，以及相机三维旋转角度和偏移量等相机位姿外部参数(外参).利用相机内参对畸变模型的泰勒级数展开进行拟合，得到消除畸变的真实图像信息;再将真实图像与外参构建的旋转矩阵和平移矩阵进行矩阵耦合运算，确定相机坐标系与世界坐标系的关系.这种算法虽然可以适用于大多数相机标定，但是其标定精度完全依赖初始的相机内参以及旋转矩阵和平移矩阵的求解.相机焦距、畸变系数、旋转矩阵和平移矩阵对于标定板的规格选择以及视觉主点的定位精度要求极高，而这些参数在求解过程中容易出现误差.在大视场的环境条件下，相机内、外参数的求解稍有误差，便对最后的标定精度影响很大.同时，传统标定算法因为对矩阵求解速度的考量，仅考虑二阶以内的径向畸变，使得在畸变较小与较大的区域内，拟合的畸变模型无法完全匹配固有存在的高阶畸变，从而使标定结果出现不稳定的情况，导致无法预测的误差.在实际运用中，像素为千万级的相机在采用传统算法对1.5 m×0.75 m的工作平面进行标定时，误差精度一般在3～6 mm之间[5]，无法满足工业生产的精密性要求.

针对传统标定算法的不足之处，本文中提出一种基于插值细分和运动限制的固定视点下的手眼标定算法.该算法利用机械臂做纵向与横向的自动增量运动，对目标区域的位置信息进行采集，并细化标定区域，通过插值逼近算法拟合畸变曲线，使得标定平面的像素坐标系与机械臂基坐标系实现一一对应的转换关系，从而实现高精度的手眼标定.

1 标定原理

1.1 相机标定原理

机器视觉处理定位问题时的关键在于从相机获取目标图像的信息中计算出三维空间物体的几何信息，以此对图像中的目标进行重构和识别.由于空间中点的三维几何位置与其在图像中的对应点之间的相互关系是由相机的成像模型决定的，所以在标定过程中，标定平面的选取和对成像模型的计算决定了标定精度的水平.机器视觉系统中的手眼标定是为了获取图像坐标系(xc,yc,zc)与机械臂基坐标系(xr,yr,zr)以及世界坐标系(xw,yw,zw)三者之间的转换关系.如图1所示，O为图像主点，Cx、Cy为主点图像坐标，Sx、Sy为像素在世界坐标系的实际大小.在进行手眼标定时，若机械臂的坐标系固定，且具有较高的精度和稳定性，可以将世界坐标系与机械臂基坐标系二者作为一个整体进行考虑，即直接寻求图像坐标系与机械臂基坐标系之间的转换关系[6].

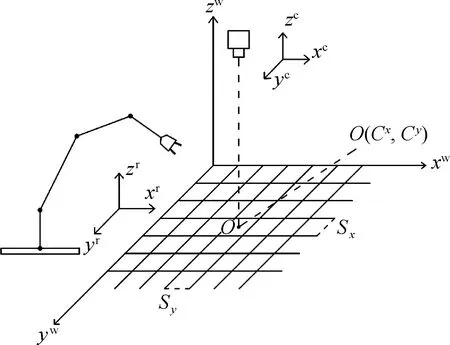
图1 坐标转换关系Fig.1 Coordinate transforming relations

1.2 相机畸变模型

相机镜头上光学透镜固有的透视失真引起的图像畸变常见的有径向畸变和切向畸变.但研究表明[7-9]，在校正模型中引入过多的畸变校正参数，可能会增加计算的复杂性，导致计算结果不收敛而得不到高精度的标定.一般情况下，相机的切向畸变主要是因为镜头透镜与成像平面不平行而产生的，镜头模组上的安装偏差，会导致采集图像平面的偏斜.但是在实际操作中，保持镜头与工作平面近乎水平的条件下，就可以避免明显的切向畸变产生.因此，在镜头与工作平面近乎水平的条件下，引入切向畸变模型，不仅对提高手眼标定精度的作用不大，而且反而会增加计算的复杂性，导致计算结果不收敛[10].因此，本文中只考虑径向畸变模型.

径向畸变[11]是沿着透镜半径方向分布的畸变，产生原因是经过透镜的光线发生不同程度的偏折，而导致图像点在远离主点的地方比靠近主点的地方产生更大的径向位移.如图2所示，根据产生径向位移的正负向关系，径向畸变又分为桶形畸变和枕形畸变.

图2 枕型畸变(a)和桶型畸变(b)Fig.2 Pincushion distortion (a) and barrel distortion (b)

从图2可知，径向畸变成像光轴中心不产生畸变，沿着镜头圆心向边缘移动，畸变越来越严重.畸变的数学模型可以用主点周围的泰勒级数展开式的前几项进行描述，通常取前两项，对于畸变严重的镜头取3项或者更多项.张氏标定法[12-13]提出，畸变图像上某点的像素点坐标可表示为：

xu=xd+(xd-xo)(k1rd+k2rd2+…),

yu=yd+(yd-yo)(k1rd+k2rd2+…).

2 基于插值细分的手眼标定方法

通过上述对畸变模型的分析可知，影响标定精度的因素主要为由光学透镜造成的径向畸变影响，而径向畸变可以通过泰勒函数展开式逼近来描述;但是在实际工作中，只能在误差允许的范围内取有限阶，通过高阶泰勒函数逼近的径向畸变模型只能近似于真实的径向畸变.因此，泰勒多项式阶数的选取对于畸变模型的还原起到至关重要的作用.但是，在实际操作中，依靠高阶泰勒多项式来还原采集图像中的径向畸变，会降低标定算法的运算速度，无法达到实际运用中高效、精确的需求.

因此，在处理径向畸变的标定模型上，本文中提出一种基于密集标定点的插值细分算法.插值细分算法易于产生性能良好的曲线曲面，且具有简洁高效和计算速度快等优点，符合手眼标定中快速、精确的需求.

2.1 插值细分原理

其中，ω=1/16的极限曲线有较好的连续性.对于控制顶点集的控制点进行相同的细分规则，获得新的插值点，循环往复，通过l次细分，便可获得2ln+1个插值点.如图3所示，以曲线①中5点为控制顶点集，通过对控制集进行一次插值可得到9个插值点构成的曲线②，然后再以曲线②中各点作为控制顶点集，进行二次插值则可获得17个插值点构成的曲线③.根据插值细分法的定理可知这些插值点收敛于一条极限曲线上[16].

图3 插值逼近示意图Fig.3 Diagram of interpolation approximation

插值细分在细分过程中每一步都不会改变旧控制点的位置，故在用插值逼近畸变曲线处理径向畸变的过程中，插值曲线经过每一次细分过程生成的控制点并不替代原控制点的位置，保证曲线的真实性.

2.2 插值点生成

生成标定点控制顶点集，首先要对标定平面的标定点进行采集，如图4(a)所示，将易识别的标定特征圆架接于机械臂末端，并控制机械臂做自动增量位移，可以遵循先横后纵的遍历方式.机械臂每次位移2 cm，同时，用相机抓拍每一次位移的特征圆位置，利用图像处理立即定位出标定特征圆的圆心图像坐标，并访问机械臂回传参数，记录下每次位移的机械坐标，采集到的点如图4(b)所示.

图4 标定平面的标定点采集Fig.4 Calibration point acquisition of calibration plane

由畸变模型可知，图像中水平直线和竖直直线上的径向畸变曲线较为齐整，不会出现明显偏折.因此，根据四点插值算法的细分规则，可对采集的标定点进行细分，便可还原现实中在直线上的点对应于图像上的畸变点.具体细分的步骤如下所述：

1) 将采集到的图像坐标细分为若干个5×5的方块，每个方块都可被定义为

2) 然后按行进行提取，则可获得5个点构成的控制集

Pi(0)={m(i,0),m(i,1),m(i,2),m(i,3),m(i,4)}，(i=0,1,…,4).

3) 根据插值细分原则，对5个控制集进行3次插值，取第一行为例：

经过3次插值，每个控制集均可细分为出33个插值点

(i=0,1,…,4).

4) 将扩充的插值点重新归纳，则原矩阵扩充为5× 33的矩阵

5) 同理，对新矩阵M1的列进行插值细分，则有新的33个控制集数

Pj(0)={m(0,j),m(1,j),m(2,j),m(3,j),m(4,j)},

(j=0,1,…,32),

继续进行细分，则可得扩充后的33×33矩阵

因为对应标定点之间距离较小，所以，经过插值算法，可生成一个间距几近相同的密集点阵，其中每个点都包含图像坐标与机械臂基坐标系，为方便调用可保存于矩阵文件中.

由标定原理可知，手眼标定的关键在于如何求出机械臂基坐标系与图像坐标的转换关系，根据微分原理可知，通过多次细分后，每个插值点之间的曲线可近似于直线.由于相机畸变模型的曲线较为平缓，所以可以将3次细分后的密集标定点阵切分为1 029个2×2的区域点阵，如图5，每个点阵内区域可用线性关系求解.

图5 目标点落点定位Fig.5 Location of object points

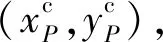
3 实验结果和分析

图6 实验装置图Fig.6 Experimental equipment

本次实验所用的机械臂型号为安川MOTOMAN-MH24机械臂，相机型号为海康威视MV-CE100-30GM面阵相机，易识别的特征圆点直径为4 cm，采集平面约为150 cm×70 cm，图像大小为3 840像素×2 748像素，具体实验装置图如图6所示.此外，利用HALCON编写特征点识别程序，并通过Visual Studio 2017编写控制界面，两者联用完成数据采集和处理.

3.1 手眼标定实验

根据不同区域的畸变程度不同共设计3次实验，每次分20组，共采集200个标定点进行标定误差计算.第一次实验随机选取20个区域，让机械臂在标定区域内自由移动，每个区域取10个目标点，计算平均误差.此外，为验证插值算法拟合畸变的准确性，设计第二次实验随机选取图像边缘畸变较大区域，而第三次实验随机选取图像中心附近畸变较小区域.同第一次实验一样，第二、三次实验每次也取20个区域，每个区域取10次目标点.

同时，以传统标定算法作为对照组进行实验，其标定模板如图7所示.传统标定算法主要通过标定模板计算相机内部焦距、畸变系数等参数还原畸变图像，再利用外部旋转矩阵和平移矩阵矫正相机位姿，从而将相机坐标系与世界坐标系联系起来.此次传统标定算法中的相机内、外参数由HALCON自带标定程序计算得出，参数详见表1.

图7 标定模板图Fig.7 Calibration target

相机内参相机外参名称数值名称数值焦距f/mm 60.353X轴旋转角/(°)359.905畸变系数k-27.169Y轴旋转角/(°)0.012像素大小Sx/μm40.292Z轴旋转角/(°)359.921像素大小Sy/μm40.300X方向平移量/mm4.495图像主点Cx1 948.004Y方向平移量/mm1.916图像主点Cy1 129.121Z方向平移量/mm1.895

利用机器臂末端的特征点在固定标定平面上不规则的增量运动，通过比对机械臂回传的自身位置坐标和图像识别转换后的位置坐标，计算出标定算法的实际误差.设机械臂回传的真实位置坐标为(xr,yr)，根据图像坐标转换的位置坐标为(xt,yt)，用二维欧几里得距离E来表示误差，则

上述的误差是机械臂基坐标系上的误差，机械臂每位移一次，相机采集一次图像，比对机械臂回传的位置坐标和图像识别转换位置坐标计算一次实验误差，设n为采集次数，定义平均误差∂为：

3.2 实验数据和误差分析

通过平均误差计算公式，对实验数据进行标定精度的误差分析，即将实验采集数据代入误差公式.通过对两种标定方法在不同标定区域的平均误差计算，根据所得数据整理得出图8.由图8可知，插值细分法的误差曲线较为平稳，而传统标定算法的误差曲线稳定性较差.插值细分法的误差几乎都在1 mm以内，而传统标定方法误差分布在1.5～5 mm之间，插值细分法标定精度明显更高.

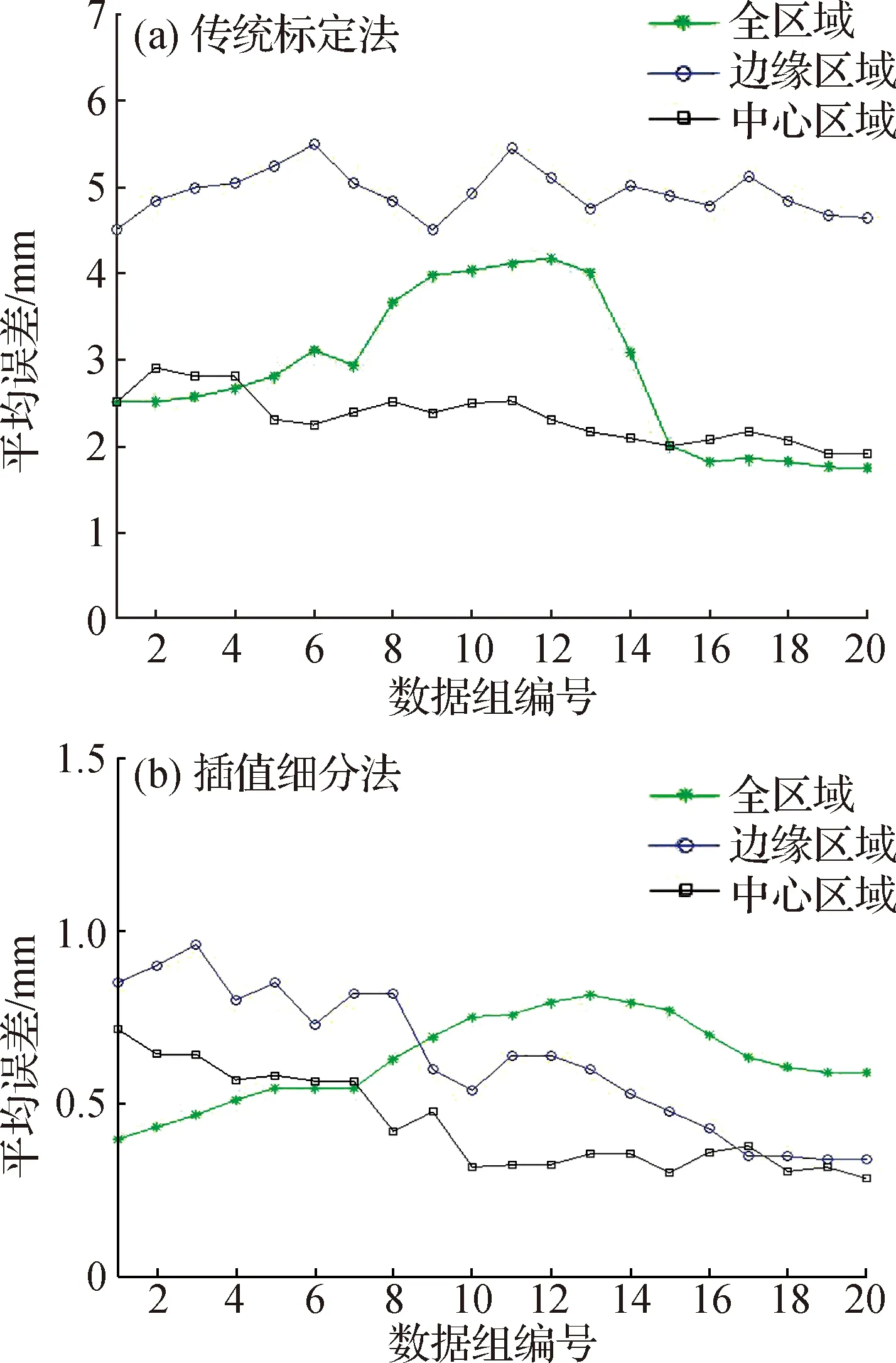
图8 平均标定误差Fig.8 Average calibration error

此外，由图8中传统标定法和插值细分算法在全区域的误差曲线可以看出，6到13组的误差明显高于其他组.经分析，其原因是6到13组的测试点都选取在图像畸变严重的图像边缘.而对比图8(a)和图8(b)中边缘区域与中心区域的标定误差可发现在畸变严重区域，两种标定方法的平均标定误差明显增大.但传统标定算法平均误差高达5 mm，且十分不稳定.而插值细分法，虽在畸变明显的区域误差略有增大，但其最高误差不超高1 mm，平均误差基本稳定在0.3 mm.实验证明基于差值细分的标定方法可以，其标定精度满足实际的工程运用.

图9中(a)～(d)为插值算法运用在工业点胶机械臂上的实际效果图.图9(a)为图像处理的工件边框效果图，通过对工件边框进行识别定位得到工件边框的图像坐标，然后由插值标定算法的坐标转换将图像坐标转换成机械坐标，并将数据传给机械臂.图9(b)～(d)为实际机械臂在工件边框涂胶的效果图，可以看出，胶枪走的路径与图像识别规划的边框路径基本一致.

图9 实际应用效果图Fig.9 Practical application effectiveness

4 结 论

根据实验结果和实际应用效果，针对固定视点的手眼标定系统，本文中提出的基于差值细分算法的标定方法不仅能够简单快速地完成标定工作，还能减少传统算法中存在的标定误差，标定精度在1 mm以内.该方法通过机械臂的自动位移解决传统标定算法中求取相机内、外参数的繁琐步骤，改进了目标点图像坐标系和机械臂基坐标系之间的转换方式，使标定更加便捷、易操作，符合现代工业生产高效率、高精度的需求.