一维Helmholtz方程的优化差分法
2019-11-29周鲁川吴亭亭
周鲁川 吴亭亭
( 山东师范大学数学与统计学院,250358,济南 )
1 引 言
考虑如下一维Helmholtz方程

一维Helmholtz方程在地球物理和医学成像等领域有着广泛应用. 因此, 研究一维Helmholtz方程的高效数值算法具有重要的理论意义和应用价值. 目前, 数值求解Helmholtz方程的主要方法有:有限元法[1]、差分法[2]等. 有限元法的精确性高, 易于边界条件的处理, 但其计算量相对较大, 不利于大规模的计算.差分法计算简单, 存储量小, 易于实现, 并且可以通过优化差分系数的方法来提高差分法的数值精度[3].因此, 本文将重点讨论一维Helmholtz方程的优化差分法. 具体地, 我们提出了一维Helmholtz方程的带参数的差分格式, 证明了该格式为二阶格式. 基于极小化数值频散的思想, 提出了差分格式的优化系数的整体选取法和加细选取法. 最后通过数值试验比较了不同差分格式的精度和数值频散情况, 数值结果表明了本文所提格式提高了数值精度, 有效地抑制了数值频散.
2 Helmholtz方程的优化差分法
本节将对方程(1)建立带参数的差分格式, 并对其进行收敛性分析和频散分析, 最终给出差分格式的优化系数的整体选取法和加细选取法.
2.1带参数的差分格式的建立本小节建立一维Helmholtz方程的带参数的差分格式.

(4)
故令uxx(x)的近似为
(5)
其次, 由(4)式知
u(xi+1)+u(xi-1)≈2u(xi),
则可令k2u(x)的近似为
(6)
其中,c+d=1.
最后, 联立(4)和(5)得到方程(1)的差分格式为
(7)
这里fi=f(xi).
2.2收敛性分析本小节将对差分方程(7)的解进行误差分析, 有如下定理1成立.
定理1 假定u是方程(1)-(3)的解,f是足够光滑的, 且kh足够小, 则差分格式(7)得到的差分解U是唯一的, 且有如下估计
||U-u||≤Ch2.
证为简化证明过程, 假设u的边值条件是Dirichlet边值条件, 带有Neumann边值条件的情况可类似证明. 首先, 将差分格式(7)表示为矩阵形式:
DU=b,
(8)
其中,
(9)
b=(f1,f2,…,fN)T.
因kh是足够小的, 所以矩阵(9)为严格对角占优矩阵. 因此, 方程组(8)得到的差分解U是存在唯一的.
下面, 建立差分解和真解之间的误差方程. 为此, 令ei=u(xi)-Ui,则有
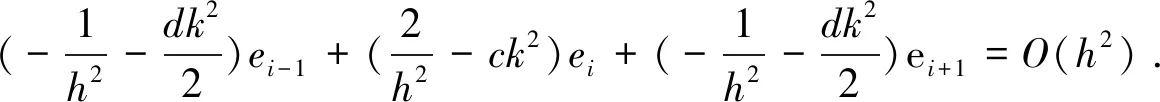
将上述误差方程表示为矩阵形式
DE=T,
(10)
其中,E=(e1,e2,…,eN)T,T=(T1,T2,…,TN)T,Ti=O(h2).
接下来, 进行误差分析. 当kh→0, 矩阵D趋于如下矩阵
(11)
又矩阵(11)的特征值[4,5]为
相应的特征向量为
当h是足够小时, 易知
(12)
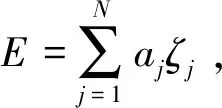
(13)
其中,aj是元素ζj的系数.
并由(10)得到:
(DE,E)=(T,E).
(14)
当kh→0, 应用(12)和(13)以及Cauchy不等式, 有如下结论:
且又因
(T,E)≤||T||||E||,
根据(14)并联立上述两个不等式得到结论.
从上述定理中, 可以看出差分格式(7)在c+d=1的条件下, 是一个二阶格式.
2.3数值波数与真实波数之间的误差分析对于大波数问题,Helmholtz方程的解具有较强的振荡性. 事实上, 随着波数k的增加, 数值解的精度在降低—即所谓的“污染效应”. “污染”的结果就导致数值解的波数不同于真实的波数, 这就是所谓的“数值频散”[1,6]. 在本小节中, 我们将分析差分格式(7)的数值波数与真实波数之间的误差.

接下来, 将Ui:=e-ikxi代入(7)式, 取fi=0, 并利用欧拉公式, 得频散方程:
2AScos(kh)+A0=0,
(15)

(16)
在如下定理2中, 我们将给出数值波数kN和真实波数k之间的误差分析.
定理2 对于差分格式(7), 有
(17)
证令τ:=kh. 又因方程(16)中P依赖于τ, 故P(τ)=cos(τ). 引入记号:
f1(τ)=2-2cos(τ),f2(τ)=dcos(τ)+c.
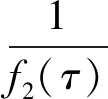
(18)
(19)
结合方程(16)、(18)、(19), 可得到
上述定理表明了kN以二阶近似k. 此外, 与k3h2有关的项称为污染项, 它依赖于波数k和差分格式(7)中的参数.
2.4优化参数选取策略在本小节中, 基于极小化数值频散的思想, 我们给出差分格式(7)的优化参数的两种选取策略. 具体地, 极小化数值频散就是要极小化数值波数与真实波数之间的误差. 研究表明, 差分格式的数值频散越小, 其数值精度越高[7,8].
(20)
其次, 为选取合适的参数c,d来极小化数值频散, 令
其中d∈R,G∈IG. 通常, 选取IG:=[Gmin,Gmax]=[4,400][7], 其中Gmin为G的最小值,Gmax为G的最大值, 并且Gmin≥2[7].
通过(20)可以看出, 极小化数值波数kN和真实波数k之间的误差等同于极小化范数||J(d,G)||, 在此总结为如下选择策略来选取参数d.
1) 整体的参数选取方法.
在给定的条件IG:=[4,400]下, 选取d∈(0,1]以满足
d=argmin{||J(d,G)||,d∈R}.
(21)
下面,利用最小二乘法极小化目标函数(21)的方法[7]来实施选择策略1.若令
J(d,G)=0,
通过整理得方程:
2π2(1-P)d=2π2+G2(P-1).
(22)

故可得到线性方程组
S1d=S2,
(23)
其中
方程(23)的系数矩阵有r行和1列, 是一个超定方程组. 选择r=100, 并用最小二乘法去解方程组(23), 得到差分格式(7)的一组优化参数为:
c=0.817 7,d=0.182 3.
(24)
为方便引用, 我们称带有参数(24)的差分格式(7)为一维Helmholtz方程的整体三点差分格式(简称为global 3p).
整体的参数选取方法只给出一组优化参数, 这种做法比较粗糙. 为进一步提高差分格式的数值精度, 我们提出加细的参数选取方法.
2) 加细的参数选取方法.
估计区间IG:=[Gmin,Gmax], 选取d∈(0,1]以满足
d=argmin{||J(d,G)||,d∈R}.
加细的选择方法与整体的相比, 一个重要的区别是区间IG是根据实际情况变化的. 在表1中, 列出了多组加细的优化参数. 我们称带加细优化参数(表1)的差分格式(7)为Helmholtz方程的加细三点差分格式(简称为refined 3p). 另外, 称带有参数c=1,d=0的差分格式(7)为传统的三点差分格式(conventional 3p).

表1 加细优化参数

3 数值算例
考虑问题(1)-(3), 取f(x)=-1. 此时真解为

图1 三种差分格式数值相速度曲线
接下来, 我们需要对边界条件(3)进行二阶近似.为此, 由Taylor公式得
又因u(1)(xN)=iku(xN)及u(2)(xN)=-k2u(xN)+1, 故边界条件(3)的近似为
(25)
基于上述问题,我们将比较三种差分格式的数值精度: 一种是传统的三点差分格式(conventional 3p), 一种是整体三点差分格式(global 3p), 一种是加细三点差分格式(refined 3p). 在计算中, 误差范数采用相对C-范数. 其中, C-范数具体定义为: 对任意复向量z=[z1,z2,…,zM],

表2与表3对应于k=30,200时, 不同的网格点数(N)下所对应的三种差分格式的相对C-范数误差. 由表2与表3看出, refined 3p的数值精度比conventional 3p和global 3p高. 从表3中还可看出refined 3p在N=513时便可达到global 3p在N=1 025时的数值精度. 这就意味着, 当采用refined 3p时, 可用较少的网格点数得到具有较高精度的数值解. 进一步, 图2和图3表明上述三种格式均为二阶格式. 因此, 在计算中refined 3p相比其他两种格式有着显著的优势[9,10].

表2 k=30时相对C-范数下的误差

表3 k=200时相对C-范数下的误差

图2 k=30时相对C-范数下的误差

图3 k=200时相对C-范数下的误差
为进一步比较三种差分格式的计算效力, 图4(a)与(b)分别给出了三种差分格式在条件kh=1,kh=0.5下的相对C-范数误差. 从图4可以看出, 当kh是一个常数时, 即每个波长内取的网格节点固定时,refined 3p的误差较之其他两种差分格式的误差要小. 而且, 随着波数k的增大, refined 3p的误差增大的更缓慢一些. 这些都表明, 我们所提的格式refined 3p有效地提高了数值精度, 抑制了数值频散[11,12].
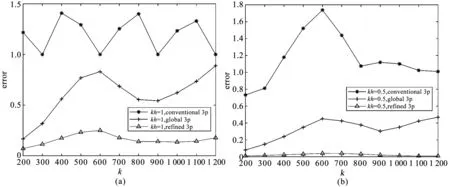
图4 k∈[200,1200]时, 相对C-范数误差
4 结 论
在本文中, 首先基于加权平均的思想建立了带参数的差分格式, 分析了格式的收敛性. 接下来, 给出了数值波数和真实波数之间的误差, 并基于极小化数值频散的思想提出了两种参数选取策略. 最后, 数值算例表明带加细化参数的差分格式提高了数值精度, 有效地抑制了数值频散.
