地震荷载下高含冰量冻土的动力特性试验研究
2019-11-29许俊豪陈页开霍晓辉甄晓霞郑剑锋
许俊豪,陈页开,霍晓辉,甄晓霞,郑剑锋
(1.华南理工大学土木与交通学院,广州 510640; 2.中国科学院寒区旱区环境与工程研究所冻土工程国家重点实验室,兰州 730000)
引言
由于我国“一带一路”倡议的持续推进,交通基础建设逐渐向西北寒区扩展,而在建设中通常会遇到高含冰量冻土,已建成的青藏铁路勘察表明,有221 km 通过高含冰量冻土区[1]。而且西北寒区是一个地震频繁发生的地区,多年冻土区大多位于7度地震区,部分位于8度地震区。高含冰量冻土在地震荷载作用下,其变形和强度不同于一般冻土,因此,为了对寒区地区的工程进行抗震分析,需对高含冰量冻土在地震荷载下的动力特性进行分析,研究高含冰量冻土的动应力应变关系和动力学参数的值及其影响因数,从而确定寒区地区工程的地震反应。动弹性模量是动力学参数的重要组成部分之一。
目前国内外学者对冻土的动力学特性的研究大都是集中在低含冰量冻土和振动循环荷载这两种情况。Chaichanavong对冻土进行了低温三轴试验,研究了杨氏模量、阻尼比与温度等变量的关系[2]。Li等研究了冻结砂土在温度-1~-10 ℃、围压0~1.378 MPa情况下动弹性模量和阻尼比随频率等变量之间的变化规律[3]。何平对冻土施加恒应力幅值动单轴荷载,得出频率对冻土的影响取决于冻土的固有频率[4-5]。吴志坚等对低含水量冻土进行了地震荷载动三轴试验,得出温度对动弹性模量的影响[6]。赵淑萍等采取了粉质黏土和细砂两种土样,对其进行恒应力幅值动三轴试验,分析了动弹性模量随频率增加而增加[7]。常小晓等分析了试验条件对冻土的影响,给出恒温和围压固结的最优化时间,给试验提供一个规范[8]。何菲等得出冻结砂土的动弹性模量随频率增大呈对数曲线增长[9]。张向东等研究辽西地区冻风积土在地震荷载作用下的动力特性,在相同温度条件下,冻土的动剪切强度随着围压的增加而增加[10]。焦贵德等通过对-1 ℃的冻土试样在频率5 Hz的循环荷载下进行了单轴压缩试验,得出冻土滞回圈演化规律[11]。罗飞等对青藏黏土和兰州黄土进行分级加载,得出不同频率条件下,动弹性模量随动应变幅的增加最终趋于稳定,该稳定值随加载频率的增加而增大[12-13]。王丽霞等对冻土进行动静三轴试验,发现振次对动静强度有影响[14]。高志华等对含水量在50%的冻土开展不同温度,不同围压下的冻土动三轴试验,得出围压不同,动弹性模量与动应变的关系曲线不同[15]。
以上最大的不足是对冻土的动力学响应主要集中在低含冰量和振动荷载作用下,而西北寒区的冻土多为高含冰冻土,并且该地区为地震频发地区,所以迫切需要研究高含冰冻土在地震荷载作用下的动力学响应。本文的创新点是对兰州地区的高含冰量冻土进行逐级增加幅值动三轴试验,研究地震荷载作用下温度为-6,-3,-1.0 ℃,含水量为30%,50%,75%以及围压为0.3,0.5,1,2 MPa的高含冰量粉质黏土的动弹性模量。从试验中得到轴向动应变时程、轴向动应力时程及轴向动应力-动应变关系等试验关系曲线,推导出土样的动弹性模量,并分析各个变量对动弹性模量的影响,期望为寒区建设工程的抗震分析提供必要的高含冰量冻土参数依据。
1 试验条件
1.1 试验变量
本次试验主要研究温度、含水量和围压对高含冰量冻土动弹性模量的影响。温度在-5 ℃以上冻土的动力特性变化比较明显[16],又根据在《青藏铁路多年冻土区工程勘察暂行规定》[17],高温冻土区为0.0 ℃≥T≥-1 ℃;低温冻土区为T<-1 ℃,因此温度采用-3 ℃和-1 ℃,其中-1 ℃属于高温冻土,为了与-5 ℃以上冻土形成对比,也分析了-6 ℃冻土。马小杰等在做冻结黏土强度中发现,含水量在20%~40%,应力-应变曲线为软化型,含水量在60%~120%,应力-应变曲线为硬化型[18],因此本次含水量以50%为界,再取左右30%和75%的高含冰量冻土(含水量>20%为高含冰量冻土[19])作为含水量的变量。围压以试验仪器所能稳定控制的最小压强0.3 MPa开始,再选取0.5,1.0 MPa和2 MPa,主要探究低围压下冻土的动力特性。
1.2 加载方案
本次荷载为地震荷载,地震荷载与振动荷载不同之处在于振动荷载是往返循环荷载,而地震荷载是往复循环荷载,如图1所示,往复循环荷载的应力都大于初始应力。此次加载方案模拟7度地震烈度。按照Seed[20]等提出的方法:将随机地震波简化为一种等效谐波作用,谐波的幅值剪应力取τe<0.65τmax。则本试验中施加的动荷载为等效的、逐级增加幅值的、加卸荷载为周期变化的正弦波循环荷载,每级动荷载由最大动应力σ1max、最小动应力σ1min来确定。最大动应力σ1max、最小动应力σ1min是指在一个周期循环振动中应力所达到的最大和最小值,即正弦波的波峰与波谷。波峰与波谷根据试验围压不同而调整,然后对同一试样逐级增加动应力,共施加11级动荷载,直至试件破坏为止,表1为每级波峰和波谷参考数值。根据地震的烈度确定谐波的等效循环次数Ne为10次,即在每一级动应力作用下振动10次。振动频率都为1 Hz。
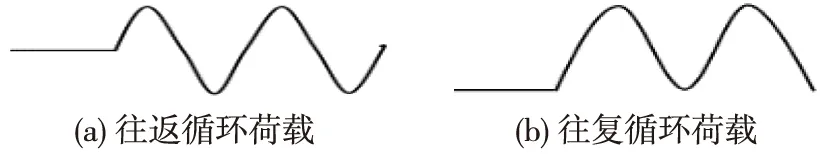
图1 冻土施加荷载

表1 每级施加的波峰和波谷单位应力kPa
2 试样制备及试验方法
兰州地区属于季节冻土区,气候寒冷,冬天平均气温在-9℃,位于黄河谷地,土质主要以碎砾土、粉质黏土和黄土为主,地处青藏高原地震区,抗震设防烈度为8度。选取兰州地区的粉质黏土作为试样用土,其天然含水量为13.24%,液限为32%,塑限为17.4%,粒度成分见表2。

表2 兰州粉质黏土的粒度成分
本次样品由于含水量较大,不能在常温条件下制样,制样过程是在冷冻库里进行的。为了消除外界温度的影响,在做试样之前,先将制样工具放进冷冻库制冷2h。制样的材料有3种,分别是土、冰以及水。土体的制样步骤为:烘干、碾碎、过筛(2 mm)、冷冻保存(图2)。冰通过粉碎机粉碎成2 mm的冰粒,放入冷冻箱保存(图3)。为了增加冰土之间的黏性,需要加少量冰水,使试样能够容易成形,不易破裂。在冷冻库里将土、冰和水按要求的比例混合,搅拌,捣鼓和挤压后成形(图4),成形后在两端放入环氧树脂帽,套进黑色的塑料薄膜,两端用橡皮圈固定,放入冷冻箱备用。

图2 制样土

图3 制样冰粒
室内冻土动三轴试验均在冻土工程国家重点实验室进行的,采用MTS-810型低温振动三轴材料试验机,频率范围为0~50 Hz,最大轴向负荷为100 kN,围压范围为0~22 MPa,温度范围为常温-30 ℃(图5)。在放入试样之前,要先将试样在试验温度下冷藏24 h。

图4 冻土样品

图5 MTS-810 试验机
3 试验结果及分析
3.1 冻土动应力应变关系
冻土动应力应变的曲线轮廓在不同条件下除幅值不一样外大致相同,图6是温度在-6 ℃,含水量在30%,围压0.3 MPa的情况下冻土动应力-应变关系曲线。其中,应力水平为1.63~1.94 MPa,2.22~2.36 MPa和2.32~2.73 MPa的动应力-应变关系曲线如图7所示。从图6和图7可以看出,冻土应力随着应变呈阶梯式增长,随着应变增加,应力-应变关系曲线向双曲线趋势发展,符合Hardin-Drnevich双曲线模型,见式(1)或者式(2)(以下简称H-D模型)。
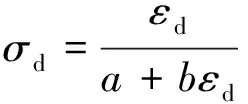
(1)
或
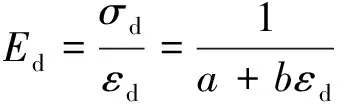
(2)
式中,σd、εd分别为各个时刻的动应力和动应变;a、b为试验参数。
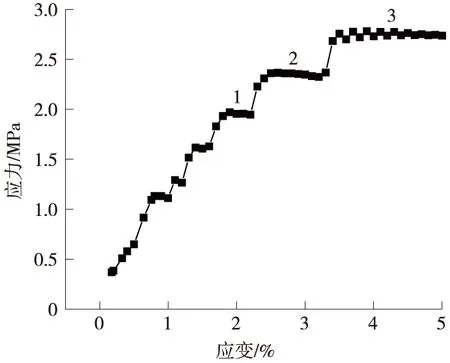
图6 冻土动应力-应变关系曲线
为了更好地说明冻土的动应力-应变关系符合H-D模型,对图6编号的1、2和3曲线进行验证。根据公式(2),得出式(3)

(3)
根据公式(3)可对编号1、2和3曲线进行线性拟合,拟合结果见图8和表3。
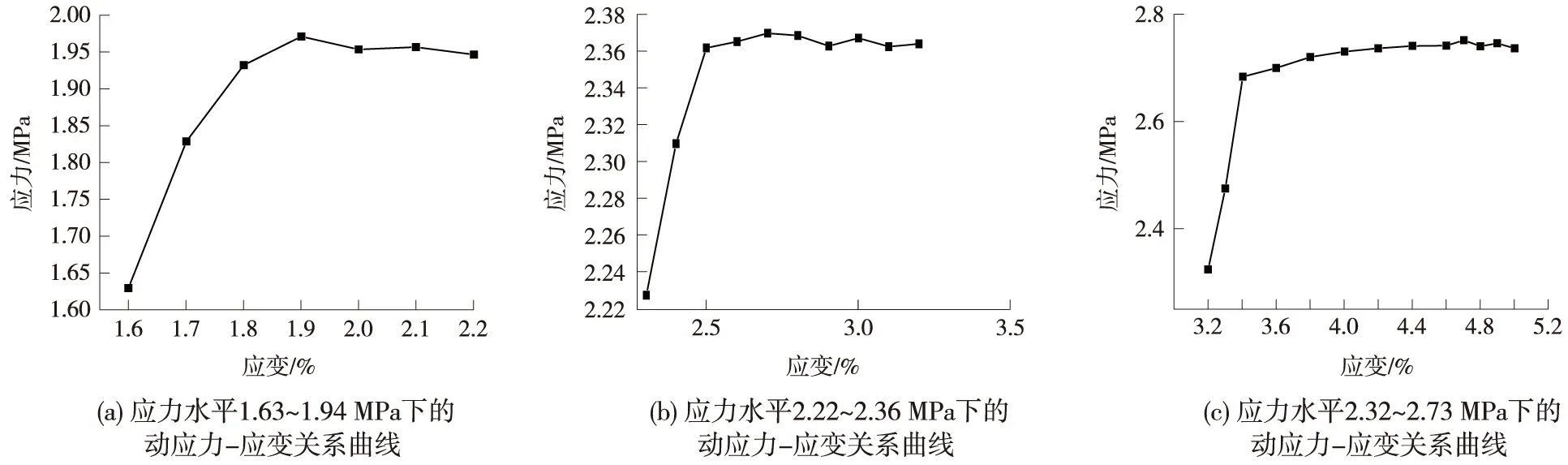
图7 编号1、2和3动应力-应变关系
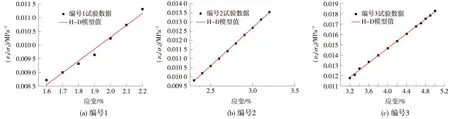
图8 编号1、2和3的试验数据和H-D模型值对比

表3 编号1、2和3的参数拟合结果
从图8和表3可以看出,随着应变的增加,试验数据与H-D模型值逐渐吻合,且R2逐渐增大,拟合相关系数R2均大于0.98,则说明应变大时,冻土的应力应变符合H-D双曲线模型。从表3也可以看出,b值会随着应力增大逐渐减小。
H-D模型参数即a和b,是与温度、围压和含水量有关的参数,研究H-D模型参数与温度、围压和含水量的关系有助于对冻土的本构模型有更清晰的认识,也为抗震设计的数值模拟提供材料参数。
从式(1)可以看出,当εd趋近于无限大时,最大动应力σd趋于1/b,从式(2)可以看出当εd趋近于 0 时,最大动弹性模量E趋于1/a。从这可以看出a和b的物理意义。
下面将研究H-D模型拟合参数在不同条件下的变化。
3.1.1 温度对H-D双曲线模型参数的影响
从图9和表4可以看出,随着温度的升高,H-D模型参数a和b都随之增大,并且在高温-1 ℃时,a和b值明显大于其他两个温度所对应的参数。
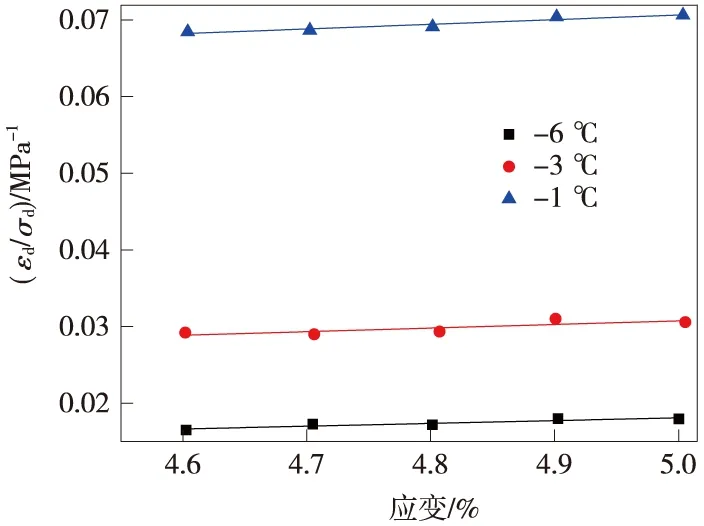
图9 不同温度下H-D模型拟合

温度abR2-6℃5.2×10-43.51×10-30.98184-3℃1.69×10-37.23×10-30.99589-1℃8.36×10-31.528×10-20.98151
3.1.2 围压对H-D双曲线模型参数的影响
由表4可知,在-1 ℃时,H-D模型参数a和b增加幅度较大,所以选取-1 ℃时不同围压的H-D模型参数进行比较(含水量同)。从图10和表5可以看出,H-D模型参数b值随围压变化在0.01~0.015浮动。
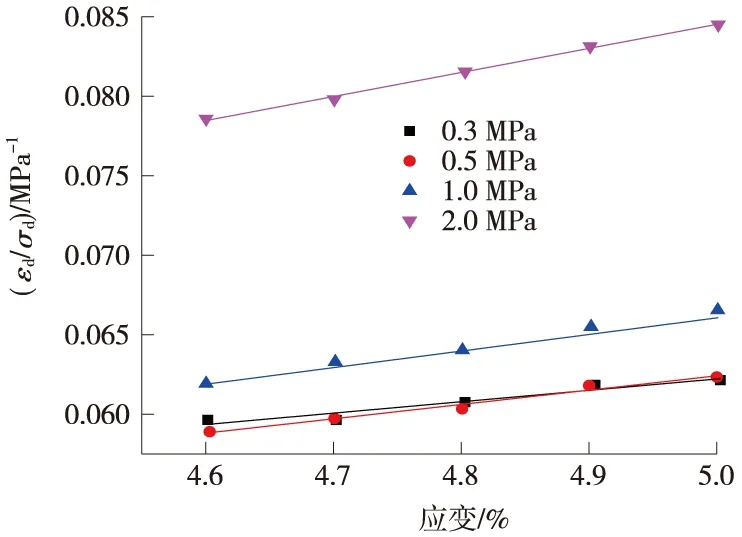
图10 不同围压下H-D模型拟合

围压abR20.3MPa8.59×10-31.086×10-20.99630.5MPa8.87×10-31.513×10-20.996421MPa9.4×10-31.143×10-20.990342MPa1.87×10-21.513×10-20.99642
3.1.3 含水量对H-D双曲线模型参数的影响
从图11和表6可以看出,对H-D模型参数b来说,b在含水量50% 最小,并且b值随着含水量增大先减小后增大。
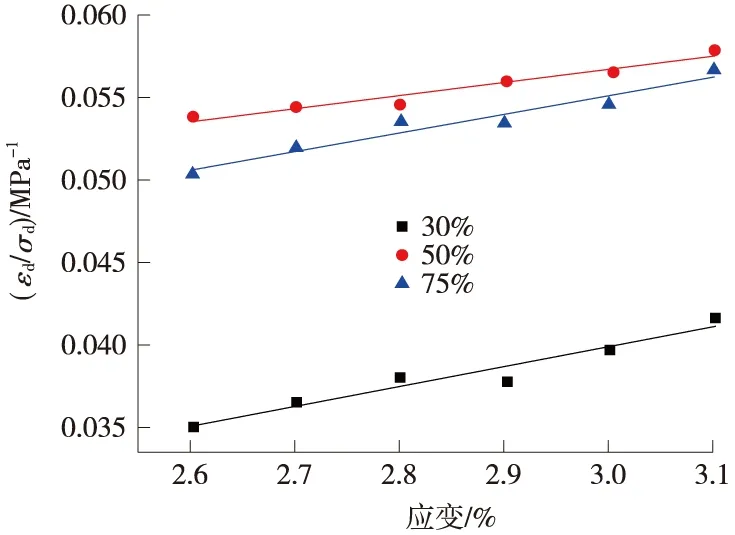
图11 不同含水量下H-D模型拟合

含水量abR230%1.336×10-21.694×10-20.9825250%3.277×10-28.03×10-30.9839275%2.312×10-21.073×10-20.98186
3.2 动弹性模量
动弹性模量是研究冻土动力特性的重要参数之一。因为施加的是动荷载,所以应力和应变是属于时间的函数,而冻土应力应变关系具有非线性,则弹性模量也是随时间变化。
通过H-D模型方程的转换,可得动弹性模量与应变之间的关系。由公式(2)可知动弹性模量可表示为式(4)
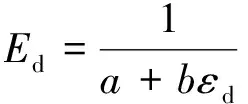
(4)
3.2.1 温度对动弹性模量的影响
温度是影响冻土的动力特性重要因数之一。图12是不同温度下(含水量50%、围压0.3 MPa)动弹性模量随应变的变化,可以看出温度在-6 ℃时,弹性模量在134.5~55.7 MPa,温度在-3 ℃时,弹性模量在82.2~32.7 MPa,温度在-1 ℃时,弹性模量在42.3~14.2 MPa,温度每升高1度,弹性模量下降12~15 MPa。在同含水量和围压的情况下,温度越高,动弹性模量越小。这个不难理解,温度越高,冻土的未冻水越多,导致冻土强度越小,从而使动弹性模量越小。
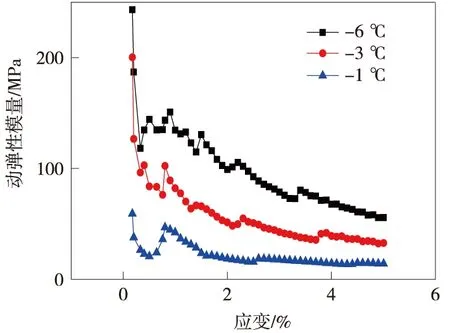
图12 不同温度下动弹性模量随应变的变化
3.2.2 围压对动弹性模量的影响
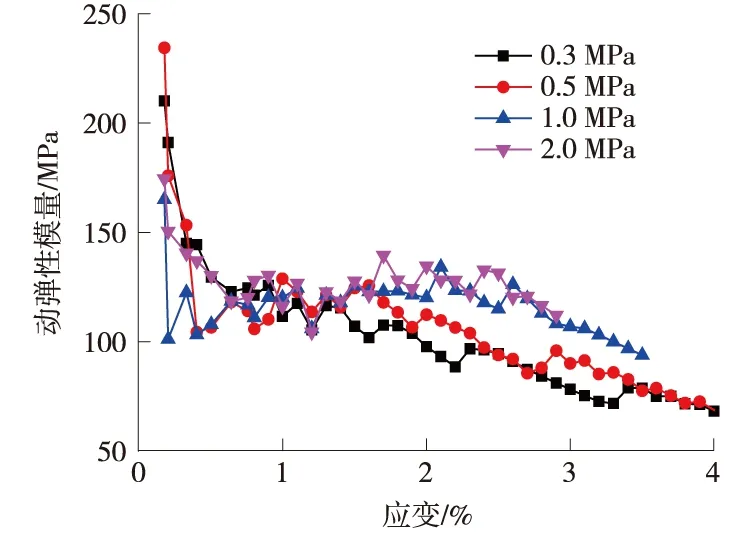
图13 不同围压下动弹性模量随应变的变化(-6 ℃)
图13是在-6 ℃情况下不同围压的动弹性模量随应变的变化,从图13可以看出,温度在-6 ℃时,围压越大,动弹性模量越大。图14是在-1 ℃情况下不同围压的动弹性模量随应变的变化,从图14可以看出,温度在-1 ℃时,应变小的时候(试验刚开始),围压越大,动弹性模量越大,但是应变逐渐增大时,发现围压越大,其动弹性模量有减小的趋势。分析其机理,可知围压对冻土起到两个作用,一个是对冻土的强度有强化作用,一个是对冻土起到破坏作用。强化作用是指围压对冻土增加了侧向约束,从而增加了冻土的强度,弱化作用是指围压充当破坏荷载,高压下使孔隙冰融化,使土承受荷载,从而使冻土强度减少。一般情况下,围压对冻土的影响是强化起主导作用,但在-1 ℃下,孔隙冰更容易融化,使土颗粒之间有润滑作用,从而弱化更为明显。
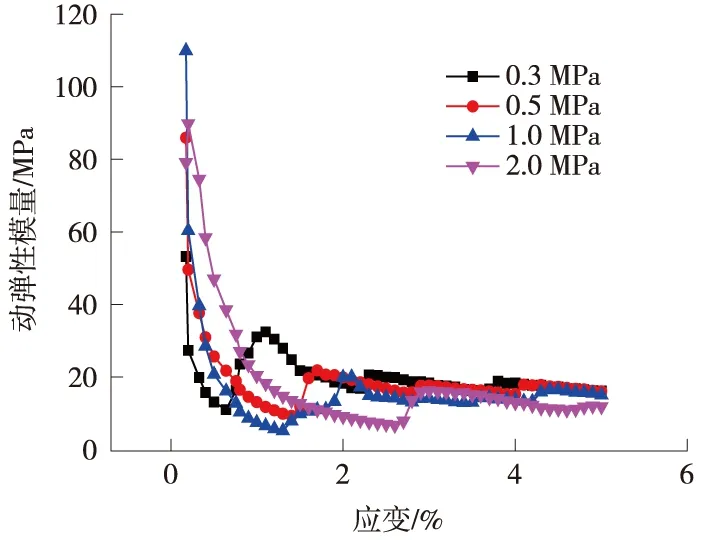
图14 不同围压下动弹性模量随应变的变化(-1 ℃)
3.2.3 含水量对动弹性模量的影响
图15是在-6 ℃情况下不同含水量的动弹性模量随应变的变化。从图15可以看出,含水量在50%时有最小的趋势,而从图16在-1 ℃情况下就可以很明显看出含水量在50%时,其动弹性模量最小。所以从图15和图16可以总结出,动弹性模量在含水量30%~50%之间是减少的,在含水量50%~75%之间是增加的。从冻土的机理可以分析出,在高含冰量冻土,其含水量已达到饱和含水量,含水率再增大,土颗粒骨架被撑开,胶结作用减弱,其动弹性模量减少;含水率进一步增大,土的强度主要体现冰的强度,冰含量增大使动弹性模量又增大。因此在不同含水量的高含冰量冻土存在一个最差含水量,其弹性模量最小。

图15 不同含水量下动弹性模量随应变的变化(-6 ℃)
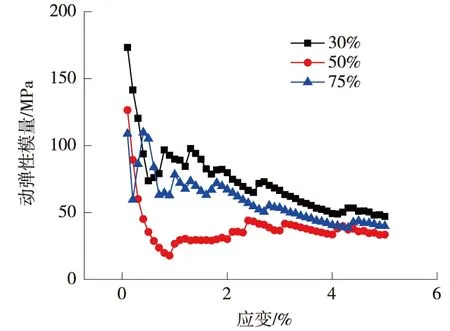
图16 不同含水量下动弹性模量随应变的变化(-1 ℃)
4 结论
(1)高含冰量冻土在幅值增加的正弦波循环荷载下,应力应变呈阶梯式增长,应变大时阶梯呈Hardin-Drnevich双曲线模型分布,即σd=εd/(a+bεd),并且温度、围压和含水量都对模型参数有着影响。
(2)地震荷载下,相同含水量和围压下,温度越大,土体的动弹性模量越小,并且温度每升高1 ℃,弹性模量下降12~15 MPa。
(3)地震荷载下围压对高含冰量冻土有强化作用和弱化作用,在-6 ℃温度时,围压越大,强化作用较大,动弹性模量增大;在-1 ℃温度时,应变量小时,围压对高含冰量冻土的影响跟-6 ℃相同,应变量大时,围压越大,弱化作用较大,动弹性模量减小。
(4)对于试验所作的高含冰量冻土,其含水量已经超过饱和含水量,地震荷载下含水量对高含冰量冻土的影响是先随含水量(30%~50%)增大而减小,再随含水量(50%~75%)增大而增大,因此存在一个最差含水量,其弹性模量最小。
(5)通过对比可知,温度对高含冰量冻土的影响远远大于围压和含水量对高含冰量冻土的影响,因此在选取抗震设计中的冻土参数时应先确定冻土温度。
