基于傅里叶级数的防伪扭索曲线设计∗
2019-11-29夏自由
夏自由
(长沙师范学院 长沙 410100)
1 引言
扭索曲线是版纹防伪的基本要素。扭索曲线在防伪底纹制作上得到广泛应用。我国2005 年版、2015年版百元钞票都采用了扭索曲线进行防伪。
在版纹防伪设计软件中,扭索曲线主要通过数学函数生成,以正弦函数、余弦函数为主。曲线光滑、对称、美观,常规图形设计软件无法绘制出来,具有一定的防伪性,同时可对正(余)弦函数进行线性运算,改变曲线的形状,提升扭索曲线的防伪性能[1~4]。
2 傅里叶级数理论
根据傅里叶级数理论,周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示,如式(1)所示[5~6]。
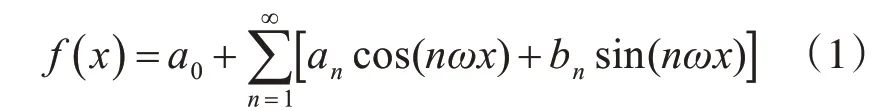
反过来,用有限项傅里叶级数可构建周期函数,生成扭索曲线,曲线的波形为各单项函数的谐波之和[7~11]。
采用傅里叶级数公式建立的曲线光滑、美观,而且具有一定的周期性,适合制作防伪扭索曲线。而且,曲线形状随傅里叶级数中单项函数的幅值变化而变化,曲线的防伪效果好,仿造者如没有破解复合函数的参数,就无法仿制出曲线。因此,傅里叶级数公式适用于防伪扭索曲线设计[12~18]。
3 实验
采用傅里叶级数公式设计扭索曲线时,为了保证曲线的美观度,需要按照一定的规律来构建复合函数。本研究采用Cerber3.0 防伪版纹设计软件进行实验,探寻复合函数构建中,谐波分量、级数对曲线形状的影响。
Cerber3.0为俄罗斯开发的防伪版纹设计软件,可基于图形界面构建二维傅里叶级数复合函数。如图1所示。

图1 Cerber3.0中傅里叶级数复合函数的构建
谐波AB 表示Y 轴方向傅里叶级数的各单项函数的幅值,对应式(2)。谐波CD 表示X轴方向傅里叶级数的各单项函数的幅值,对应式(3)。
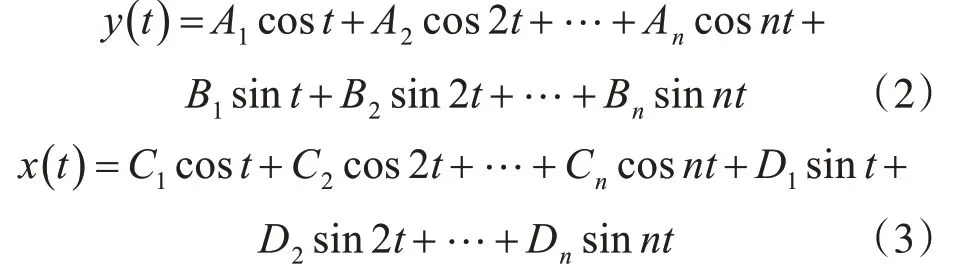
构建复合函数时,谐波A、B、C、D 的值采取相对值方式,大小范围为-10~10,级数n 的范围为0~255 级。设置好复合函数的参数后,就可生成对应的扭索曲线。
3.1 Y轴方向构建复合函数
Y 轴方向,基于公式(2)构建复合函数,曲线的波形沿着Y轴方向进行谐波变换。如图2所示。


图2 Y轴方向复合函数的曲线形状
从图3 中可以看出,当级数为1 时,可生成正(余)弦曲线;当级数为2 时,可生成双频干涉扭索曲线;随着级数的增加,曲线的形状变得复杂。
在实际应用中,为了保持曲线的美观,需要按照一定的原则设置n、A、B的值。有以下几个原则:
1)级数n 决定一个周期内Y 轴方向波峰的数量,最多波峰数量与n值相等。
2)调整A、B值,会改变曲线波峰、波谷的形状、位置。
3)当B 取值都为0 时,复合函数都是由余弦函数构成,形成的函数曲线具有左右对称性。如图3所示。
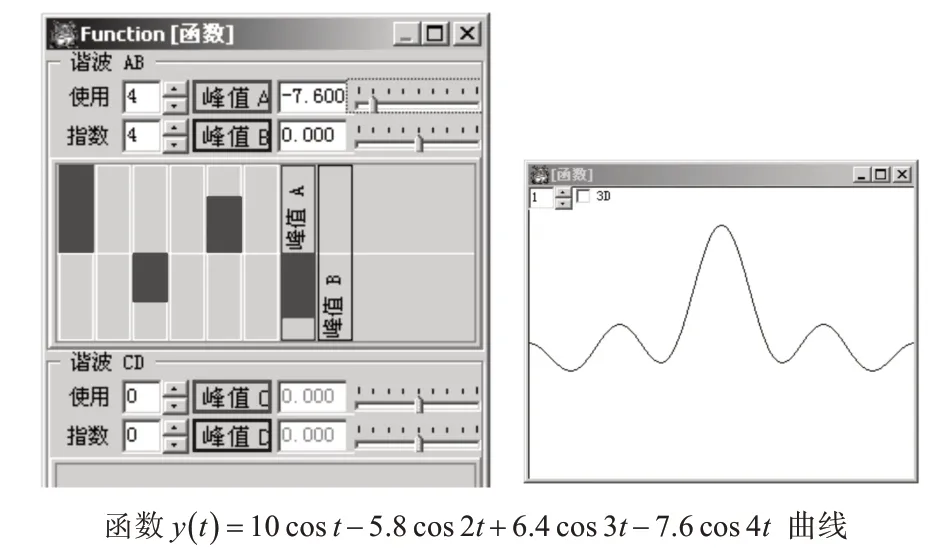
图3 B=0,复合函数的曲线左右对称
3.2 X轴方向构建复合函数
X 轴方向,基于式(3)构建复合函数,曲线的波形沿着X轴方向进行谐波变换。如图4所示。


图4 X轴方向复合函数调整曲线形状
从图4 中可以看出,调整C、D 值,曲线波形出现倾斜、交错的效果。在实际应用中,为了保持曲线的美观,需要按照一定的原则设置n、C、D 的值。有以下几个原则:
1)级数n 决定一个周期内X 轴方向波峰的数量,最多波峰数量与n 值相等。另外,如果曲线形成交错效果时,最多的交错次数也与n值相等。
2)调整C、D 值,曲线在X 轴方向进行谐波变换,即曲线沿着X轴方向出现倾斜或变形。
3)当D 取值为0 时,式(3)中的复合函数都是由余弦函数构成,形成的波形曲线具有上下旋转对称性。如图5所示。
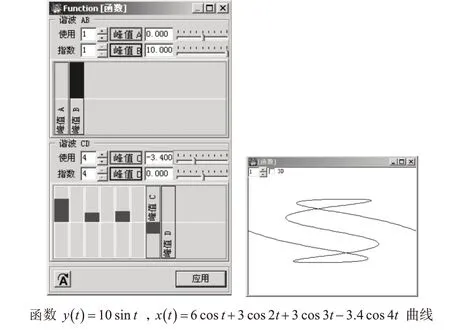
图5 D=0,复合函数的曲线上下旋转对称
3.3 二维方向构建复合函数
在X轴、Y轴方向同时构建复合函数时,曲线在X轴方向、Y轴方向同时进行谐波变换,形状变得复杂。如图6所示。
4 结果分析
根据以上分析,利用傅里叶级数公式,可以复合出复杂的三角函数,对应的扭索曲线复杂,仿制难度非常大,同时又具有周期性,适合用于防伪底纹的制作。但设计制作防伪底纹时,还需要考虑底纹的美观因素,因此并不是任意复合函数都适用于扭索曲线的设计。综合考虑,利用傅里叶级数公式制作扭索曲线时,以下设计经验值得借鉴。
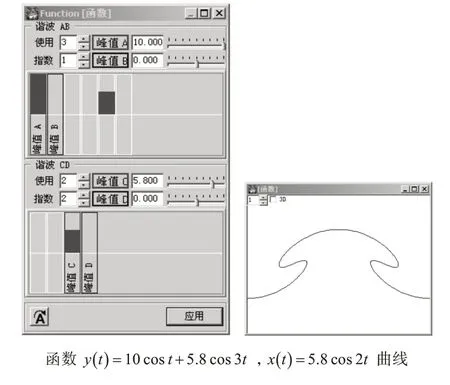
图6 二维方向构建复合函数形成的曲线
1)构建的复合函数时,使用的级数越多,生成曲线越复杂,防伪效果越好,但级数增加,一方面会增加计算的时间,软件处理速度变慢,另一方面,值越大,调整意图具有盲目性,效果也无法控制,导致曲线形状过于复杂,影响版纹的美观度。当Y 轴方向达到4 级,X 轴方向达到2 级时,曲线被反向分解破解的难度已经较大,生成的曲线较为美观。
2)构建复合函数时,谐波B、D 的值设置为0,只调整A 值、C 值,扭索曲线具有对称性,制作的底纹美观度高。
3)利用傅里叶级数公式建立的复合函数,曲线形状各异,但并不是所有的曲线都适用于制作防伪版纹,因为还要考虑版纹的美观性。生产应用中,可以通过实验选择适合的复合函数来制作扭索曲线。图7为复合函数曲线制作的防伪底纹效果。
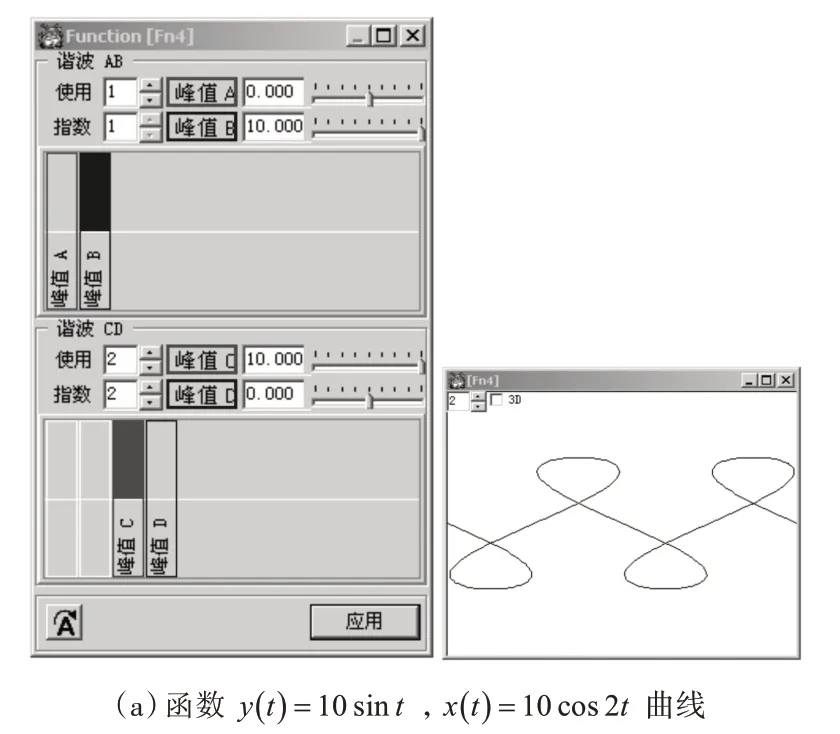
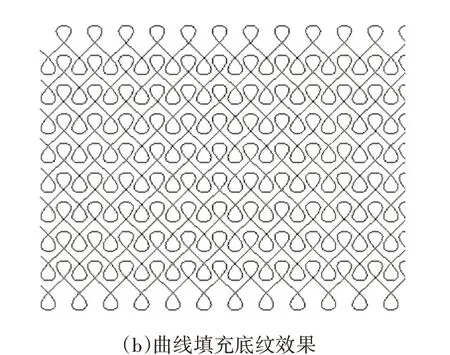
图7 复合函数曲线及底纹填充效果
5 结语
利用傅里叶级数公式设计防伪扭索曲线时,需要把防伪性能与美观度结合起来。复合函数的参数简单,造假者容易破解参数,仿制出版纹;复合函数参数复杂,曲线形状变得复杂,版纹的美观度降低。因此,设计时需要综合考虑,平衡处理。
